查找最小生成树：克鲁斯克尔算法（Kruskal）算法

一、算法介绍

　　Kruskal算法是一种用来查找最小生成树的算法，由Joseph Kruskal在1956年发表。用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪心算法的应用。和Boruvka算法不同的地方是，Kruskal 算法在图中存在相同权值的边时也有效。最小生成树是一副连通加权无向图中一棵权值最小的生成树（minimum spanning tree，简称MST）。生成树的权重是赋予生成树的每条边的权重之和。最小生成树具有 (V – 1) 个边，其中 V 是给定图中的顶点数。关于最小生成树，它可以应用在网络设计、NP难题之类的问题，还可以用于聚类分析，还可以间接应用于其他问题。

二、Kruskal算法查找MST的步骤

1. 按权重的顺序方式来对所有边进行排序。

2. 选择权重最小的边。检查它是否与形成的生成树形成一个循环。如果未形成循环，则包括该边。否则，将其丢弃。

3. 重复步骤2，直到生成树中有（V-1）个边。

　　这个算法是贪婪算法。“贪婪的选择”是选择迄今为止不会造成MST成环的最小的权重边。下面来一个例子来理解：

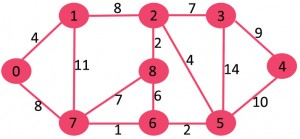
　　该图包含9个顶点（V）和14个边（E）。因此，形成的最小生成树将具有（9 – 1）= 8 个边。

　　步骤1：每条边按顺序来排序

 1     　　/**
 2          * 排序后：
 3          * 权重-src-dest
 4          * 1 6 7
 5          * 2 2 8
 6          * 2 5 6
 7          * 4 0 1
 8          * 4 2 5
 9          * 6 6 8
10          * 7 2 3
11          * 7 7 8
12          * 8 0 7
13          * 8 1 2
14          * 9 3 4
15          * 10 4 5
16          * 11 1 7
17          * 14 3 5
18          */

　　步骤2+步骤3：：利用按权重排好序的边数组，每次选取最小边，并检测是否成环。MST不能有环，所以这里涉及一个并查集的概念，并查集是对这个 Kruskal 算法进行优化的。

　　1）数组中一个接一个地选取所有边。选取边6-7：不形成循环，将其包括在内。

　　2）选取边2-8：不形成循环，将其包括在内。

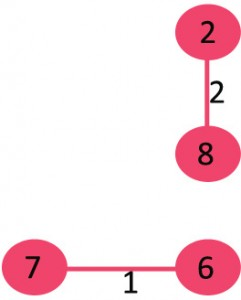
　　3）选取边5-6：不形成循环，将其包括在内。

　　4）选取边0-1：不形成循环，将其包括在内。

　　5）选取边2-5：不形成循环，将其包括在内。

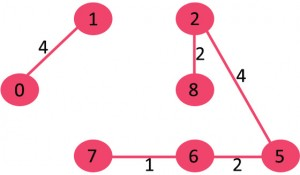
　　6）选取边6-8：由于包括该边会导致成环，因此将其丢弃。

　　7）选取边2-3：不形成循环，将其包括在内。

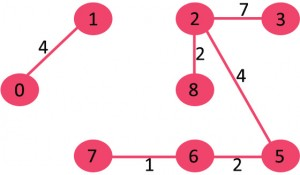
　　8）选取边7-8：由于包括该边会导致循环，因此请将其丢弃。

　　9）选取边0-7：不形成循环，将其包括在内。

　  10）选取边1-2：由于包括该边会导致循环，因此请将其丢弃。

　   11）选取边3-4：不形成循环，将其包括在内。

　　由于包含的边数等于（V – 1），因此算法结束。

三、算法代码

并查集：

　　在计算机科学中，并查集是一种树型的数据结构，用于处理一些不交集（Disjoint Sets）的合并及查询问题。有一个联合-查找算法（union-find algorithm）定义了两个用于此数据结构的操作：

• Find：确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。

• Union：将两个子集合并成同一个集合。

　　并查集树是一种将每一个集合以树表示的数据结构，其中每一个节点保存着到它的父节点的引用。

　　在并查集树中，每个集合的代表即是集合的根节点。“查找”根据其父节点的引用向根行进直到到底树根。“联合”将两棵树合并到一起，这通过将一棵树的根连接到另一棵树的根。实现这样操作的一种方法是：

　　查找元素 i 的集合，根据其父节点的引用向根行进直到到底树根：

1     private int find(Subset[] subsets, int i) {
2         if (subsets[i].parent != i)
3             subsets[i].parent = find(subsets, subsets[i].parent);   // 路径压缩，找到最久远的祖先时“顺便”把它的子孙直接连接到它上面
4         return subsets[i].parent;
5     }

　　将两组不相交集合 x 和 y 进行并集，找到其中一个子集最父亲的父亲（也就是最久远的祖先），将另外一个子集的最久远的祖先的父亲指向它：

 1     public void union(Subset[] subsets, int x, int y) {
 2         int xroot = find(subsets, x);
 3         int yroot = find(subsets, y);
 4
 5         /* 在高秩树的根下附加秩低树（按秩划分合并） */
 6         if (subsets[xroot].rank < subsets[yroot].rank) {
 7             subsets[xroot].parent = yroot;
 8         } else if (subsets[xroot].rank > subsets[yroot].rank){
 9             subsets[yroot].parent = xroot;
10         } else {    // 当两棵秩同为r的树联合(作并集)时，它们的秩r+1
11             subsets[yroot].parent = xroot;
12             subsets[xroot].rank++;
13         }
14     }

　　同时使用路径压缩、按秩（rank）合并优化的程序每个操作的平均时间仅为 O(α (n))，其中α (n) 是 n=f(x)=A(x, x) 的反函数，A 是急速增加的阿克曼函数。因为 α(n) 是其反函数，故 α (n) 在 n 十分巨大时还是小于 5。因此，平均运行时间是一个极小的常数。实际上，这是渐近最优算法。

Kruskal算法

　　使用算法的思想来构造MST。

 1     /**
 2      * 使用Kruskal算法构造MST
 3      */
 4     public void kruskalMST() {
 5         Edge[] result = new Edge[V]; // 将存储生成的MST
 6         int e = 0;                   // 用于result[]的索引变量
 7         int i = 0;                   // 用于排序的边缘索引变量
 8         for (i = 0; i < V; ++i) {
 9             result[i] = new Edge();
10         }
11
12         /* 步骤一：对点到点的边的权重进行排序 */
13         Arrays.sort(edges);
14
15         /* 创建V个子集*/
16         Subset[] subsets = new Subset[V];
17         for (i = 0; i < V; i++) {
18             subsets[i] = new Subset();
19         }
20
21         /* 使用单个元素创建V子集 */
22         for (int v = 0; v < V; v++) {
23             subsets[v].parent = v;
24             subsets[v].rank = 0;    // 单元素的树的秩定义为0
25         }
26
27         /* 用于挑选下一个边的索引 */
28         i = 0;
29
30         while (e < V-1) {
31             /* 步骤2：选取最小的边缘, 并增加下一次迭代的索引 */
32             Edge next_edge = edges[i++];
33
34             int x = find(subsets, next_edge.src);
35             int y = find(subsets, next_edge.dest);
36
37             /* 如果包括此边不引起mst成环（树本无环），则将其包括在结果中并为下一个边增加结果索引存下一条边 */
38             /* 这里判断两个元素是否属于一个子集 */
39             if (x != y) {
40                 result[e++] = next_edge;
41                 union(subsets, x, y);
42             }
43             /* 否则丢弃next_edge */
44         }
45
46         /* 打印result[]的内容以显示里面所构造的MST */
47         System.out.println("Following are the edges in the constructed MST");
48         for (i = 0; i < e; ++i) {
49             System.out.println(result[i].src + " -- " + result[i].dest + " == " + result[i].weight);
50         }
51     }

　　平均时间复杂度为O (|E|·log |V|)，其中 E 和 V 分别是图的边集和点集。

本文源代码：

  1 package algorithm.mst;
  2
  3 import java.util.Arrays;
  4
  5 public class KruskalAlgorithm {
  6     /* 顶点数和边数 */
  7     private int V, E;
  8     /* 所有边的集合 */
  9     private Edge[] edges;
 10
 11     /**
 12      * 创建一个V个顶点和E条边的图
 13      *
 14      * @param v
 15      * @param e
 16      */
 17     public KruskalAlgorithm(int v, int e) {
 18         V = v;
 19         E = e;
 20         edges = new Edge[E];
 21         for (int i = 0; i < e; i++) {
 22             edges[i] = new Edge();
 23         }
 24     }
 25
 26     /**
 27      * 查找元素i的集合（路径压缩）
 28      * 根据其父节点的引用向根行进直到到底树根
 29      *
 30      * @param subsets
 31      * @param i
 32      * @return
 33      */
 34     private int find(Subset[] subsets, int i) {
 35         if (subsets[i].parent != i)
 36             subsets[i].parent = find(subsets, subsets[i].parent);   // 路径压缩，找到最久远的祖先时“顺便”把它的子孙直接连接到它上面
 37         return subsets[i].parent;
 38     }
 39
 40     /**
 41      * 将两组不相交集合x和y进行并集（按秩合并）
 42      * 这个方法找到其中一个子集最父亲的父亲（也就是最久远的祖先），将另外一个子集的最久远的祖先的父亲指向它。
 43      * <p>
 44      *     并查集树的最基础的表示方法，这个方法不会比链表法好，
 45      *     这是因为创建的树可能会严重不平衡。
 46      *     所以采用“按秩合并”来优化。
 47      * </p>
 48      * <p>
 49      *     即总是将更小的树连接至更大的树上。因为影响运行时间的是树的深度，
 50      *     更小的树添加到更深的树的根上将不会增加秩除非它们的秩相同。
 51      *     在这个算法中，术语“秩”替代了“深度”，因为同时应用了路径压缩时秩将不会与高度相同。
 52      * </p>
 53      *
 54      * @param subsets
 55      * @param x
 56      * @param y
 57      */
 58     public void union(Subset[] subsets, int x, int y) {
 59         int xroot = find(subsets, x);
 60         int yroot = find(subsets, y);
 61
 62         /* 在高秩树的根下附加秩低树（按秩划分合并） */
 63         if (subsets[xroot].rank < subsets[yroot].rank) {
 64             subsets[xroot].parent = yroot;
 65         } else if (subsets[xroot].rank > subsets[yroot].rank){
 66             subsets[yroot].parent = xroot;
 67         } else {    // 当两棵秩同为r的树联合(作并集)时，它们的秩r+1
 68             subsets[yroot].parent = xroot;
 69             subsets[xroot].rank++;
 70         }
 71     }
 72
 73     /**
 74      * 使用Kruskal算法构造MST
 75      */
 76     public void kruskalMST() {
 77         Edge[] result = new Edge[V]; // 将存储生成的MST
 78         int e = 0;                   // 用于result[]的索引变量
 79         int i = 0;                   // 用于排序的边缘索引变量
 80         for (i = 0; i < V; ++i) {
 81             result[i] = new Edge();
 82         }
 83
 84         /* 步骤一：对点到点的边的权重进行排序 */
 85         Arrays.sort(edges);
 86
 87         /* 创建V个子集*/
 88         Subset[] subsets = new Subset[V];
 89         for (i = 0; i < V; i++) {
 90             subsets[i] = new Subset();
 91         }
 92
 93         /* 使用单个元素创建V子集 */
 94         for (int v = 0; v < V; v++) {
 95             subsets[v].parent = v;
 96             subsets[v].rank = 0;    // 单元素的树的秩定义为0
 97         }
 98
 99         /* 用于挑选下一个边的索引 */
100         i = 0;
101
102         while (e < V-1) {
103             /* 步骤2：选取最小的边缘, 并增加下一次迭代的索引 */
104             Edge next_edge = edges[i++];
105
106             int x = find(subsets, next_edge.src);
107             int y = find(subsets, next_edge.dest);
108
109             /* 如果包括此边不引起mst成环（树本无环），则将其包括在结果中并为下一个边增加结果索引存下一条边 */
110             /* 这里判断两个元素是否属于一个子集 */
111             if (x != y) {
112                 result[e++] = next_edge;
113                 union(subsets, x, y);
114             }
115             /* 否则丢弃next_edge */
116         }
117
118         /* 打印result[]的内容以显示里面所构造的MST */
119         System.out.println("Following are the edges in the constructed MST");
120         for (i = 0; i < e; ++i) {
121             System.out.println(result[i].src + " -- " + result[i].dest + " == " + result[i].weight);
122         }
123     }
124
125     public static void main(String[] args) {
126         /**
127          * 排序后：
128          * 权重-src-dest
129          * 1 6 7
130          * 2 2 8
131          * 2 5 6
132          * 4 0 1
133          * 4 2 5
134          * 6 6 8
135          * 7 2 3
136          * 7 7 8
137          * 8 0 7
138          * 8 1 2
139          * 9 3 4
140          * 10 4 5
141          * 11 1 7
142          * 14 3 5
143          */
144         int V = 9;
145         int E = 14;
146         KruskalAlgorithm graph = new KruskalAlgorithm(V, E);
147
148         /* 另一个用例的图:
149               1 --- 2 --- 3
150             / |     | \   | \
151            0  |     8  \  |  4
152             \ |  /  |   \ | /
153               7 --- 6 --- 5
154          */
155
156         // 添加边 0-1
157         graph.edges[0].src = 0;
158         graph.edges[0].dest = 1;
159         graph.edges[0].weight = 4;
160
161         // 添加边 0-7
162         graph.edges[1].src = 0;
163         graph.edges[1].dest = 7;
164         graph.edges[1].weight = 8;
165
166         // 添加边 1-2
167         graph.edges[2].src = 1;
168         graph.edges[2].dest = 2;
169         graph.edges[2].weight = 8;
170
171         // 添加边 1-7
172         graph.edges[3].src = 1;
173         graph.edges[3].dest = 7;
174         graph.edges[3].weight = 11;
175
176         // 添加边 2-3
177         graph.edges[4].src = 2;
178         graph.edges[4].dest = 3;
179         graph.edges[4].weight = 7;
180
181         // 添加边 2-5
182         graph.edges[5].src = 2;
183         graph.edges[5].dest = 5;
184         graph.edges[5].weight = 4;
185
186         // 添加边 2-8
187         graph.edges[6].src = 2;
188         graph.edges[6].dest = 8;
189         graph.edges[6].weight = 2;
190
191         // 添加边 3-4
192         graph.edges[7].src = 3;
193         graph.edges[7].dest = 4;
194         graph.edges[7].weight = 9;
195
196         // 添加边 3-5
197         graph.edges[8].src = 3;
198         graph.edges[8].dest = 5;
199         graph.edges[8].weight = 14;
200
201         // 添加边 4-5
202         graph.edges[9].src = 4;
203         graph.edges[9].dest = 5;
204         graph.edges[9].weight = 10;
205
206         // 添加边 5-6
207         graph.edges[10].src = 5;
208         graph.edges[10].dest = 6;
209         graph.edges[10].weight = 2;
210
211         // 添加边 6-7
212         graph.edges[11].src = 6;
213         graph.edges[11].dest = 7;
214         graph.edges[11].weight = 1;
215
216         // 添加边 6-8
217         graph.edges[12].src = 6;
218         graph.edges[12].dest = 8;
219         graph.edges[12].weight = 6;
220
221         // 添加边 7-8
222         graph.edges[13].src = 7;
223         graph.edges[13].dest = 8;
224         graph.edges[13].weight = 7;
225
226         graph.kruskalMST();
227
228         /* 用例通过算法得出的MST如下:
229                1    2 -- 3
230              /      | \   \
231             0       8  \   4
232              \          \
233                7 -- 6 -- 5
234          */
235     }
236
237     /**
238      * 每条边的信息，实现了{@link Comparable}接口,
239      *      可以使用{@link Arrays}的方法随其边的权重的集合进行自然排序。
240      */
241     class Edge implements Comparable<Edge> {
242         /* 这条边的两个顶点和它的权重 */
243         private int src, dest, weight;
244
245         @Override
246         public int compareTo(Edge o) {
247             return this.weight - o.weight;
248         }
249     }
250
251     /**
252      * 联合查找子集的类
253      */
254     class Subset {
255         /* 其祖先和秩 */
256         private int parent, rank;
257     }
258 }