LeetCode：堆专题

堆专题

参考了力扣加加对与堆专题的讲解，刷了些 leetcode 题，在此做一些记录，不然没几天就忘光光了

力扣加加-堆专题(上)

力扣加加-堆专题(下)

总结

优先队列

// 1.java中有优先队列的实现：默认是小顶堆
PriorityQueue<Integer> minHeap = new PriorityQueue<>(3);

maxHeap.offer(1);
maxHeap.offer(2);
maxHeap.offer(3);

System.out.println(maxHeap.poll());  // 1
System.out.println(maxHeap.poll());  // 2
System.out.println(maxHeap.poll());  // 3

// 2.修改一下：变成大顶堆
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(3, (a, b) -> b-a);
// 或者
// PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b-a);

// 3.构造函数如下：
public PriorityQueue(int initialCapacity,
                     Comparator<? super E> comparator) {
    // Note: This restriction of at least one is not actually needed,
    // but continues for 1.5 compatibility
    if (initialCapacity < 1)
        throw new IllegalArgumentException();
    this.queue = new Object[initialCapacity];
    this.comparator = comparator;
}

一个中心

动态求极值

而求极值无非就是最大值或者最小值，这不难看出。如果求最大值，我们可以使用大顶堆，如果求最小值，可以用最小堆。

而实际上，如果没有动态两个字，很多情况下没有必要使用堆。比如可以直接一次遍历找出最大的即可。而动态这个点不容易看出来，这正是题目的难点。这需要你先对问题进行分析， 分析出这道题其实就是动态求极值，那么使用堆来优化就应该被想到。

• 1046. 最后一块石头的重量
• 263. 丑数、264. 丑数 II、313. 超级丑数

两种实现

基于链表的实现——跳表

也是一种数据结构，1206. 设计跳表

待做，估计是不会去做了

基于数组的实现——二叉堆

核心的两个操作就是：出堆/入堆

基本原理

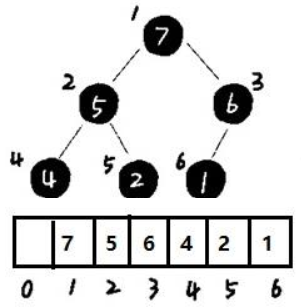
本质上，二叉堆就是一颗特殊的完全二叉树，父节点的权值不小于儿子的权值（大顶堆），即根节点就是最大值

堆完全二叉树，除了树的最后一层结点不需要是满的，其它的每一层从左到右都是满的，如果最后一层结点不是满的，那么要求左满右不满：

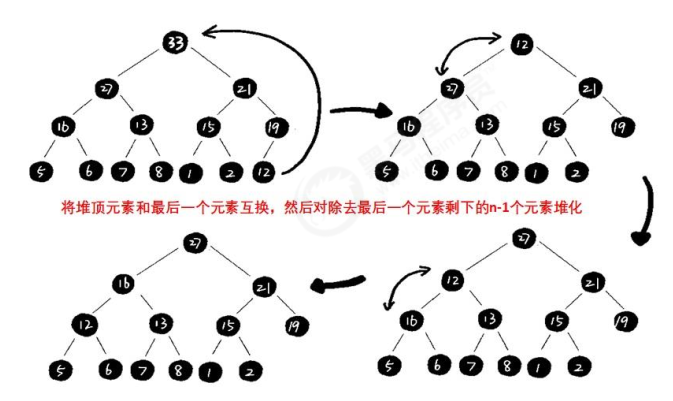
出堆

一个常见的操作是，把根结点和最后一个结点交换。但是新的根结点可能不满足 父节点的权值不小于儿子的权值（大顶堆）。

这个时候，其实只需要将新的根节点下沉到正确位置即可，有如下：

入堆

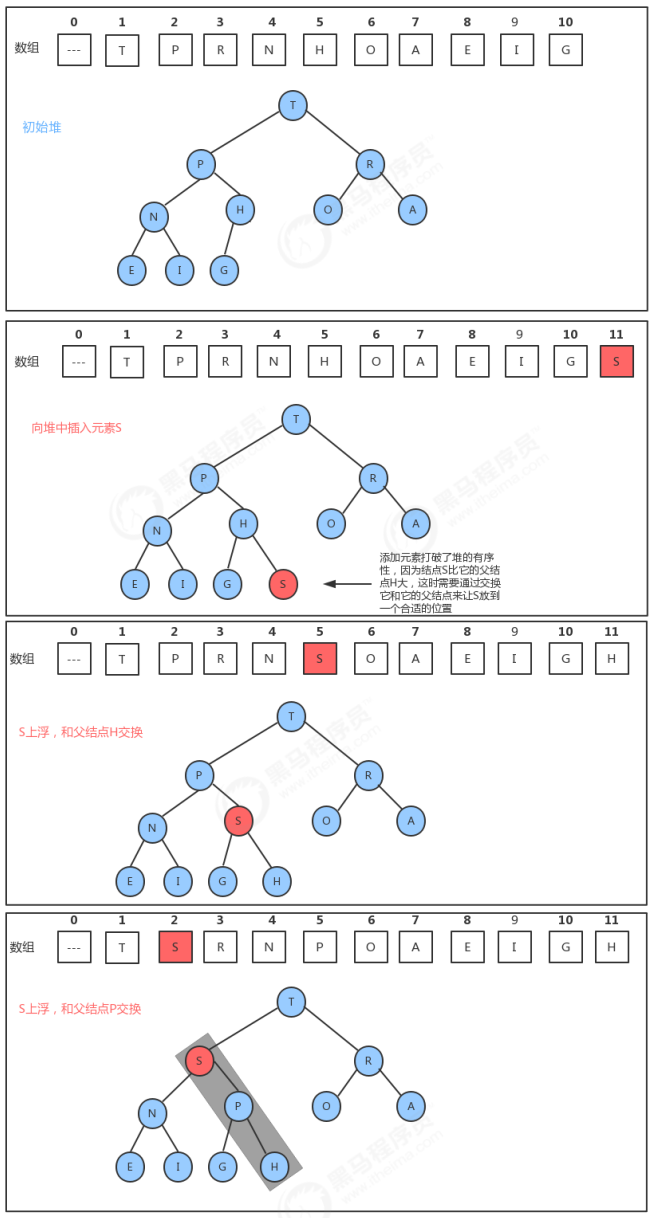
入堆和出堆类似。我们可以直接往树的最后插入一个节点。再进行上浮操作，上浮只需要拿当前节点和父节点进行比对就可以了， 由于省去了判断左右子节点哪个更小的过程，因此更加简单。

下面引用黑马程序员中的一张图：

实现

对于完全二叉树来说使用数组实现非常方便。因为：

• 数组中下标为 k 的节点的左子节点，就是下标为 2k 的节点，右子节点就是下标为2k+1的节点，
• 父节点就是下标为k/2的节点，其中k>=1。
• 另外我们也发现，数组下标为0的位置并未存储数据，这是因为为了方便于在程序中计算，而该位置可以存储堆大小信息

代码实现：

• 小顶堆：父节点的值始终不大于子节点的值

import java.util.Arrays;

public class Heap{

    // 堆
    private int[] datas;
    // 堆中已存储的元素个数
    private int size = 0;

    public Heap(int initialCapacity){
        if (initialCapacity < 1)
            throw new IllegalArgumentException();

        this.datas = new int[initialCapacity + 1];
    }

    public Heap(int[] array){
        this.size = array.length;
        this.datas = new int[array.length + 1];

        int i=1;
        for(int val: array){
            this.datas[i++] = val;
        }
    }

    // 向堆中插入元素
    public void push(int val){
        if(size == this.datas.length-1){
            this.datas = Arrays.copyOf(this.datas, size*2 + 1);
        }
        this.datas[++size] = val;
        swim(size);
    }

    // 堆中取出元素
    public int peek(){
        return this.datas[1];
    }

    // 弹出堆中元素
    public int pop(){
        // 弹出堆顶元素
        int res = this.datas[1];
        // 移除完成后要保证堆的完整性，需要寻找第二大的元素放到堆顶
        // 1.将最后一个元素直接放在堆顶，并减少数据
        this.datas[1] = this.datas[size--];
        // 2.堆化让其继续成为一个合格的堆，此时需要自上而下堆化
        sink(1);

        return res;
    }

    // 建堆
    public void buildHeap(){
        // 对堆中的元素做下沉调整(从长度的一半处开始，往索引1处扫描)
        for (int i = (this.datas.length)/2; i > 0; i--) {
            sink(i);
        }
    }

    // 上浮操作
    private void swim(int end){
        int i = end;
        while( i/2 >0 && this.datas[i/2] > this.datas[i]){
            // 有父节点，且父节点的值大于该节点，则交换
            swap(i, i/2);
            i /= 2;
        }
    }

    // 下沉操作
    private void sink(int start){

        // 通过循环不断的对比当前k结点和其左子结点2*k以及右子结点2k+1处中的较大值的元素大小，
        // 如果当前结点大，则需要交换位置
        while (2*start <= size){

            int min;
            if(2*start+1 <= size){
                // 有右节点的情况
                if(this.datas[2*start] < this.datas[2*start+1]){
                    // 左节点更小
                    min = 2*start;
                }else{
                    // 右节点更小
                    min = 2*start+1;
                }
            }else{
                // 无右节点的情况
                min = 2*start;
            }

            // 与当前节点比较判断是否需要交换
            if(this.datas[start] < this.datas[min]){
                break;
            }
            // 需要交换
            swap(start, min);
            start = min;
        }
    }

    private void swap(int i, int j){
        int tmp = this.datas[i];
        this.datas[i] = this.datas[j];
        this.datas[j] = tmp;
    }

    public static void main(String[] args) {

        int arr[] = new int[]{2,7,4,1,8,1};
        Heap heap = new Heap(arr);
        heap.buildHeap();
        System.out.println(heap.peek());
        heap.push(5);
        heap.push(10);
        heap.push(3);
        while (heap.size > 0) {
            int num = heap.pop();
            System.out.printf(num + "");
        }
    }
}

• 大顶堆：父节点的值始终不小于子节点的值

import java.util.Arrays;

public class Heap{

    // 堆
    private int[] datas;
    // 堆中已存储的元素个数
    private int size = 0;

    public Heap(int initialCapacity){
        if (initialCapacity < 1)
            throw new IllegalArgumentException();

        this.datas = new int[initialCapacity + 1];
    }

    public Heap(int[] array){
        this.size = array.length;
        this.datas = new int[array.length + 1];

        int i=1;
        for(int val: array){
            this.datas[i++] = val;
        }
    }

    // 向堆中插入元素
    public void push(int val){
        if(size == this.datas.length-1){
            this.datas = Arrays.copyOf(this.datas, size*2 + 1);
        }
        this.datas[++size] = val;
        swim(size);
    }

    // 堆中取出元素
    public int peek(){
        return this.datas[1];
    }

    // 弹出堆中元素
    public int pop(){
        // 弹出堆顶元素
        int res = this.datas[1];
        // 移除完成后要保证堆的完整性，需要寻找第二大的元素放到堆顶
        // 1.将最后一个元素直接放在堆顶，并减少数据
        this.datas[1] = this.datas[size--];
        // 2.堆化让其继续成为一个合格的堆，此时需要自上而下堆化
        sink(1);

        return res;
    }

    // 建堆
    public void buildHeap(){
        // 对堆中的元素做下沉调整(从长度的一半处开始，往索引1处扫描)
        for (int i = (this.datas.length)/2; i > 0; i--) {
            sink(i);
        }
    }

    // 上浮操作
    private void swim(int end){
        int i = end;
        while( i/2 >0 && this.datas[i/2] < this.datas[i]){
            // 有父节点，且父节点的值小于该节点，则交换
            swap(i, i/2);
            i /= 2;
        }
    }

    // 下沉操作
    private void sink(int start){

        // 通过循环不断的对比当前k结点和其左子结点2*k以及右子结点2k+1处中的较大值的元素大小，
        // 如果当前结点小，则需要交换位置
        while (2*start <= size){

            int max;
            if(2*start+1 <= size){
                // 有右节点的情况
                if(this.datas[2*start] > this.datas[2*start+1]){
                    // 左节点更大
                    max = 2*start;
                }else{
                    // 右节点更大
                    max = 2*start+1;
                }
            }else{
                // 无右节点的情况
                max = 2*start;
            }

            // 与当前节点比较判断是否需要交换
            if(this.datas[start] > this.datas[max]){
                break;
            }
            // 需要交换
            swap(start, max);
            start = max;
        }
    }

    private void swap(int i, int j){
        int tmp = this.datas[i];
        this.datas[i] = this.datas[j];
        this.datas[j] = tmp;
    }

    public static void main(String[] args) {

        int arr[] = new int[]{2,7,4,1,8,1};
        Heap heap = new Heap(arr);
        heap.buildHeap();
        System.out.println(heap.peek());
        heap.push(5);
        heap.push(10);
        heap.push(3);
        while (heap.size > 0) {
            int num = heap.pop();
            System.out.printf(num + "");
        }
    }
}

三个技巧

技巧1：固定堆

代码上可通过每 pop 出去一个就 push 进来一个来实现。

而由于初始堆可能是 0，我们刚开始需要一个一个 push 进堆以达到堆的大小为 k，因此严格来说应该是维持堆的大小不大于 k。

求第k小的数：

1. 方法1：将所有的数入堆，然后逐个出堆，一同出堆k次，最后一次出堆的就是第k小的数
2. 方法2：建立大顶堆，维持堆的大小为k个。如果新的数入堆之后堆的大小大于 k，则需要将堆顶的数和新的数进行比较，并将较大的移除。这样可以保证堆中的数是全体数字中最小的 k 个，而此时堆顶元素即为第k小的数

总结：

1. 固定一个大小为 k 的大顶堆可以快速求第 k 小的数

   即堆中有k个数，而大顶堆时堆顶的数最大，大于k-1个数，即为第k小的数

2. 固定一个大小为 k 的小顶堆可以快速求第 k 大的数

   即堆中有个k个数，而小顶堆时堆顶的数最小，堆中的k-1个数都比堆顶的数大，即为第k大的数

3. 通过后续两题好好理解上述表述：

   • 295. 数据流的中位数

   • 857. 雇佣 K 名工人的最低成本

技巧2：多路归并

解释：

• 多路体现在：有多条候选路线。代码上，我们可使用多指针来表示。
• 归并体现在：结果可能是多个候选路线中最长的或者最短，也可能是第 k 个等。因此我们需要对多条路线的结果进行比较，并根据题目描述舍弃或者选取某一个或多个路线。

题目（都是hard的题目，需要多理解理解）：

• 1439. 有序矩阵中的第 k 个最小数组和

• 719. 找出第 k 小的距离对

• 632. 最小区间

• 1675. 数组的最小偏移量

  待做

技巧3：事后小诸葛

当从左到右遍历的时候，我们是不知道右边是什么的，需要等到你到了右边之后才知道

如果想知道右边是什么，一种简单的方式是遍历两次，第一次遍历将数据记录下来，当第二次遍历的时候，用上次遍历记录的数据

也可以在遍历到指定元素后，往前回溯，这样就可以边遍历边存储，使用一次遍历即可

• 871. 最低加油次数
• 1488. 避免洪水泛滥
• 1642. 可以到达的最远建筑

四大应用

topK

其实就是固定堆：

1. 固定一个大小为 k 的大顶堆可以快速求第 k 小的数
2. 固定一个大小为 k 的小顶堆可以快速求第 k 大的数

题目：

• 面试题 17.14. 最小K个数
• 692. 前K个高频单词
• 973. 最接近原点的 K 个点

带权最短距离

使用优先队列的 BFS 实现典型的就是 dijkstra 算法。dijkstra 算法主要解决的是图中任意两点的最短距离。

算法的基本思想是贪心，每次都遍历所有邻居，并从中找到距离最小的，本质上是一种广度优先遍历。

// 伪代码
// 定义邻接表
// 邻接表，key:源节点，value:源节点连接的目标节点，其中的int[]中存储了点和权值
Map<Integer, List<int[]>> graph = new HashMap<>();

for(int[] t: times){
 // 构建邻接表
 if(!graph.containsKey(t[0])){
     // 这个源节点还没有加入邻接表，则加入
     graph.put(t[0], new ArrayList<>());
 }
 // 放入目标点和权值
 graph.get(t[0]).add(new int[]{t[1], t[2]});
}

// dijkstra，输入：邻接表，节点数，开始节点，结束节点
public int dijkstra(Map<Integer, List<int[]>> graph, int N, int start, int end){

 // 如果走完所有点，那么不会有 Integer.MAX_VALUE，否则就是没走完
 int[] dis = new int[N + 1];
 Arrays.fill(dis, Integer.MAX_VALUE);
 // 标记节点是否已经被访问过
 boolean[] visited = new boolean[N + 1];

 // 将起点和冗余点的距离设为0
 dis[start] = 0;
 dis[0] = 0; // 这里节点是从1开始标号的

 // 建立优先队列，长度大的会自动排到后面
 Queue<Integer> queue = new PriorityQueue<>((o1, o2) -> dis[o1] - dis[o2]);
 queue.offer(start);

 while (!queue.isEmpty()) {
     int node = queue.poll();
     // 该节点是否访问过
     if (visited[node]) continue;
     visited[node] = true;

     if(node == end){
 		// 后面开始访问这个节点的相邻节点了，没必要了，可以直接返回了
         return dis[node];
     }

     // 邻接表中有这个key时，就弹出相邻节点，否则弹出空的
     List<int[]> list = graph.getOrDefault(node, Collections.emptyList());
     for (int[] arr : list) {  // 遍历相邻节点
         int next = arr[0];
         if (visited[next]) continue;
         // 如果长度较长，那么会自动移到后面
         // 贪心思想。如果d[1] > d[2]，那么不可能会有0 -> 2 -> 1的距离大于0 -> 1的距离
         // 所以可以直接在满足条件的基础上入队
         dis[next] = Math.min(dis[next], dis[node] + arr[1]);
         queue.offer(next);
     }
 }
 return -1;
}

好好体会下面两题：

• 743. 网络延迟时间

• 787. K 站中转内最便宜的航班

因子分解

263. 丑数、264. 丑数 II、313. 超级丑数

堆排序

int[] array = {1,2,3,4,5};
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b)->b - a);

for (int i = 0; i < array.length; i++) {
    maxHeap.offer(array[i]);
}

while (!maxHeap.isEmpty()){
    System.out.println(maxHeap.poll());
}

这里用了库函数，也可用上方基于数据实现的二叉堆进行替换

题目

典型题目

索引

• 1046. 最后一块石头的重量
• 263. 丑数
• 264. 丑数 II
• 313. 超级丑数
• 1206. 设计跳表【待做】
• 295. 数据流的中位数
• 857. 雇佣 K 名工人的最低成本
• 1439. 有序矩阵中的第 k 个最小数组和
• 719. 找出第 k 小的距离对
• 632. 最小区间
• 1675. 数组的最小偏移量【待做】
• 871. 最低加油次数
• 1488. 避免洪水泛滥
• 1642. 可以到达的最远建筑
• 面试题 17.14. 最小K个数
• 692. 前K个高频单词
• 973. 最接近原点的 K 个点
• 743. 网络延迟时间
• 787. K 站中转内最便宜的航班

题目

1046. 最后一块石头的重量

public int lastStoneWeight(int[] stones) {

    int length = stones.length;
    // 直接上优先队列
    PriorityQueue<Integer> maxHeap = new PriorityQueue<>(length, (a, b) -> b-a);

    for(int stone: stones){
        maxHeap.offer(stone);
    }

    while(maxHeap.size() >= 2){
        Integer s1 = maxHeap.poll();
        Integer s2 = maxHeap.poll();

        if(s1.equals(s2)){
            // 都碎了
            continue;
        }
        maxHeap.offer(s1 - s2);
    }

    if(maxHeap.size() == 0){
        return 0;
    }else{
        return maxHeap.poll();
    }

}

263. 丑数

public boolean isUgly(int num) {

    if( num <= 0){
        return false;
    }

    while(num % 5 == 0){
        num /= 5;
    }

    while(num % 3 == 0){
        num /= 3;
    }

    while(num % 2 == 0){
        num /= 2;
    }

    if(num == 1){
        return true;
    }else{
        return false;
    }
}

264. 丑数 II

// // 方法1：三指针法
public int nthUglyNumber(int n) {

    int[] reuslt = new int[n];

    reuslt[0] = 1;

    // 定义三个指针
    int p1=0, p2=0, p3=0;
    for(int i=1; i<n; i++){

        reuslt[i] = Math.min(reuslt[p1]*2, Math.min(reuslt[p2]*3, reuslt[p3]*5));

        System.out.println(reuslt[i]);

        if(reuslt[i] == reuslt[p1]*2) p1++;
        if(reuslt[i] == reuslt[p2]*3) p2++;
        if(reuslt[i] == reuslt[p3]*5) p3++;
    }

    return reuslt[n-1];
}

// 方法2：堆，每次都往堆里添加如下： [2 3 5] * 堆中的最小值
public int nthUglyNumber(int n){

    // int 会爆的
    PriorityQueue<Long> minHeap = new PriorityQueue<>();
    int count = 0;

    long ans = 1;  // 第一个元素
    minHeap.offer(ans);

    while(count < n){

        ans = minHeap.poll();
        // System.out.println(ans);

        // 堆中的数据不是严格递增的，会存在重复数据
        while(!minHeap.isEmpty() && ans==minHeap.peek()){
            minHeap.poll();
        }

        count++;

        // 往堆里添加内容
        minHeap.offer(ans*2);
        minHeap.offer(ans*3);
        minHeap.offer(ans*5);
    }
    return (int)ans;
}

313. 超级丑数

// 方法1：多指针法
public int nthSuperUglyNumber(int n, int[] primes) {

    int[] result = new int[n];
    result[0] = 1;

    // 多指针定义
    int[] index = new int[primes.length];

    for(int i=1; i<n; i++){

        int min = Integer.MAX_VALUE;
        for(int j=0; j<primes.length; j++){
            int tmp = result[index[j]] * primes[j];
            min = Math.min(min, tmp);
        }

        result[i] = min;

        for(int j=0; j<primes.length; j++){
            if(result[i] == result[index[j]]*primes[j]) index[j] ++;
        }
    }
    return result[n-1];
}

// 方法2：堆
public int nthSuperUglyNumber(int n, int[] primes) {
    // int 会爆的
    PriorityQueue<Long> minHeap = new PriorityQueue<>();
    int count = 0;

    long ans = 1;  // 第一个元素
    minHeap.offer(ans);

    while(count < n){

        ans = minHeap.poll();

        // 堆中的数据不是严格递增的，会存在重复数据
        while(!minHeap.isEmpty() && ans==minHeap.peek()){
            minHeap.poll();
        }

        count++;

        // 往堆里添加内容
        for(int i=0; i<primes.length; i++){
            minHeap.offer(primes[i]*ans);
        }
    }
    return (int)ans;
}

295. 数据流的中位数

class MedianFinder {

    private Queue<Integer> minHeap, maxHeap;
    /** initialize your data structure here. */
    public MedianFinder() {
        // 建立两个堆，一个大顶堆，一个小顶堆
        // 大顶堆中放入 (n+1)/2 个元素，即存储了一半的小值
        // 小顶堆中放入, 存储了一半的大值
        minHeap = new PriorityQueue<>();
        maxHeap = new PriorityQueue<>((a, b) -> b-a);
    }

    public void addNum(int num) {
        // 两个堆之间的元素是需要平衡的
        maxHeap.offer(num); // 保证了最大堆中的数始终大于等于最小堆的值，在奇数时，其堆顶就为中位数
        minHeap.offer(maxHeap.poll());  // 在偶数时，堆顶加大顶堆的堆顶/2就是中位数
        if(maxHeap.size() < minHeap.size()){
            maxHeap.offer(minHeap.poll());
        }
    }

    public double findMedian() {
        if(minHeap.size() == maxHeap.size()){
            return (maxHeap.peek() + minHeap.peek()) / 2.0;
        }else{
            return maxHeap.peek();
        }
    }
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */

857. 雇佣 K 名工人的最低成本

public double mincostToHireWorkers(int[] quality, int[] wage, int K) {
    int n = quality.length;

    // key:性价比：工作质量/最低工资   value:工作质量
    Pair<Double, Integer>[] pairs = new Pair[n];
    for(int i=0; i<n; i++){
        Pair<Double, Integer> pair = new Pair(quality[i] / (wage[i]*1.0), quality[i]);
        pairs[i] = pair;
    }

    // 按照性价比降序排序, 有A的性价比低于B的性价比，则按照B发工资时，A是达不到最低工资的
    Arrays.sort(pairs, (o1, o2) -> o2.getKey() - o1.getKey() > 0 ? 1 : -1);

    // 最终总工资
    double ans = Double.MAX_VALUE;
    // 总工作质量
    int sumQuality = 0;
    // 对工作质量进行堆排序，最大堆
    PriorityQueue<Integer> queue = new PriorityQueue<>((a,b)->b-a);
    for(int i=0; i<n; i++){
        // 按照性价比从高到低开始弹出工人，后面性价比低的工人可以满足前面性价比高的工人的最低工资，反之不然
        Pair<Double, Integer> pair = pairs[i];
        queue.offer(pair.getValue());
        sumQuality += pair.getValue();

        if(queue.size() > K){
            // 堆里的人已经超过K了，则弹出最大工作质量的人，因为每次计算的时候性价比都是一定的
            // 且是按照性价比最低的人的标准进行计算的
            sumQuality -= queue.poll();
        }
        if(queue.size() == K){
            // 人已经齐了，这时候就要计算 总工资了
            ans = Math.min(ans, sumQuality / pair.getKey());
        }
    }

    return ans;
}

1439. 有序矩阵中的第 k 个最小数组和

// 方法1：使用最小堆，出堆k次就是所求值
public int kthSmallest(int[][] mat, int k) {
    // 行数：指针数
    int m = mat.length;
    // 列数
    int n = mat[0].length;

    // 最小堆:Pait: key-值，Value-指针信息
    PriorityQueue<Pair<Integer, int[]>> pq = new PriorityQueue<>((a,b) -> a.getKey() - b.getKey());
    // 指针信息
    int[] points = new int[m];
    int total = 0;
    for(int i=0; i<m; i++){
        // 最开始的最小值，就是矩阵每行的首个元素和
        total += mat[i][0];
    }
    // 堆中的第一个元素是确定的
    Pair<Integer, int[]> pair = new Pair<>(total, points);
    pq.offer(pair);

    // 记录指针的情况是否出现过，顺序问题
    // 两个数组，先移动1，在移动2，和先移动2，再移动1，会出现重复的情况
    Set<String> visited = new HashSet<>();

    // 小顶堆 执行k次 把前面k小的数组移除 之后栈顶便是我们所求之结果
    while(--k > 0){  // 第一个元素已经添加进堆了
        Pair<Integer, int[]> cur = pq.poll();

        // 遍历每一行
        for(int i=0; i<m; i++){
            // 第i行还有元素可以遍历
            if(cur.getValue()[i] < n-1){
                // 当前的指针情况
                int[] arr = Arrays.copyOf(cur.getValue(), m);
                // 列号，即该行向后遍历一个元素
                arr[i]++;
                // 这种组合还没出现过, eg:[1,1]是否出现过
                if(!visited.contains(Arrays.toString(arr))){
                    visited.add(Arrays.toString(arr));
                    // 一种新的情况，需要先减去改行上一个值然后加上新指向的值
                    int next = cur.getKey() - mat[i][cur.getValue()[i]] + mat[i][arr[i]];
                    pq.offer(new Pair<>(next, arr));
                }
            }
        }
    }
    return pq.peek().getKey();
}

// 方法2：暴力法，按行遍历数组，同时把改行的数据都加起来，遍历完所有行时，即算完了所有可能
public int kthSmallest(int[][] mat, int k) {
    int m = mat.length;
    int n = mat[0].length;
    List<Integer> list = new ArrayList<>();
    list.add(0);
    // 遍历了每一行
    for (int r = 0; r < m; r++) {
        List<Integer> temp = new ArrayList<>();
        // 把该行中的所有列都加到原有的数据上
        for (Integer num : list) {
            for (int c = 0; c < n; c++) {
                int cur = num + mat[r][c];
                temp.add(cur);
            }
        }
        Collections.sort(temp);
        // 删除一些不需要再参与计算的数
        list = temp.subList(0, Math.min(k, temp.size()));
    }
    return list.get(list.size() - 1);
}

719. 找出第 k 小的距离对

// 方法1：固定堆，即维护固定K个元素的大顶堆，则堆顶元素就是第K小的元素
// BUT:超出限制!
public int smallestDistancePair(int[] nums, int k) {

    // 大顶堆, K个元素的固定大顶堆，则堆顶元素即为第k个最小元素
    PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b)-> b - a);

    for(int i=0; i<nums.length; i++){
        for(int j=i+1; j<nums.length; j++){
            int num = Math.abs(nums[i]-nums[j]);

            // 对的尺寸已经为k了，则选择更小的入堆
            if(maxHeap.size() == k && maxHeap.peek() > num){
                maxHeap.poll();
            }

            // 堆还没有到k的大小，进堆
            if(maxHeap.size() < k){
                maxHeap.offer(num);
            }
        }
    }

    return maxHeap.peek();
}

// 方法2：多指针（双）
// BUT:还是超出时间限制了，在最后一个测试案例上
public int smallestDistancePair(int[] nums, int k) {
    // 先对数组进行排序，最小的值肯定首先出现在相邻的元素之间
    Arrays.sort(nums);
    // 建立一个小顶堆，key：值  value：指针信息
    PriorityQueue<Pair<Integer, int[]>> pq = new PriorityQueue<>((a,b) -> a.getKey() - b.getKey()); 

    int[] points = new int[2];
    Pair<Integer, int[]> pair = null;
    // 第一次遍历数组
    for(int i=0; i+1<nums.length; i++){
        points = new int[2];
        points[0] = i;
        points[1] = i+1;
        // 显而易见，当数组排序后，最小的值必然出现在相邻的元素间
        pair = new Pair<>(nums[i+1] - nums[i], points);
        pq.offer(pair);
    }

    while( --k > 0){
        pair = pq.poll();
        points = pair.getValue();
        // 当最小的值出堆后，继续添加新的情况，只需要移动第二个指针往后走一步即可
        if(points[1]+1 < nums.length){
            points[1] ++;
            pair = new Pair<>(nums[points[1]] - nums[points[0]], points);
            pq.offer(pair);
        }
    }

    return pq.peek().getKey();
}

// 方法3：二分法，还没做...等刷二分专题的时候再说吧
public int smallestDistancePair(int[] nums, int k) {
    // ???
}

632. 最小区间

public int[] smallestRange(List<List<Integer>> nums) {

    // 结果的 左范围          右范围            遍历过程中的最大值，最小值是保存到了堆中
    int res_left= -100000, res_right=100000, max=-100000;

    // 建立一个最小堆，存储的是：[rows, cols, val]
    PriorityQueue<int[]> pq = new PriorityQueue((Comparator<int[]>) (a, b) -> a[2] - b[2]);

    // 首先指针都指向第一个元素
    for (int i = 0; i < nums.size(); i++) {
        pq.offer(new int[]{i, 0, nums.get(i).get(0)});
        max = Math.max(max, nums.get(i).get(0));
    }

    while( !pq.isEmpty() ){
        int[] item = pq.poll();
        // 获取堆中最小的值，移动指针，这样数组的差距就会变小
        int minV = item[2], row = item[0], col = item[1];
        // 计算现在的diff
        if(res_right - res_left > max - minV){
            res_right = max;
            res_left = minV;
        }

        // 一旦有一行已经遍历结束，后续再出堆入堆已经没意义了，可以画图理解
        if(col+1 == nums.get(row).size()){
            return new int[]{res_left, res_right};
        }

        // 移动最小值的指针
        int next = nums.get(row).get(col + 1);
        pq.offer(new int[]{row, col + 1, next});
        // 更新最大值
        max = Math.max(next, max);
    }

    return new int[]{res_left, res_right};
}

871. 最低加油次数

public int minRefuelStops(int target, int startFuel, int[][] stations) {
    // 没有加油站的情况
    if (stations.length == 0) {
        return startFuel >= target ? 0 : -1;
    }

    // 定义次数 ans，车内油量 cur
    int ans = 0, cur = startFuel;
    // 定义最大堆,假定每次过加油站都把加油站的油带上
    PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> b - a);

    for(int i=0; i<stations.length; i++){
        while(cur < stations[i][0]){
            // 车上没油啦 需要到车厢找此时车上最大的一桶油来加满
            Integer fuel = pq.poll();
            // 车厢里已经没油了
            if(fuel == null){
                return -1;
            }
            // 加了此时最多的油
            cur += fuel;
            ans++;
        }

        // 若我能到这个加油站，我就假定把油都给带上了
        pq.offer(stations[i][1]);
    }

    // 前面判断的是能否达到所有的加油站，
    // 现在判断是否到达目的地
    while(cur < target){
        // 现在的油是否能达到目的地，不能到的话再取油加上
        Integer fuel = pq.poll();
        if (fuel == null) {
            return -1;
        }
        cur += fuel;
        ans++;
    }
    return ans;
}

1488. 避免洪水泛滥

public int[] avoidFlood(int[] rains) {

    // 定义一个晴天的队列，先进先出
    List<Integer> sunnys = new ArrayList<>();

    // 记录湖的状态 key：湖   value：第几天被填满的
    Map<Integer,Integer> rainings = new HashMap<>();

    int res[] = new int[rains.length];

    for(int i=0; i<rains.length; i++){
        if(rains[i] > 0){
            // rains[i]个湖泊下雨了
            if(rainings.containsKey(rains[i])){
                // 这个湖泊已经满了，即之前下过雨，马上则取之前的一个晴天来抽水
                if(sunnys.size() == 0){
                    // 没有晴天了，抽水失败
                    return new int[0];
                }
                // 有晴天可以用，则选择湖泊被填满之后的最早的一个晴天来抽水
                int sunday = useOneSunday(sunnys, rainings.get(rains[i]));
                res[sunday] = rains[i];
                if(sunday == 0){
                    // sunday为0说的是，没有找到能用晴天
                    return new int[0];
                }
            }

            // 湖泊rains[i]水满了
            rainings.put(rains[i], i);
            // 这天做不了操作
            res[i] = -1;
        }else{
            // 当前湖泊没有下雨,记录晴天
            sunnys.add(i);
        }
    }

    // 多余的没有操作的晴天都给1，和答案一样
    int suns = sunnys.size();
    for(int i=0; i<suns; i++){
        res[sunnys.get(i)] = 1;
    }
    return res;
}

private int useOneSunday(List<Integer> sunnys, int rainday){

    int sunday=0;
    for(int i=0; i<sunnys.size(); i++){
        // 晴天的时间要大于被填满的日期，同时选择最小的
        if(sunnys.get(i) > rainday){
            sunday = sunnys.get(i);
            sunnys.remove(Integer.valueOf(sunday));
            break;
        }
    }
    return sunday;
}

1642. 可以到达的最远建筑

public int furthestBuilding(int[] heights, int bricks, int ladders) {

    // 每次跨楼需要的砖块数量
    int needBrick = 0;
    // 最小堆，存每层建筑之前需要的砖块数量，
    // 起初都无脑梯子，当梯子用完后，发现现在的高度小于之前的高度，则替换之前用砖，这次再用梯子
    PriorityQueue<Integer> pq = new PriorityQueue<>();

    for(int i=1; i<heights.length; i++){
        // 楼层差
        int diff = heights[i] - heights[i-1];

        if(diff > 0){
            // 需要用梯子/砖块
            pq.offer(diff);
            if(pq.size() > ladders){
                // 梯子已经用完了，现在开始替换
                int brick = pq.poll();
                needBrick += brick;
            }

            if(needBrick > bricks){
                // 梯子没了/砖也没了
                return i-1;  // 返回下标
            }
        }
    }

    return heights.length - 1;
}

面试题 17.14. 最小K个数

public int[] smallestK(int[] arr, int k) {

    int[] res = new int[k];

    if(k==0){
        return res;
    }

    // 建立一个大顶堆，大小固定为k
    PriorityQueue<Integer> pq = new PriorityQueue<>((a,b) -> b-a);

    for(int i=0; i<arr.length; i++){

        if(pq.size() < k){
            pq.offer(arr[i]);
        }else{
            int max = pq.peek();
            if(max > arr[i]){
                pq.poll();
                pq.offer(arr[i]);
            }
        }
    }

    for(int i=0; i<k; i++){
        res[i] = pq.poll();
    }

    return res;
}

692. 前K个高频单词

public List<String> topKFrequent(String[] words, int k) {

    List<String> res = new ArrayList<>();

    // 建立一个 Map 进行保存 key：字符串  value：出现次数
    Map<String, Integer> map = new HashMap<>();

    // 建立一个大顶堆，并给定比较规则
    PriorityQueue<Pair<Integer, String>> maxHeap = new PriorityQueue<>((o1, o2) -> {
        if(o2.getKey()>o1.getKey()){
            return 1;
        }else if(o2.getKey()<o1.getKey()){
            return -1;
        }else {
            return o1.getValue().compareTo(o2.getValue());  // 当频率相同时，按字母顺序排序
        }
    });

    // key：出现次数   value：对应的字符串
    Pair<Integer, String> pair = null;

    // 先遍历一遍，记录下每个字符出现的次数
    for(int i=0; i<words.length; i++){
        if(map.containsKey(words[i])){
            int val = map.get(words[i]);
            val++;
            map.put(words[i], val);
        }else{
            map.put(words[i], 1);
        }
    }

    // 遍历map，放入堆中，进行堆排序
    for (String word: map.keySet()){
        pair = new Pair(map.get(word), word);
        maxHeap.offer(pair);
    }

    for(int i=0; i<k; i++){
        pair = maxHeap.poll();
        res.add(pair.getValue());
    }

    return res;
}

973. 最接近原点的 K 个点

public int[][] kClosest(int[][] points, int K) {

    int[][] res = new int[K][2];
    // 维持一个大顶堆，长度为K，保存的是最小的k个元素，即结果
    PriorityQueue<Pair<Integer, int[]>> maxHeap =
        new PriorityQueue<>((a,b) -> b.getKey()-a.getKey());

    // key:距离  value;对应的点
    Pair<Integer, int[]> pair = null;

    for(int i=0; i<points.length; i++){
        int[] point = new int[2];
        // 距离计算
        int val = points[i][0]*points[i][0] + points[i][1]*points[i][1];
        point[0] = points[i][0];
        point[1] = points[i][1];

        // 当堆的尺寸小于k时，直接入堆，大于时则选择比堆顶小的元素入堆
        if(maxHeap.size() < K){
            pair = new Pair(val, point);
            maxHeap.offer(pair);
        }else{
            pair = maxHeap.peek();
            if(pair.getKey() > val){
                maxHeap.poll();
                maxHeap.offer(new Pair(val, point));
            }
        }
    }

    // 从大到小保存结果
    for(int i=K-1; i>=0; i--){
        pair = maxHeap.poll();
        res[i] = pair.getValue();
    }

    return res;
}

743. 网络延迟时间

结合：787. K 站中转内最便宜的航班理解

public int networkDelayTime(int[][] times, int N, int K) {

    // 邻接表，key:源节点，value:源节点连接的目标节点，其中的int[]中存储了点和权值
    Map<Integer, List<int[]>> graph = new HashMap<>();

    for(int[] t: times){
        // 构建邻接表
        if(!graph.containsKey(t[0])){
            // 这个源节点还没有加入邻接表，则加入
            graph.put(t[0], new ArrayList<>());
        }
        // 放入目标点和权值
        graph.get(t[0]).add(new int[]{t[1], t[2]});
    }

    int max = -1;
    for (int i=1; i<=N; i++){

        int dis = dijkstra(graph, N, K, i);
        if(dis == -1){
            return -1;
        }
        max = Math.max(dis, max);
    }

    return max;
}

public int dijkstra(Map<Integer, List<int[]>> graph, int N, int start, int end){

    // 如果走完所有点，那么不会有 Integer.MAX_VALUE，否则就是没走完
    int[] dis = new int[N + 1];
    Arrays.fill(dis, Integer.MAX_VALUE);
    // 标记节点是否已经被访问过
    boolean[] visited = new boolean[N + 1];

    // 将起点和冗余点的距离设为0
    dis[start] = 0;
    dis[0] = 0; // 这里节点是从1开始标号的

    // 建立优先队列，长度大的会自动排到后面
    Queue<Integer> queue = new PriorityQueue<>((o1, o2) -> dis[o1] - dis[o2]);
    queue.offer(start);

    while (!queue.isEmpty()) {
        int node = queue.poll();
        // 该节点是否访问过
        if (visited[node]) continue;
        visited[node] = true;

        if(node == end){
            return dis[node];
        }

        // 邻接表中有这个key时，就弹出相邻节点，否则弹出空的
        List<int[]> list = graph.getOrDefault(node, Collections.emptyList());
        for (int[] arr : list) {  // 遍历相邻节点
            int next = arr[0];
            if (visited[next]) continue;
            // 如果长度较长，那么会自动移到后面
            // 贪心思想。如果d[1] > d[2]，那么不可能会有0 -> 2 -> 1的距离大于0 -> 1的距离
            // 所以可以直接在满足条件的基础上入队
            dis[next] = Math.min(dis[next], dis[node] + arr[1]);
            queue.offer(next);
        }
    }
    return -1;
}

// 对上述方法的优化：
// 迪杰斯特拉算法的典例
public int networkDelayTime(int[][] times, int N, int K) {
    // 邻接表，key:源节点，value:源节点连接的目标节点，其中的int[]中存储了点和权值
    Map<Integer, List<int[]>> map = new HashMap<>();
    // 如果走完所有点，那么不会有 Integer.MAX_VALUE，否则就是没走完
    int[] dis = new int[N + 1];
    Arrays.fill(dis, Integer.MAX_VALUE);
    // 标记节点是否已经被访问过
    boolean[] visited = new boolean[N + 1];

    for(int[] t: times){
        // 构建邻接表
        if(!map.containsKey(t[0])){
            // 这个源节点还没有加入邻接表，则加入
            map.put(t[0], new ArrayList<>());
        }
        // 放入目标点和权值
        map.get(t[0]).add(new int[]{t[1], t[2]});
    }

    // 将起点和冗余点的距离设为0
    dis[K] = 0;
    dis[0] = 0; // 这里节点是从1开始标号的
    // 建立优先队列，长度大的会自动排到后面
    Queue<Integer> queue = new PriorityQueue<>((o1, o2) -> dis[o1] - dis[o2]);
    queue.offer(K);

    while (!queue.isEmpty()) {
        int node = queue.poll();
        // 该节点是否访问过
        if (visited[node]) continue;
        visited[node] = true;
        // 邻接表中有这个key时，就弹出相邻节点，否则弹出空的
        List<int[]> list = map.getOrDefault(node, Collections.emptyList());
        for (int[] arr : list) {  // 遍历相邻节点
            int next = arr[0];
            if (visited[next]) continue;
            // 如果长度较长，那么会自动移到后面
            // 贪心思想。如果d[1] > d[2]，那么不可能会有0 -> 2 -> 1的距离大于0 -> 1的距离
            // 所以可以直接在满足条件的基础上入队
            dis[next] = Math.min(dis[next], dis[node] + arr[1]);
            queue.offer(next);
        }
    }
    Arrays.sort(dis);
    int max = dis[dis.length - 1];
    return max == Integer.MAX_VALUE ? -1 : max;
}

787. K 站中转内最便宜的航班

结合：743. 网络延迟时间理解

public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) {

    // 邻接表，key:源节点，value:源节点连接的目标节点，其中的int[]中存储了点和权值
    Map<Integer, List<int[]>> map = new HashMap<>();
    // 标记节点是否已经被访问过,第一个为节点，第二个为层
    boolean[][] visited = new boolean[n][K+2];

    for(int[] f: flights){
        // 构建邻接表
        if(!map.containsKey(f[0])){
            // 这个源节点还没有加入邻接表，则加入
            map.put(f[0], new ArrayList<>());
        }
        // 放入目标点和权值
        map.get(f[0]).add(new int[]{f[1], f[2]});
    }

    // 这里由于中转次数不能大于k次，因此建立数组[3] 1:花费  2:节点 3:第几次转
    // 建立优先队列，长度大的会自动排到后面
    Queue<int[]> queue = new PriorityQueue<>((o1, o2) -> o1[0] - o2[0]);
    queue.offer(new int[]{0, src, 0});

    while (!queue.isEmpty()) {
        int[] res = queue.poll();
        // 当前的节点
        int node = res[1];
        // 表示当前是低几次中转
        int layer = res[2];
        // 该节点是否访问过
        if (visited[node][layer]) continue;
        visited[node][layer] = true;

        // 不同之处
        if(node == dst){
            // 到目的地了
            return res[0];
        }else if(layer > K){
            // 中转次数到了  无法再中转了
            continue;
        }

        // 邻接表中有这个key时，就弹出相邻节点，否则弹出空的
        List<int[]> list = map.getOrDefault(node, Collections.emptyList());
        for (int[] arr : list) {  // 遍历相邻节点
            int next = arr[0];
            if (visited[next][layer]) continue;

            int[] temp = new int[3];
            temp[0] = res[0] + arr[1];
            temp[1] = next;
            temp[2] = layer+1;
            queue.offer(temp);
        }
    }
    return -1;
}

其他题目

索引

[狗头]还没做

题目

无