对于multitaper多窗口谱估计的理解及步骤 (对应matlab中pmtm函数）谱减法相关

对于多窗口谱估计的理解

目录

• 对于多窗口谱估计的理解
  • 0. 缘起
  • 1. PMTM 含义
  • 2. 与我们常用的周期谱估计的区别
  • 3. 计算过程
  • 5. 多窗/单窗谱估计结果对比
  • 6. 程序如何生成多窗 - 以sin为例
    • 6.1 生成正交窗的公式代码
    • 6.2 计算是否符合正交
  • 7. Reference

0. 缘起

在语音增强通过改进的谱减法进行谱估计时，使用多窗谱估计法要优于我们一般遇到的周期法谱估计，中文相关的资料不多，这里分享一下我学习理解到的内容。

1. PMTM 含义

• P: PSD (Power spectral density)
• MTM: Multi- Taper Method

2. 与我们常用的周期谱估计的区别

• 正常的周期法: 频率估计是取帧，一帧加窗(一般汉宁窗)然后做频率变换,然后将每帧的频谱做一个平均
• 多窗谱法：频率估计是取帧，一帧分别与多窗(一般为几个k不一样的slepian窗)中的每个窗相乘，然后做频率变换, 将每个窗频率变换的结果 相加得到最终的一帧频谱结果

PMTM 中常用的窗函数：

• Slepian

• Sine

  

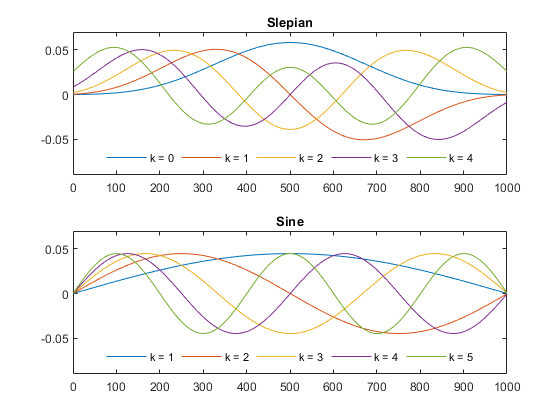
  k不同，窗口不同，他们是正交的。即 向量积为0.

3. 计算过程

• step 1: 取一帧数据，分别与窗相乘，得多几条加窗后的数据
  
  

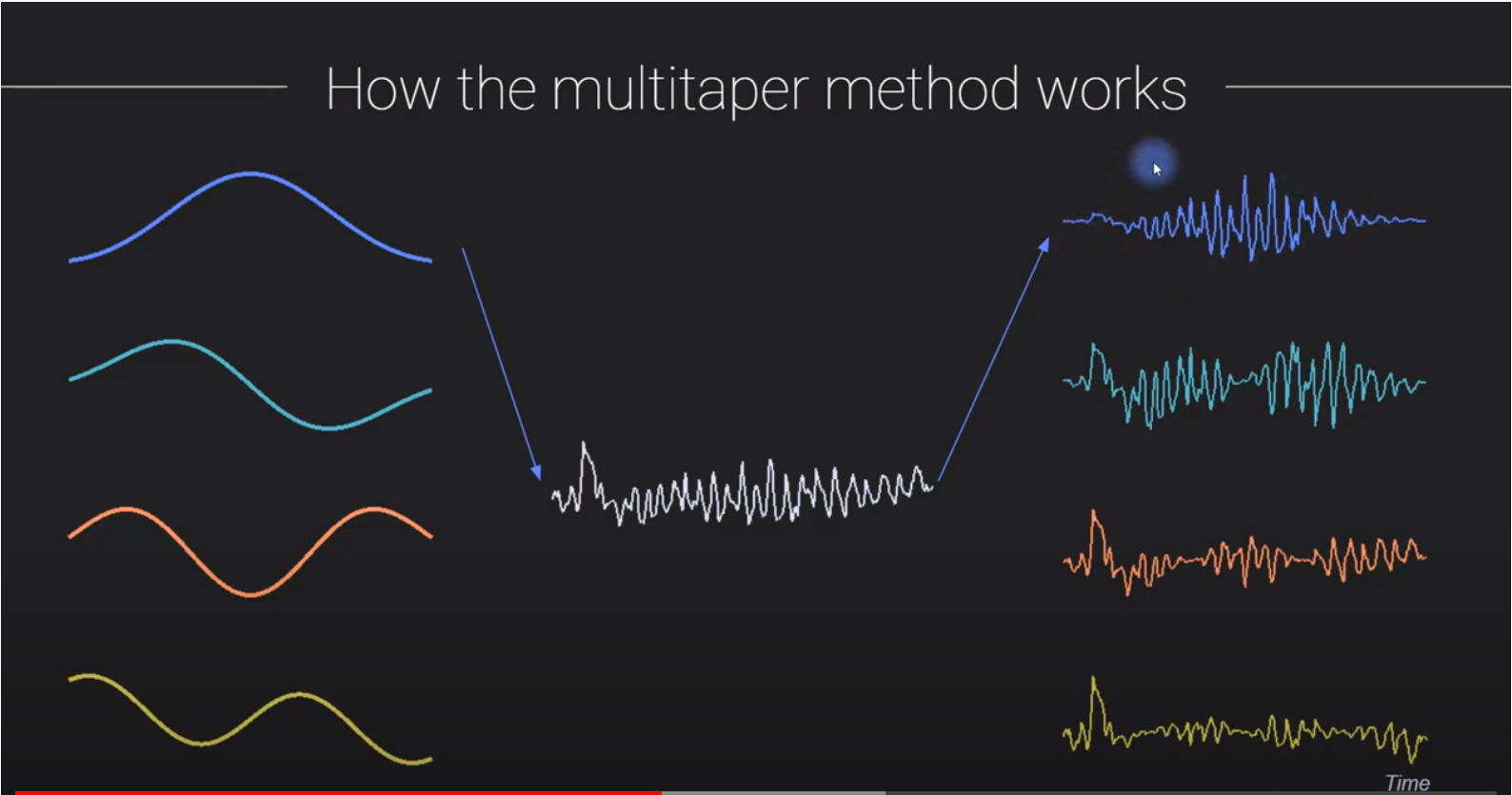
• step2: 针对每条数据（同一帧，不同加窗），进行 FFT变换

  
  
  

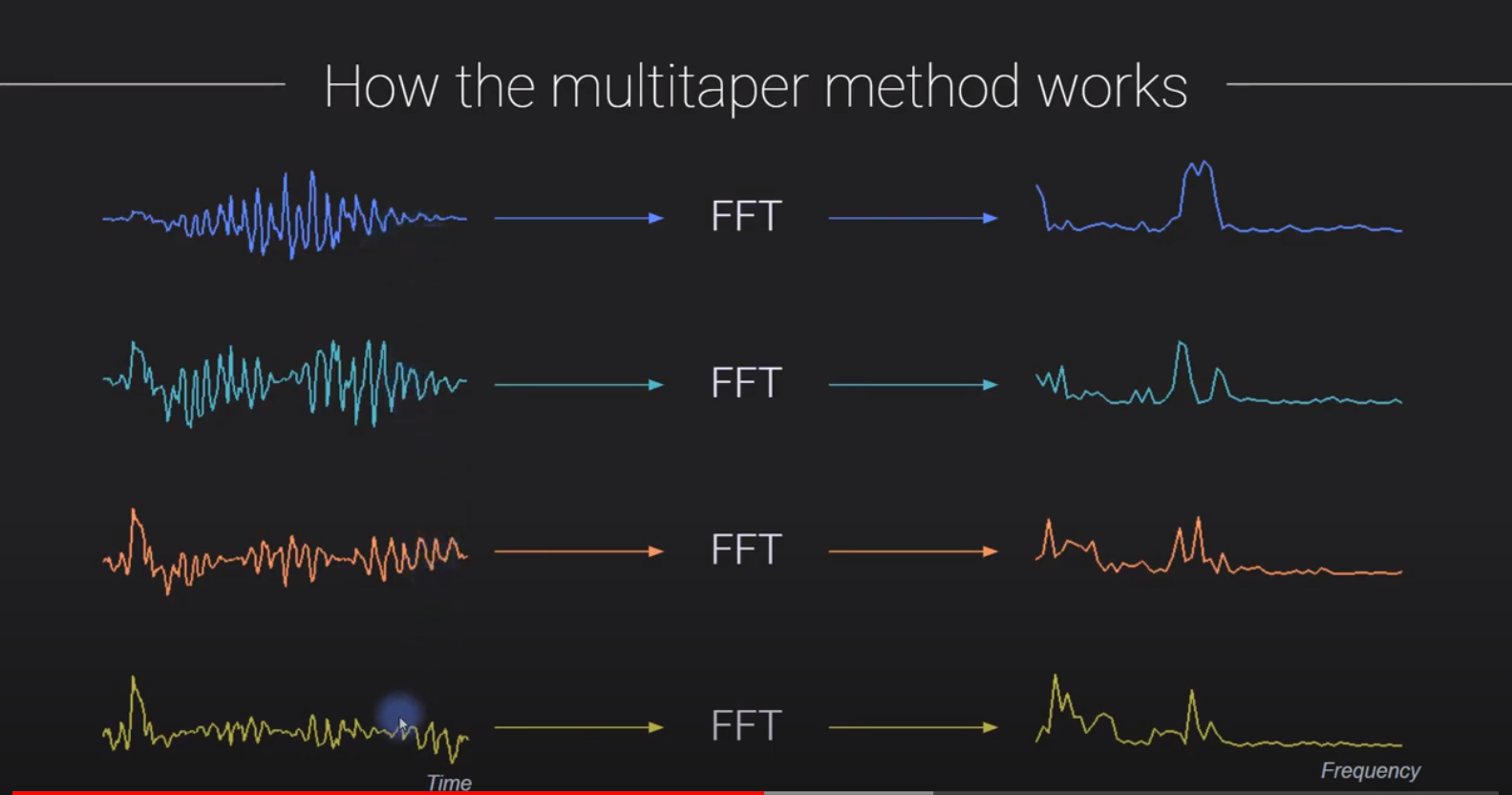
• step3: 将这几条数据（同一帧，不同加窗）的FFT结果相加后平均，得多合成的一帧频谱变换

  

• overview

  

5. 多窗/单窗谱估计结果对比

• 多窗谱估计得到的结果没有一般的周期法用的单窗谱估计得到的结果那么锐利

  

6. 程序如何生成多窗 - 以sin为例

6.1 生成正交窗的公式代码

\[g_k{(n)}=\sqrt{\frac{2}{N+1}}sin(\frac{\pi nk}{N+1}) \qquad n,k=1,2,...N.
\]

N为数据的点数

figure
N = 1000;
nw = 3;
ns = 2*(nw)-1;

n = 1:N;
k = 1:ns;

sine_tprs_array = sqrt(2/(N+1))*sin(pi*n'*k/(N+1));   % 生成多窗口函数
% g_1(n)= sqrt(2/(1000+1))*sin(pi*(1:1000)'*1/(1000+1))
% g_2(n)= sqrt(2/(1000+1))*sin(pi*(1:1000)'*2/(1000+1))
% g_3(n)= sqrt(2/(1000+1))*sin(pi*(1:1000)'*3/(1000+1))
% g_4(n)= sqrt(2/(1000+1))*sin(pi*(1:1000)'*3/(1000+1))
% g_5(n)= sqrt(2/(1000+1))*sin(pi*(1:1000)'*3/(1000+1))

lbs = "Sine";

% subplot(2,1,kj)
for kj= 1:5
    subplot(5,1,kj)
    plot(sine_tprs_array(:,kj))
    title(lbs)
    legend(append('k = ',string(kj)), ...
        'Orientation','horizontal','Location','south')
    legend('boxoff')
    ylim([-0.09 0.07])
end

6.2 计算是否符合正交

sine_tprs_array = tprs(:,:,2);
rslt = zeros([5,5]);
for i =1:5
    for j = 1:5
        rslt(i,j) = sine_tprs_array(:,i)'*sine_tprs_array(:,j); % 计算向量积，检查是否正交
    end
end`

>> rslt

rslt =

    1.0000    0.0000   -0.0000   -0.0000    0.0000
    0.0000    1.0000   -0.0000    0.0000   -0.0000
   -0.0000   -0.0000    1.0000   -0.0000   -0.0000
   -0.0000    0.0000   -0.0000    1.0000   -0.0000
    0.0000   -0.0000   -0.0000   -0.0000    1.0000
% 可见这几个窗函数都是正交的。

7. Reference

1. Multitaper power spectral density estimate - MATLAB pmtm
2. 频谱分析中如何理解taper？ - 知乎
3. [数字信号中功率谱估计相关方法简介及MATLAB实现_matlab功率谱
4. The multi-taper method - YouTube