docker中镜像的作用

镜像原理
镜像

镜像到底是什么？镜像是一种轻量级、可执行的独立软件包，用来打包软件运行环境和基于运行环境开发的软件，它包含运行某个软件所需的所有内容，包括代码、运行时、库、环境变量和配置文件。
1.UnionFS（联合文件系统）：

Union文件系统（UnionFS）是一种分层、轻量级并且高性能的文件系统，它支持对文件系统的修改作为一次提交来一层层的叠加，同时可以将不同目录挂载到同一个虚拟文件系统下(unite several directories into a single virtual filesystem)。

UnionFS是docker镜像的基础

UnionFS特性：
一次同时加载多个文件系统，但从外面看起来，只能看到一个文件系统，联合加载会把各层文件系统叠加起来，这样最终的文件系统会包含所有底层的文件和目录
2.Docker镜像的加载原理

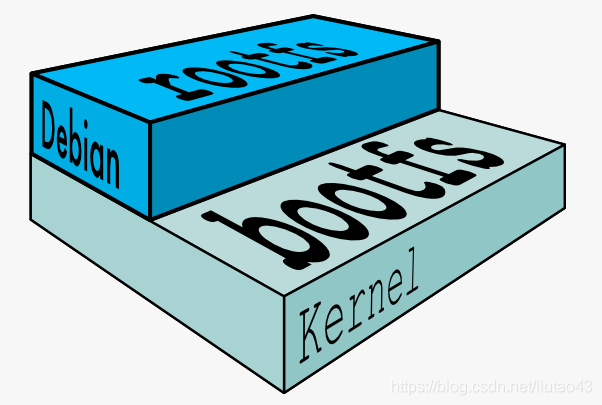
docker的镜像实际上由一层一层的文件系统组成，这种层级的文件系统UnionFS。

bootfs(boot file system)主要包含bootloader和kernel, bootloader主要是引导加载kernel, Linux刚启动时会加载bootfs文件系统，在Docker镜像的最底层是bootfs。这一层与我们典型的Linux/Unix系统是一样的，包含boot加载器和内核。当boot加载完成之后整个内核就都在内存中了，此时内存的使用权已由bootfs转交给内核，此时系统也会卸载bootfs。

rootfs (root file system) ，在bootfs之上。包含的就是典型 Linux 系统中的 /dev, /proc, /bin, /etc 等标准目录和文件。rootfs就是各种不同的操作系统发行版，比如Ubuntu，Centos等等。

虚拟化中的镜像分为：

3.Docker镜像层

平时我们安装进虚拟机的CentOS都是好几个G，为什么docker这里才200M？？
对于一个精简的OS，rootfs可以很小，只需要包括最基本的命令、工具和程序库就可以了，因为底层直接用Host的kernel，自己只需要提供 rootfs 就行了。由此可见对于不同的linux发行版, bootfs基本是一致的, rootfs会有差别, 因此不同的发行版可以公用bootfs。

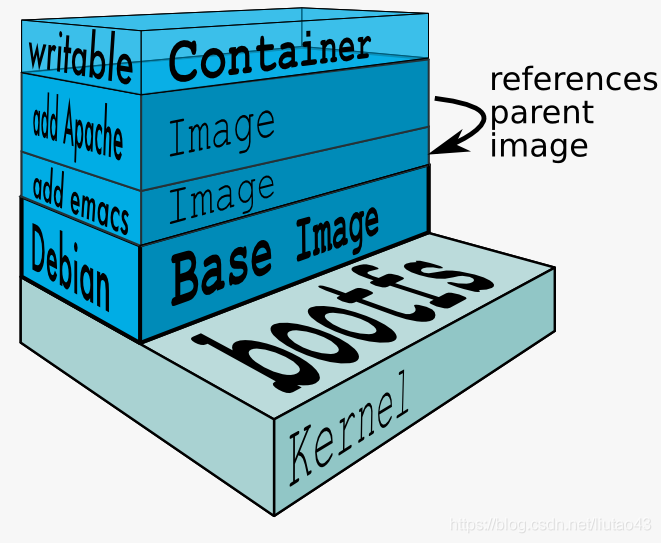
每一个镜像都可能依赖于由一个或多个下层的组成的另一个镜像。我们有时说，下层那个 镜像是上层镜像的父镜像。一个没有任何父镜像的镜像，谓之基础镜像。

docker pull就是将镜像一层一层加载:

一个mongodb的镜像如下：

4.为什么Docker镜像要采用这种分层结构呢？

最大的一个好处就是 - 共享资源
比如：有多个镜像都从相同的 base 镜像构建而来，那么宿主机只需在磁盘上保存一份base镜像，同时内存中也只需加载一份 base 镜像，就可以为所有容器服务了。而且镜像的每一层都可以被共享。
5.特点

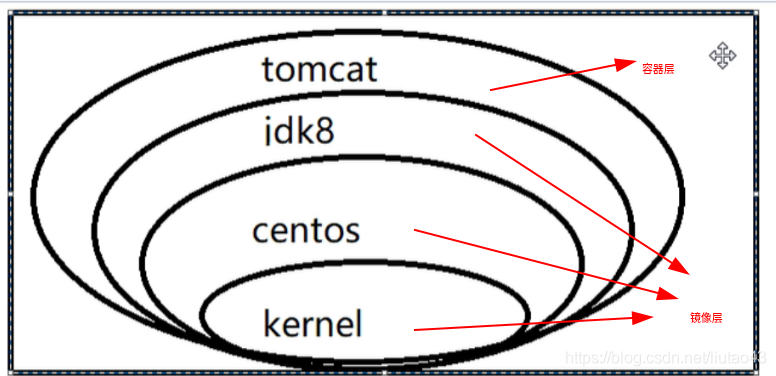
Docker镜像都是只读的，当容器启动时，一个新的可写层被加载到镜像的顶部。这一层通常被称为“容器层”。“容器层”之下的都叫“镜像层”

Docker制作镜像

通过容器制作镜像

Docker commit 命令

docker commit :从容器创建一个新的镜像。

语法

docker commit [OPTIONS] CONTAINER [REPOSITORY[:TAG]]
OPTIONS说明：

-a :提交的镜像作者；

-c :使用Dockerfile指令来创建镜像；

-m :提交时的说明文字；

-p :在commit时，将容器暂停。

实例

将容器a404c6c174a2 保存为新的镜像,并添加提交人信息和说明信息。

原文链接：https://blog.csdn.net/liutao43/article/details/109384085