Solution -「CF 1380F」Strange Addition

\(\mathcal{Description}\)

  Link.

  定义两个数在进行加法时，进位单独作为一位。例如:

.

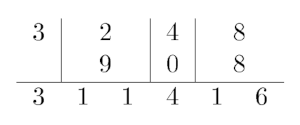  给定一个 \(n\) 为数和 \(m\) 次修改操作，每次修改会修改 \(n\) 位数的某一位数字。在每次修改后求出有多少对数以上述规则相加后的得数为这个 \(n\) 为数。

  \(n,m\le5 \times 10^5\)。

\(\mathcal{Solution}\)

  显然的 DDP。

  令 \(f_i\) 表示加和为目标数后 \(i\) 为数字的数对数量。那么：

\[ w_{i+1}
\begin{pmatrix}
f_i\\
f_{i-1}
\end{pmatrix}
=
\begin{pmatrix}
f_{i+1}\\
f_i
\end{pmatrix}
\]

  其中 \(w_i~(i=1,2,\dots,18)\) 分别表示每种“一位数”的转移矩阵，只有 \(i=1\) 需要特殊处理。

  具体看代码吧（摊手。

\(\mathcal{Code}\)

/* Clearink */

#include <cstdio>

inline int rint () {
	int x = 0, f = 1; char s = getchar ();
	for ( ; s < '0' || '9' < s; s = getchar () ) f = s == '-' ? -f : f;
	for ( ; '0' <= s && s <= '9'; s = getchar () ) x = x * 10 + ( s ^ '0' );
	return x * f;
}

template<typename Tp>
inline void wint ( Tp x ) {
	if ( x < 0 ) putchar ( '-' ), x = ~ x + 1;
	if ( 9 < x ) wint ( x / 10 );
	putchar ( x % 10 ^ '0' );
}

const int MAXN = 5e5, MOD = 998244353;
const int w[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 };
int n, m;
char num[MAXN + 5];

inline int add ( int a, const int b ) { return ( a += b ) < MOD ? a : a - MOD; }
inline int mul ( long long a, const int b ) { return ( a *= b ) < MOD ? a : a % MOD; }

struct Matrix {
	int mat[2][2];
	Matrix (): mat {} {}
	Matrix ( const int a, const int b, const int c, const int d ):
		mat { a, b, c, d } {}

	inline int* operator [] ( const int key ) { return mat[key]; }

	inline Matrix operator * ( Matrix& t ) const {
		Matrix ret;
		for ( int i = 0; i < 2; ++ i ) {
			for ( int k = 0; k < 2; ++ k ) {
				for ( int j = 0; j < 2; ++ j ) {
					ret[i][j] = add ( ret[i][j], mul ( mat[i][k], t[k][j] ) );
				}
			}
		}
		return ret;
	}

	inline void _show () const {
#ifdef RYBY
		for ( int i = 0; i < 2; ++ i ) {
			for ( int j = 0; j < 2; ++ j ) {
				printf ( "%d ", mat[i][j] );
			}
			putchar ( '\n' );
		}
#endif
	}
};

inline Matrix digit ( const int d ) {
	return Matrix ( w[num[d] - '0'], num[d] ^ '1' || d == n ? 0 : w[10 + num[d + 1] - '0'], 1, 0 );
}

struct SegmentTree {
	Matrix mat[MAXN * 2 + 5];

	inline int id ( const int l, const int r ) { return ( l + r ) | ( l != r ); }

	inline int build ( const int l, const int r ) {
		int rt = id ( l, r ), mid = l + r >> 1;
		if ( l == r ) return ( mat[rt] = digit ( l ) )._show (), rt;
		int lc = build ( l, mid ), rc = build ( mid + 1, r );
		return mat[rt] = mat[lc] * mat[rc], rt;
	}

	inline void update ( const int l, const int r, const int x, const char d ) {
		int rt = id ( l, r ), mid = l + r >> 1;
		if ( l == r ) return num[l] = d, mat[rt] = digit ( l ), void ();
		if ( x <= mid ) update ( l, mid, x, d );
		else update ( mid + 1, r, x, d );
		mat[rt] = mat[id ( l, mid )] * mat[id ( mid + 1, r )];
	}
} segt;

int main () {
	n = rint (), m = rint ();
	scanf ( "%s", num + 1 );
	int rt = segt.build ( 1, n );
	for ( int x, d; m --; ) {
		x = rint (), d = rint ();
		segt.update ( 1, n, x, d ^ '0' );
		if ( x > 1 ) segt.update ( 1, n, x - 1, num[x - 1] );
		segt.mat[rt]._show ();
		wint ( segt.mat[rt][0][0] ), putchar ( '\n' );
	}
	return 0;
}