LeetCode 887. Super Egg Drop

题目链接：https://leetcode.com/problems/super-egg-drop/

题意：给你K个鸡蛋以及一栋N层楼的建筑，已知存在某一个楼层F(0<=F<=N)，在不高于F的楼层扔鸡蛋不会碎，鸡蛋碎了不能再用，没碎可以继续使用，问不论F的大小(0<=F<=N)，至少需要测量多少次才能测出F的大小。题意挺好理解的，鸡蛋少的话操作肯定多点，相当于行下往上测，鸡蛋比较多就可以使用类似二分的想法了。

思路1:

　　dp+二分  时间复杂度O(K*N*log N)，空间复杂度O(K*N)  (自己第一次想的就是这个思路630ms，能过但是慢)

　　假设我们有i个鸡蛋，我们从x层楼扔下去，如果碎了，说明F<x，相当于使用i-1个鸡蛋测量j-1层至少要测试多少次，个数加1即为答案；没碎，说明F>x，则我们使用i个鸡蛋测量x+1~N的楼层至少需要操作多少次，即N-x个楼层，下面的楼层不同考虑。二者的答案取较大的值即可。

　　因此dp的思想就很明显了dp[i][j]表示使用i个鸡蛋测量j个楼层至少需要操作的次数，则dp[i][j] =min( max(dp[i-1][x-1],dp[i][j-x])+1 ,(x<=j)).

　　该算法的复杂度是O(K*N^2),交上去应该会TLE

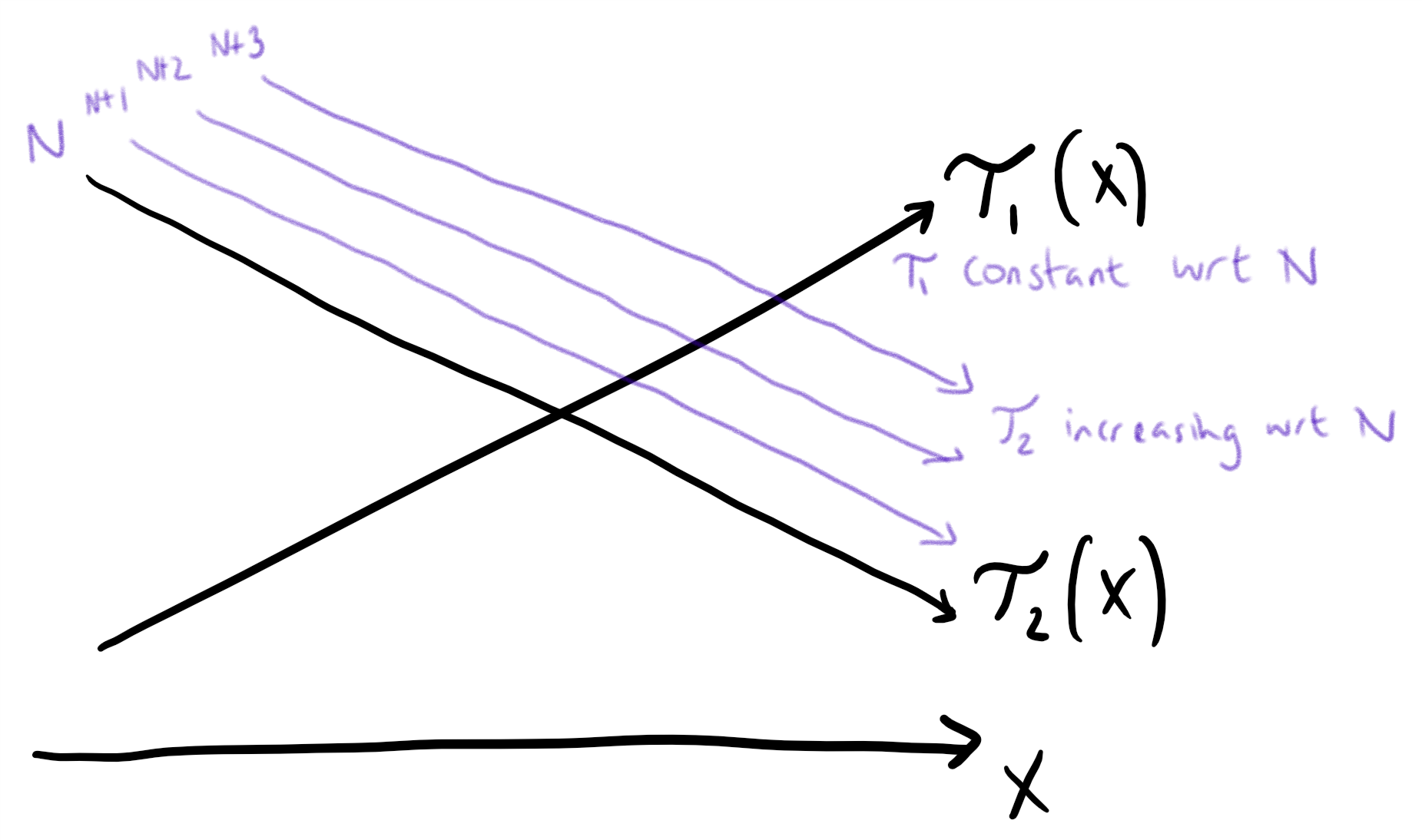
　　通过观察我们可以发现dp[i-1][x-1]是随着x的增大而增大（或者不变）的（相同的鸡蛋数层数越多肯定测试次数也越多），同理dp[i][j-x]随着x的增大而减小的，而现在我们要求对于每个x，这两个数的较大值，最后再在这j个值中取一个较小值。如果是连续函数的话，就相当于求两条曲线高的那部分的最小值。如下图所示（图来自leetcode），求的是蓝色部分的最小值。所以我们可以通过二分求出二者“交点“（交点可能不存在）附近的那两个值，答案肯定是这两个值中的一个。所以降了一维，复杂度变为O(K*N*log N)。

class Solution {
public:
    int superEggDrop(int K, int N) {
        int dp[101][10001];
        memset(dp,0,sizeof(dp));
        for(int i=1;i<=K;i++)
            for(int j=1;j<=N;j++){
                dp[0][j]=1e9;
                dp[i][j]=1e9;
                int l=1,r=j;
                int mid;
                for(int k=1;k<=20;k++){
                     mid=(l+r)/2;
                    if(dp[i-1][mid-1]<dp[i][j-mid])
                        l=mid;
                    else r=mid;
                }
                 if(dp[i-1][mid-1]<=dp[i][j-mid])
                     mid++;
                dp[i][j]=min(dp[i-1][mid-1],dp[i][j-(mid-1)])+1;
            }
        return dp[K][N];
    }
};　　

思路2：

　　dp方程仍然是思路一中的方程，但是对于dp[i][j-x]，随着j增大，最优值x的取值也会增大，即下图中的交点，既然x是非递减的，不需要每次都遍历了，因此复杂度可以减少到O(N*K)

class Solution {
public:
    int superEggDrop(int K, int N) {
        int dp[101][10001];
        memset(dp,0,sizeof(dp));
        for(int i=1;i<=K;i++){
            int x=1;
            for(int j=1;j<=N;j++){
                dp[0][j]=1e9;
                dp[i][j]=1e9;
                while(x<j&&max(dp[i-1][x-1],dp[i][j-x])>max(dp[i-1][x],dp[i][j-x-1]))
                    x++;
                dp[i][j]=max(dp[i-1][x-1],dp[i][j-x])+1;
            }
        }
        return dp[K][N];
    }
};

　　空间复杂度也可以利用循环数组降低到O(N):

class Solution {
public:
    int superEggDrop(int K, int N) {
        int dp[2][10001];
        memset(dp,0,sizeof(dp));
        int cnt=0;
        for(int j=1;j<=N;j++)
            dp[0][j] = dp[1][j] = 1e9;
        for(int i=1;i<=K;i++){
            int x = 1;
            for(int j=1;j<=N;j++){
                while(x<j&&max(dp[cnt^0][x-1],dp[cnt^1][j-x])>max(dp[cnt^0][x],dp[cnt^1][j-x-1]))
                    x++;
                dp[cnt^1][j]=max(dp[cnt^0][x-1],dp[cnt^1][j-x])+1;
            }
            cnt=cnt^1;
        }
        return dp[cnt^0][N];
    }
};

思路3：

　　我们改变一下dp方程，dp[i][j]表示使用i个鸡蛋，j次操作，能够测量的最高楼层，假设我们采用最优策略，则对于第j次操作如果鸡蛋碎了，则需要使用i-1个鸡蛋，j-1次操作测量该层下面的楼层；如果鸡蛋没碎，则需要使用i个鸡蛋，j-1次操作测试上面的楼层，因此dp[i][j] = dp[i-1][j-1] + dp[i][j-1] + 1，我们需要找到最小的j使得dp[i][j]>=N 复杂度O(K*log N) （由于是找最小的j，因此外层循环是j）

class Solution {
public:
	int superEggDrop(int K, int N) {
		int **dp = new int *[K + 1];
		for (int i = 0;i <= K;i++) {
			dp[i] = new int[N + 1];
			memset(dp[i], 0, 4 * (N + 1));
		}
		for (int j = 1;j<=N;j++)
			for (int i = 1;i <= K;i++) {
				dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1] + 1;
				if (dp[i][j] >= N)
					return j;
			}
		return N;
	}
};