数据结构(c++)(第二版) Dijkstra最短路径算法 教学示范代码出现重大问题！

前言

去年在数据结构(c++)的Dijkstra教学算法案例中，发现了一个 bug 导致算法不能正常的运行，出错代码只是4行的for循环迭代代码。

看到那里就觉得有问题，但书中只给了关键代码的部分，其余皆是伪代码，做伪代码实现，运行了教学代码，证实了相关错误。也给出了能正确运行的for循环迭代代码。

之后便将过程发给出版社，可一年多了，出版社也没有回信......

也希望大家也可以讨论一下。

Dijkstra最短路径算法

Dijkstra最路径算法用于求单源点最短路径问题，问题描述如下：给定带权有向图G=(V,E)和源点v属于V，求从v到G中其余各顶点的最短路径。

单源点最短路径问题的一个应用实例是关于计算机网络传输的问题：怎样找到一种最经济的方式，从一台计算机向网上所有其他计算机发送一条消息。

Dijkstra算法是应用贪心法进行算法设计的一个典型例子。

问题

数据结构(c++)(第二版) 版次：2011年6月第2版 印次：2020年1月第25次印刷 清华大学出版社

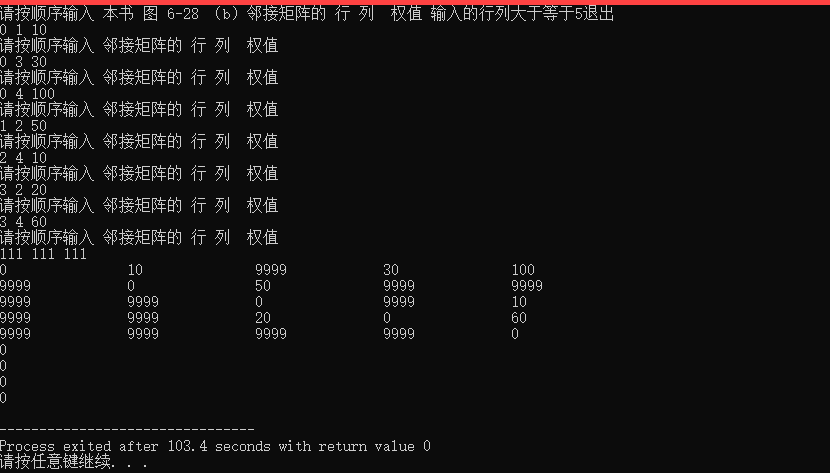
书中的Dijkstra的实列代码(P170-171)出现了'k'无法更新的错误，代码无法得到最后的正确结果。

'k'是dist[n]中最小值的下标，所以每次'k'的更新都要从S集合之外去寻找，而书中是以 k=0 去更新，在k=0的条件约束下，根本无法进入k的更新，所以在运行了4次之后会退出while() 没有办法更新。

希望贵出版社能够思考，若确实有错误希望贵出版社能够修正此代码。

#include <iostream>
#include <cstring>
using namespace std;
const int Max=9999;
class MGraph
{
	int arc[5][5];		//邻接矩阵
	string vertex[10];	//图的顶点
	int vertexNum;
public:
	MGraph();				//初始化邻接矩阵 对角元素为0 其他元素为Max
	void Input();      		//输入书中的 6 -28 进行测试
	void Show();
	friend void Dijkastra( MGraph G , int v );
};
MGraph::MGraph()
{
	int i,j;
	vertexNum=5;
	vertex[0]='a';    //等同于 V0
	vertex[1]='b';
	vertex[2]='c';
	vertex[3]='d';
	vertex[4]='e';
	vertex[5]='\0';
	for(i=0;i<5;i++)
	{
		for(j=0;j<5;j++)
		{
			arc[i][j]=Max;
			if(i==j) arc[i][j]=0;
		}
	}
}
void MGraph::Input()
{
	int i,j,d;
	cout<<"请按顺序输入 本书 图 6-28 （b）邻接矩阵的 行 列  权值 输入的行列大于等于5退出"<<endl;
	cin>>i>>j>>d;
	while((i<5)&&(j<5))
	{
		arc[i][j]=d;
		cout<<"请按顺序输入 邻接矩阵的 行 列  权值"<<endl;
		cin>>i>>j>>d;
	}
}
void MGraph::Show()
{
	int i,j;
    for(i=0;i<5;i++)
    {
        for(j=0;j<5;j++)
        {
            cout<<arc[i][j]<<"		";
        }
        cout<<endl;
    }
}
void Dijkastra( MGraph G , int v )
{
	int i=0,k;
	int dist[10];
	int s[5];
	int num;
	string path[10];
	for (i=0; i<G.vertexNum; i++)
	{
		dist[i]=G.arc[v][i];
		if (dist[i]!=Max) path[i]=G.vertex[v]+G.vertex[i];
		else path[i]="";
	}
	s[0]=v;			//初始化集合 S
	dist[v]=0;		//标记顶点 v 为源点
	num=1;
	while(num<G.vertexNum)					//当顶点数num小于图的顶点数
	{
		// 使用时 这两个for循环使用其中一个 即可得到对应结果
		// 可以成功实现的迭代代码
		/*for(i=0;i<G.vertexNum;i++)       		//修改后的 k 的迭代    *************************************
		{
			if(dist[i]!=0)
			{
				k=i;
				break;
			}
		}*/
		// 书中的教学代码
		for(i=0;i<G.vertexNum;i++) 		//在dist中查找最小元素        ** k 无法更新！
		{
			if((dist[i]!=0)&&(dist[i]<dist[k])) k=i;
		}
		cout<<dist[k]<<" "<<path[k]<<endl;
		s[num++]=k;							//将生成的重点加入集合S
		for(i=0;i<G.vertexNum;i++)			//修改数组dist和path
		{
			if(dist[i]>dist[k]+G.arc[k][i])
			{
				dist[i]=dist[k]+G.arc[k][i];
				path[i]=path[k]+G.vertex[i];
			}
		}
		dist[k]=0;		//置顶点k 为已生成顶点标记
	}
}
int main(int argc, char** argv)
{
	MGraph G;
	G.Input();
	G.Show();
	Dijkastra(G,0);
	return 0;
}

改正后的代码

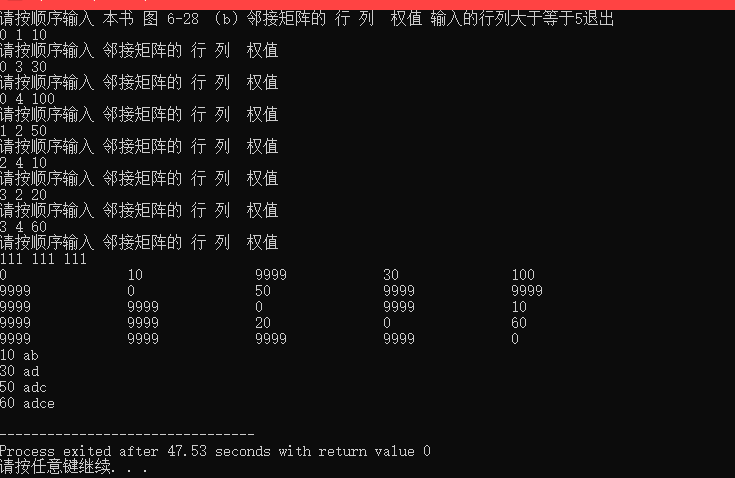
教材示例代码