机器学习——softmax回归

softmax回归

　　前面介绍了线性回归模型适用于输出为连续值的情景。在另一类情景中，模型输出可以是一个像图像类别这样的离散值。对于这样的离散值预测问题，我们可以使用诸如 softmax 回归在内的分类模型。和线性回归不同，softmax 回归的输出单元从一个变成了多个，且引入了 softmax 运算使输出更适合离散值的预测和训练。本节以 softmax 回归模型为例，介绍神经网络中的分类模型。

1 分类问题

　　让我们考虑一个简单的图像分类问题，其输入图像的高和宽均为2像素，且色彩为灰度。这样每个像素值都可以用一个标量表示。我 们将图像中的4像素分别记为 $x_{1}, x_{2}, x_{3}, x_{4} $ 。假设训练数据集中图像的真实标签为狗、猫或鸡（假设可以用4像素表示出这3种动物），这些标签分别对应离散值 $y_{1}, y_{2}, y_{3}$ 。
　　我们通常使用离散的数值来表示类别，例如 $y_{1}=1, y_{2}=2, y_{3}=3$ 。如此，一张图像的标签为 1、2 和 3 这 3 个数值中的一个。虽然 我们仍然可以使用回归模型来进行建模，并将预测值就近定点化到 1、2 和 3 这 3 个离散值之一，但这种连续值到离散值的转化通常会 影响到分类质量。因此我们一般使用更加适合离散值输出的模型来解决分类问题。

2 softmax回归模型

　　softmax回归跟线性回归一样将输入特征与权重做线性叠加。与线性回归的一个主要不同在于，softmax 回归的输出值个数等于标签里的类别数。因为一共有4种特征和3种输出动物类别，所以权重包含12个标量（带下标的 $w$ ）、偏差包含3个标量（带下标的 $b$ ），且对每个输入计算 $o_1,o_2,o_3 $ 这 3 个输出：

　　　　$\begin{aligned} 　　　　o_1 &= x_1 w_{11} + x_2 w_{21} + x_3 w_{31} + x_4 w_{41} + b_1,\\ 　　　　o_2 &= x_1 w_{12} + x_2 w_{22} + x_3 w_{32} + x_4 w_{42} + b_2,\\ 　o_3 &= x_1 w_{13} + x_2 w_{23} + x_3 w_{33} + x_4 w_{43} + b_3. 　　　　\end{aligned}$

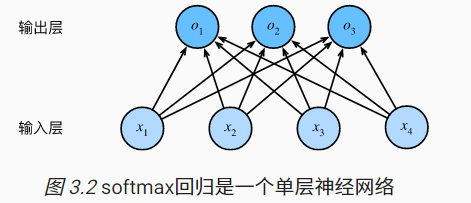
　　图3.2用神经网络图描绘了上面的计算。softmax 回归同线性回归一样，也是一个单层神经网络。由于每个输出 $o_{1}, o_{2}, o_{3}$ 的计算都要依赖于所有的输入 $x_{1}, x_{2}, x_{3}, x_{4}$, softmax回归的输出层也是一个全连接层。
　　　　

3 softmax运算

　　既然分类问题需要得到离散的预测输出，一个简单的办法是将输出值 $o_{i}$ 当作预测类别是 $i $ 的置信度, 并将值最大的输出所对应的类作为预测输出，即输出 $\underset{i}{argmax} \  o_{i} $ 。 例如，如果 $o_{1}, o_{2}, o_{3} $ 分别为 $ 0.1,10,0.1$ , 由于 $o_{2}$ 最大, 那么预测类别为 $2$，其代表猫。
　　然而，直接使用输出层的输出有两个问题。一方面，由于输出层的输出值的范围不确定，我们难以直观上判断这些值的意义。例如，刚才举的例子中的输出值 $10$ 表示“很置信"图像类别为猫，因为该输出值是其他两类的输出值的 $100$ 倍。但如果 $o_{1}=o_{3}=10^{3}$ 绑么输出值 $10$ 却又表示图像类别为猫的概率很低。另一方面，由于真实标签是离散值，这些离散值与不确定范围的输出值之间的误差难以衡量。
　　softmax运算符（softmax operator）解决了以上两个问题。它通过下式将输出值变换成值为正且和为 $1$ 的概率分布：

　　　　$\hat{y}_1, \hat{y}_2, \hat{y}_3 = \text{softmax}(o_1, o_2, o_3),$

　　其中
$${\large \hat{y}_1 = \frac{ \exp(o_1)}{\sum_{i=1}^3 \exp(o_i)},\quad
\hat{y}_2 = \frac{ \exp(o_2)}{\sum_{i=1}^3 \exp(o_i)},\quad
\hat{y}_3 = \frac{ \exp(o_3)}{\sum_{i=1}^3 \exp(o_i)}.} $$
　　容易看出 $\hat{y}_1 + \hat{y}_2 + \hat{y}_3 = 1$ 且 $0 \leq \hat{y}_1, \hat{y}_2, \hat{y}_3 \leq 1$ ，因此 $\hat{y}_1, \hat{y}_2, \hat{y}_3$ 是一个合法的概率分布。这时候，如果 $\hat{y}_2=0.8$ ，不管 $\hat{y}_1$ 和 $\hat{y}_3$ 的值是多少，我们都知道图像类别为猫的概率是 80%。此外，我们注意到
　　　　$\underset{i}{argmax} \  o_i = \underset{i}{argmax} \ \hat y_i,$
　　因此softmax运算不改变预测类别输出。

4 单样本分类的矢量计算表达式

　　为了提高计算效率，我们可以将单样本分类通过矢量计算来表达。在上面的图像分类问题中，假设softmax回归的权重和偏差参数分别为

$$\begin{split}\boldsymbol{W} =
\begin{bmatrix}
w_{11} & w_{12} & w_{13} \\
w_{21} & w_{22} & w_{23} \\
w_{31} & w_{32} & w_{33} \\
w_{41} & w_{42} & w_{43}
\end{bmatrix},\quad
\boldsymbol{b} =
\begin{bmatrix}
b_1 & b_2 & b_3
\end{bmatrix},\end{split}$$

　　设高和宽分别为2个像素的图像样本 $i$ 的特征为
　　　　\begin{aligned} \boldsymbol{x}^{(i)} = \begin{bmatrix}x_1^{(i)} & x_2^{(i)} & x_3^{(i)} & x_4^{(i)}\end{bmatrix} \end{aligned}
　　输出层的输出为
　　　　\begin{aligned}  \boldsymbol{o}^{(i)} = \begin{bmatrix}o_1^{(i)} & o_2^{(i)} & o_3^{(i)}\end{bmatrix} \end{aligned}
　　预测为狗、猫或鸡的概率分布为
　　　　\begin{aligned}   \boldsymbol{\hat{y}}^{(i)} = \begin{bmatrix}\hat{y}_1^{(i)} & \hat{y}_2^{(i)} & \hat{y}_3^{(i)}\end{bmatrix}   \end{aligned}
　　softmax回归对样本 $ i $ 分类的矢量计算表达式为
　　\begin{split}\begin{aligned}
　　\boldsymbol{o}^{(i)} &= \boldsymbol{x}^{(i)} \boldsymbol{W} + \boldsymbol{b},\\
　　\boldsymbol{\hat{y}}^{(i)} &= \text{softmax}(\boldsymbol{o}^{(i)}).
　　\end{aligned}\end{split}

5 小批量样本分类的矢量计算表达式

　　为了进一步提升计算效率，我们通常对小批量数据做矢量计算。广义上讲，给定一个小批量样本，其批量大小为 $ n$ , 输入个数（特 征数）为  $d$ , 输出个数（类别数）为  $q_{\circ} $ 设批量特征为  $\boldsymbol{X} \in \mathbb{R}^{n \times d} $ 。假设 softmax 回归的权重和偏差参数分别为  $\boldsymbol{W} \in \mathbb{R}^{d \times q}$  和  $\boldsymbol{b} \in \mathbb{R}^{1 \times q}$ 。 $ \operatorname{softmax} $ 回归的矢量计算表达式为

\begin{split}\begin{aligned}
\boldsymbol{O} &= \boldsymbol{X} \boldsymbol{W} + \boldsymbol{b},\\
\boldsymbol{\hat{Y}} &= \text{softmax}(\boldsymbol{O}),
\end{aligned}\end{split}

　　其中的加法运算使用了广播机制，$\boldsymbol{O}, \boldsymbol{\hat{Y}} \in \mathbb{R}^{n \times q}$ 且这两个矩阵的第 $i$ 行分别为样本 $i$ 的输出 $\boldsymbol{o}^{(i)}$ 和概率分布 $\boldsymbol{\hat{y}}^{(i)}$.

6 交叉熵损失函数

　　前面提到，使用softmax运算后可以更方便地与离散标签计算误差。我们已经知道， softmax 运算将输出变换成一个合法的类别预测分布。实际上，真实标签也可以用类别分布表达：对于样本 $ i $ , 我们构造向量 $ \boldsymbol{y}^{(i)} \in \mathbb{R}^{q} $ , 使其第 $y^{(i)} $ (样本 $i $ 类别的离散数值）个元素为 $1 $, 其余为 $0$ 。 这样我们的训练目标可以设为使预测概率分布 $ \hat{\boldsymbol{y}}^{(i)}$ 尽可能接近真实的标签概率分布 $\boldsymbol{y}^{(i)} $ 。
　　我们可以像线性回归那样使用平方损失函数 $\left\|\hat{\boldsymbol{y}}^{(i)}-\boldsymbol{y}^{(i)}\right\|^{2} / 2$ 。然而，想要预测分类结果正确，我们其实并不需要预测概率完全等 于标签概率。例如, 在图像分类的例子里, 如果 $y^{(i)}=3$ , 那么我们只需要 $ \hat{y}_{3}^{(i)}$ 比其他两个预测值 $ \hat{y}_{1}^{(i)} $ 和 $\hat{y}_{2}^{(i)}$ 大就行了。即使 $\hat{y}_{3}^{(i)} $ 值 为 $0.6$ , 不管其他两个预测值为多少, 类别预测均正确。而平方损失则过于严格，例如 $\hat{y}_{1}^{(i)}=\hat{y}_{2}^{(i)}=0.2$ 比 $\hat{y}_{1}^{(i)}=0, \hat{y}_{2}^{(i)}=0.4$ 的 损失要小很多, 虽然两者都有同样正确的分类预测结果。
　　改善上述问题的一个方法是使用更适合衡量两个概率分布差异的测量函数。其中, 交叉嫡（cross entropy）是一个常用的衡量方法：

　　　　$H\left(\boldsymbol y^{(i)}, \boldsymbol {\hat y}^{(i)}\right ) = -\sum_{j=1}^q y_j^{(i)} \log \hat y_j^{(i)}$

　　其中带下标的 $y_{j}^{(i)}$ 是向量 $ \boldsymbol{y}^{(i)} $ 中非 0 即 1 的元素，需要注意将它与样本 $i$ 类别的离散数值，即不带下标的 $y^{(i)}$ 区分。在上式中，我们知道向量 $\boldsymbol{y}^{(i)}$ 中只有第 $y^{(i)} $ 个元素 $ y_{y^{(i)}}^{(i)} $ 为 1, 其余全为0, 于是 $H(\boldsymbol y^{(i)}, \boldsymbol {\hat y}^{(i)}) = -\log \hat y_{y^{(i)}}^{(i)}$ 也就是说，交叉熵只关心对正确类别的预测概率，因为只要其值足够大，就可以确保分类结果正确。当然，遇到一个样本有多个标签时，例如图像里含有不止一个物体时， 我们并不能做这一步简化。但即便对于这种情况，交叉熵同样只关心对图像中出现的物体类别的预测概率。
　　假设训练数据集的样本数为 $ n$ , 交叉熵损失函数定义为

　　$\begin{aligned} \ell(\boldsymbol{\Theta}) = \frac{1}{n} \sum_{i=1}^n H\left(\boldsymbol y^{(i)}, \boldsymbol {\hat y}^{(i)}\right ) \end{aligned}$

　　其中 \boldsymbol{\Theta} 代表模型参数。同样地，如果每个样本只有一个标签, 那么交叉燈损失可以简写成 $\ell(\boldsymbol{\Theta}) = -(1/n) \sum \limits _{i=1}^n \log \hat y_{y^{(i)}}^{(i)}$ 从另一个角度来看，我们知道最小化 $\ell(\boldsymbol{\Theta})$ 等价于最大化 $\exp(-n\ell(\boldsymbol{\Theta}))=\prod \limits_{i=1}^n \hat y_{y^{(i)}}^{(i)}$ , 即最小化交叉嫡损失函数等价于最大化训练数 据集所有标签类别的联合预测概率。

7 模型预测及评价

　　在训练好softmax回归模型后，给定任一样本特征，就可以预测每个输出类别的概率。通常，我们把预测概率最大的类别作为输出类别。如果它与真实类别（标签）一致，说明这次预测是正确的。在之后“softmax回归的从零开始实现”一节的实验中，我们将使用准确率（accuracy）来评价模型的表现。它等于正确预测数量与总预测数量之比。

8 小结

• softmax回归适用于分类问题。它使用softmax运算输出类别的概率分布。
• softmax回归是一个单层神经网络，输出个数等于分类问题中的类别个数。
• 交叉熵适合衡量两个概率分布的差异。