中龙技术 | HSCSEC CRY + MISC WP
CRYPTO[HSC-1th]
Easy SignIn
5445705857464579517A4A48546A4A455231645457464243566B5579556C7053546C4A4E524564565646644D515670455130354C5755644F5231685256314A5452315A5552304E57576C5A49525430395054303950513D3D
Cyber一把梭

RSA
import gmpy2
import sympy
from Crypto.Util.number import *
flag = b'????'
z=getPrime(1024)
p=sympy.nextprime(z)
q=sympy.prevprime(10*z)
n=p*q
m=bytes_to_long(flag)
e=0xe18e
c=pow(m,e,n)
print("n=",n)
print("c=",c)
#n= 124689085077258164778068312042204623310499608479147230303784397390856552161216990480107601962337145795119702418941037207945225700624828698479201514402813520803268719496873756273737647275368178642547598433774089054609501123610487077356730853761096023439196090013976096800895454898815912067003882684415072791099101814292771752156182321690149765427100411447372302757213912836177392734921107826800451961356476403676537015635891993914259330805894806434804806828557650766890307484102711899388691574351557274537187289663586196658616258334182287445283333526057708831147791957688395960485045995002948607600604406559062549703501
#c= 57089349656454488535971268237112640808678921972499308620061475860564979797594115551952530069277022452969364212192304983697546604832633827546853055947447207342333989645243311993521374600648715233552522771885346402556591382705491510591127114201773297304492218255645659953740107015305266722841039559992219190665868501327315897172069355950699626976019934375536881746570219967192821765127789432830133383612341872295059056728626931869442945556678768428472037944494803103784312535269518166034046358978206653136483059224165128902173951760232760915861623138593103016278906012134142386906130217967052002870735327582045390117565考点:费马分解 + 罗宾
gcd(e,φ(n)) = 2, 设e' = e/2 ,m' = m2 , 求出 m ′ 再利用Rabin求 m 。
EXP
n= 124689085077258164778068312042204623310499608479147230303784397390856552161216990480107601962337145795119702418941037207945225700624828698479201514402813520803268719496873756273737647275368178642547598433774089054609501123610487077356730853761096023439196090013976096800895454898815912067003882684415072791099101814292771752156182321690149765427100411447372302757213912836177392734921107826800451961356476403676537015635891993914259330805894806434804806828557650766890307484102711899388691574351557274537187289663586196658616258334182287445283333526057708831147791957688395960485045995002948607600604406559062549703501
c= 57089349656454488535971268237112640808678921972499308620061475860564979797594115551952530069277022452969364212192304983697546604832633827546853055947447207342333989645243311993521374600648715233552522771885346402556591382705491510591127114201773297304492218255645659953740107015305266722841039559992219190665868501327315897172069355950699626976019934375536881746570219967192821765127789432830133383612341872295059056728626931869442945556678768428472037944494803103784312535269518166034046358978206653136483059224165128902173951760232760915861623138593103016278906012134142386906130217967052002870735327582045390117565
e = 0xe18e
import gmpy2
p = gmpy2.iroot(n//10,2)[0]
while 1:
p = gmpy2.next_prime(p)
if n%p==0:
break
q = n//p
f = (p-1)*(q-1)
d = gmpy2.invert(e//2,f)
mm = pow(c,d,n)
print(mm)
def rabin_decrypt(c, p, q, e=2):
n = p * q
mp = pow(c, (p + 1) // 4, p)
mq = pow(c, (q + 1) // 4, q)
yp = gmpy2.invert(p, q)
yq = gmpy2.invert(q, p)
r = (yp * p * mq + yq * q * mp) % n
rr = n - r
s = (yp * p * mq - yq * q * mp) % n
ss = n - s
return (r, rr, s, ss)
m = rabin_decrypt(mm,p,q)
for i in range(4):
try:
print(bytes.fromhex(hex(m[i])[2:]))
except:
pass
# b'flag{6d22773623d3d5c871692e9985de5f16}'AFFINE
查看代码
# -*- coding: utf-8 -*-
import string
import hashlib
letter=string.ascii_letters+string.digits
def encrypt(m, c, a, b):
for i in range(len(m)):
ch=m[i]
t=(letter.index(ch) * a + b) % 62
c.append(letter[t])
d = ''.join(c)
print(d)
m =
c = []
a =
b =
assert ("flag" in m)
print("加密后的密文为:")
Cipher = encrypt(m, c, a, b)
flag = hashlib.md5("".join(str(m)).encode("utf8")).hexdigest()
#print(flag)
"""
加密后的密文为:
xGJ13kkRK9QDfORQomFOf9NZs9LKVZvGqVIsVO9NOkorv
"""思路:仿射密码加密,先根据密文和明文,爆破各位置存在 flag 字符串情况下对应的 a,b 值,再解密整串密文。
EXP
import string
import hashlib
#爆破
letter=string.ascii_letters+string.digits
def encrypt(m, a, b):
c = []
for i in range(len(m)):
ch=m[i]
t=(letter.index(ch) * a + b) % 62
c.append(letter[t])
d = ''.join(c)
return d
s='xGJ13kkRK9QDfORQomFOf9NZs9LKVZvGqVIsVO9NOkorv'
for a in range(50):
for b in range(50):
Cipher = encrypt('flag', a, b)
for k in range(len(s)-3):
if Cipher==s[k:k+4]:
print(Cipher,a,b)
#11 17
#解密
a=11
b=17
def decrypt(m, a, b):
import gmpy2
c = []
for i in range(len(m)):
ch=m[i]
t=((letter.index(ch) - b) * gmpy2.invert(a,62)) % 62
c.append(letter[t])
d = ''.join(c)
return d
m=decrypt(s, a, b)
print(m)
flag = hashlib.md5("".join(str(m)).encode("utf8")).hexdigest()
print(flag)
#2b9b99caae1cc49e5b5aacbc8cc22350LINE-GENERATION-TEST
"Sorry, Tazmi, I can't hold you in my arms anymore" Who said that? flag{md5(result)}
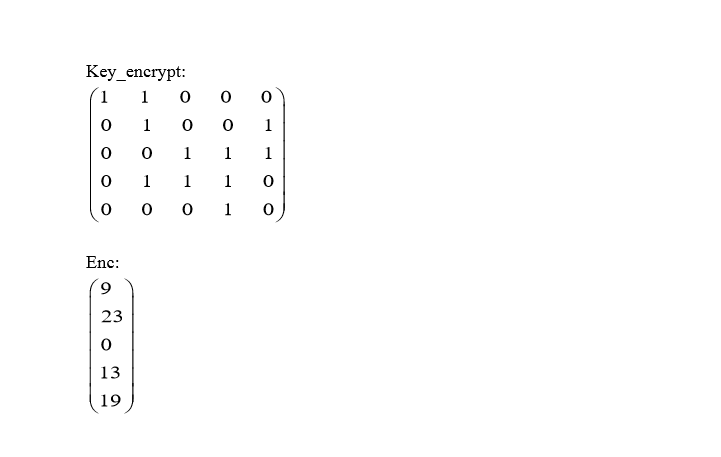
根据enc结果,猜测为 mod 26 下的矩阵运算,数值对应字母顺序,可用z3解:
EXP
from z3 import *
f=[Int(f'f{i}') for i in range(5)]
out=[9,23,0,13,19]
ss=Solver()
ss.add((f[0]+f[1])%26==out[0])
ss.add((f[1]+f[4])%26==out[1])
ss.add((f[2]+f[3]+f[4])%26==out[2])
ss.add((f[1]+f[2]+f[3])%26==out[3])
ss.add((f[3])%26==out[4])
for i in range(5):
ss.add(f[i]>=0)
ss.add(f[i]<26)
ss.check()
m=ss.model()
print(m)
res=''
for i in range(5):
res+=chr(m[f[i]].as_long()+ord('A'))
print(res)LATTICE
查看代码
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from Crypto.Util.number import *
from gmpy2 import *
flag = b'flag{******}'.strip(b'flag{').strip(b'}')
_length = len(flag)
f1, f2, f3 = [flag[_*_length//3:(_+1)*_length//3] for _ in range(3)]
e = 0x10001
# part1
m1 = bytes_to_long(f1)
p1 = getPrime(1024)
q1 = getPrime(1024)
n1 = p1 * q1
phi1 = n1 - p1 - q1 + 1
c1 = pow(m1, e, n1)
e1 = invert(getPrime(730), phi1)
e2 = invert(getPrime(730), phi1)
print(f"c1={c1}")
print(f"n1={n1}")
print(f"e1, e2={e1}, {e2}")
# c1=18256586437688071179499177390976877033843124074731118595784275706275462549393575070193713157285247155052783040660186349191946243206621283417854114947512338510120090494075462629459661733719232454448765943733550405428870484328139300079099605288398777526459160412929323065084297815106233447065396152086777361372972058145457645409788067204097788931227023450019519408351421367564315618548463098307984698849151129213729707495350390245146946120917928822783651413957541976992382340037410396051196233685887265029041398105471757470103910841819186967349443174641098166881199762042452259613391893862411694579851230262676110579543
# n1=23818305284450407798474543841442778164118430521610043726789505700531857211139233983927667740426681473611421781216471548321033175378524550659451949200683096575646597770420333524204176282763665882864564388471765969302954420394630419303362777912490426962573169221783887636684177478144311692343348905299751465406910364431823004781961449409682714094129123403882257872835302752664170847941259148324938528680748942030111986004367624657807913886922193265189704092735093802344832636336165737460259604641005316302692291726246828545907406645433265956061936110408800751546469158181520009116013316133121377819590970122050812854789
# e1, e2=9835783673095553446058291384176228043002331943350999034534623274992838739022521971236805050273046260025059987203730927700121664052723407432747645871296445872656798765584552764267628989278697521984943241908192986396530077301150942289434104385028360155639928443785704472753619847188084726935475600846835326073460115218216212785556408708462269105328394030996217916556873627266842330668453858483713498138654428487949944189108261563568558572124107380903712891578297171120862197369764331518753921684965420121318071916309204747667657476806551055584210466752436702176078704990826846481952895354353484344820523539218467328609, 17375316355314118406320219911734421029944943076411309671685926390155316380478008061756850363872585667159388923531318955662085005614917843442976105969167039475936924220396528915648168982023113542542201704319766653086540015877222620054173299245668195344488548155446059033287516207223970884670005185996184076538885012087996848877993859469631166842992572290730174768464087877396078823473042762659765399198326507762349243538341205082556290883091174177379098626493382561067493560893603313231705260729621890489619111083150474886626958850812093915647702385689897792432029133765456750687073104627271449802966450876185872407293
# part2
m2 = bytes_to_long(f2)
p2 = getPrime(1024)
q2 = getPrime(1024)
n2 = p2 * q2
phi2 = n2 - p2 - q2 + 1
c2 = pow(m2, e, n2)
e1 = invert(getPrime(818), phi2)
e2 = invert(getPrime(818), phi2)
e3 = invert(getPrime(818), phi2)
print(f"c2={c2}")
print(f"n2={n2}")
print(f"e1, e2, e3={e1}, {e2}, {e3}")
# c2=7397948118661629179431783988040895458789705611348057007436744924286606845506855024757017008422428346125155256072479048132488726422383082177040419485079781614025786874885731238970838063149169856879853922252545180431913045657720759213963468939845495598431323068663802344702417525106006065710075781595178977530059183311799912042111388947291033904817085717108188090145344450358175045073581429955014610154068361313141588492645221701328206295786968873864994686829696270486416698396375950394734029806666802284536304945414547079574607730266434796754246916153856829680842431766222116151718709429059719233175642356185763549753
# n2=26292951661012369717063123837935212187841837990937409862727543775909692635777293262933237685397758431603024805843199727419651370601525732880424359196307914374216191509283135963748357779924092043495625603225506028009487151069654694577076720362009705789203840905789543087928861357322986605749368970969266743654319969904026952962322268379225380213707065355992305857296471145718799765135536018612126827479085590220735158169406914216754985647564372724826515679007973592809045174602317195367577976810859435543162819060475161099374850589836987534136681356679103268055423382163949544464079781246652055582200248909247668623499
# e1, e2, e3=22694706397978285590465671518110674052151119930148512503108564673150680783241121101786666274181726238526861523022918702466855620573530844233715770144139721716134989018155976236479107110312927457994481310468761498848616794416315070862907683495124078074007557127579845015890427714070653740357339462879130069957999436928214586731086684031472873906400037412726424268791786559621038152550518294176306295751353922800351665127092290118894154132754742176211704948795270899801653386827500439967394284110599220882384625850203226545462281069378693815073612231125489131101884329197443266832244811697310523718069196439987874560039, 19757693768817797436014051982525313310314202171979163256271236145574495661645212918338708496186679729064506769796601795165991111866727894236670818742409747080245075024690888305402144135268609274687612318745424595896798226707126823118123835608467111180582358621936132151152853801341025288787721743741457146001947620952829255159920921457848946646082875838154605722012404441365333587571345884871498937612639283634536627265761252205175359486536891516203565325566130199281073669565197277276475101795697133209290035232673428798516588817127360784579513454813838885851841273303461997814139565597376680331988797853669080243125, 11389981852832984357137509986679549123500155102837206910639496363918096101772914255008780837117260552841880430413524483339337830003709650579991621915081444343612271861556752359650402097545780278089588646712811404815644175255214558530767310601635041857471275711027346133308388815005294337668424266111374150795611611729636047618889325059128343980592920017154112277259693587094401884519031089809597582576905458587648918184434226675368577535209126874445550629139076565822733137255015869694623787301488148409890116680369767358783472079078515354151433058595644462125347850789885910919439106962937134732744338568617745128967
# part3
m3 = bytes_to_long(f3)
nl = []
cl = []
el = []
d = getPrime(890)
for _ in range(7):
p3 = getPrime(1024)
q3 = getPrime(1024)
n3 = p3 * q3
phi3 = n3 - p3 - q3 + 1
e3 = invert(d, phi3)
c3 = pow(m3, e3, n3)
nl.append(n3)
el.append(int(e3))
cl.append(int(c3))
print(f"nl={nl}")
print(f"el={el}")
print(f"cl={cl}")
# nl=[28128431046015920275867401286356210186873411685478225083238434242778529896356941580973185976712335001794663072564844732266238921796620069046120085128987062349623903063937626930036832752240804753615027907296696919621178396785514262849051292237767466623865189316968144483530841069450843830586104632368630098173422466097902528211336564071538019195182730662473448037566051252093060016358138753900185472818830783886471271957145982784959717506947893840152372869449542083974320464199709054150465116404220039449614767664775277210885637192112937179733541728803915947236386551780231184983955344562543084441967041096292458376711, 15941506764496112508086052445327563728557019020078403891991153376527680537441120403641357307838049073871504911062932911390252596138562138738121838821774304227295619282998367749457407690200844932291746003035986895786486272990112974619702508463562341341486618806649097006148590651055205870202131969821864469531413390466032451046414385794250382725806806469557696016961113664094579447098216980438732354400216822110095599978486596626559554670623724534471803753371502013382476835636833623961163252007815503857230563136875926773677694952774930390199545373174286276659079179782760775099348228882359572989794469305007548483463, 21477075191355162812530780733492391510998687571929884007754343338217435717723078625867501718883021697292552859713102793004898230501513651427792290139803056096105899520901185500534675197066732063111553356999784006468800654532784390510131074272274140065033279545358937887893282115742876247538911953084604041666594857908821695710188977632527449792927226528437488330994788573676058689785336341090592867992073284266470554036932587257232710754132223616433438742408141296595032485887389048533539393386947037848156856122741177785829677708820778474278035795448245432257299596803757486791164446634079910181210714713733372671911, 27980889842923013696925370227314883351112276566930742332614155408917061547016052804045130934740805370672123172039414349307825814361034576591769123747969419641723024382268105732067377670209049817740440071900428023370197175270058068369286335684544707615641510484861691897469481272042885633818294183456922932916414380110239847800912427429844344314157418225375848872607078506966318368615017622795077067727056494247405810786114331212410753456354286007804891304086536769744925235306620990637998664507493246274192941211107940741079651283398114143594202874858518873967351418681842387890477536989963517627233818078769872024099, 11874512534960363610348099809383055730190731633139047777794630866338724076849679318959138590079219714369272652232029634575769480906993953424481082345379951992371000294442939639023035588875329933006584525836825284114165074336564042070288737334300716196397732835850677754402788646656939033576803885217333700571342614700068898184831574911453135933166402149352532700966385018867315597386959703124420136720323657936158849606781246207578185098868411093558545759911002127927731801893936927711562592507156698173904805443256216186768581869260553775270507875595246062147686531439308227631060321898833423587908211847300295270541, 15224675376327505356831569909735574629657890400776701610305654819907338639680897170276155541718568366576578685733979395304498350342741176913341687981341047489341678830998584508207712326879527388637351546222470352815645028747751518769571267491178143330053291625300609753897430877369550522803344790304041776136475457741607217964022820540138279326779694758410710361845223020013300516123688449750203597390967832308257425422416891725632686779454075522671608333393334956510769340136789700534379832325374383981987145894876020631335806712116055479763976321369147061003597318319341832406808540251027139169804520307379254193911, 20816310004366530476460562555539654674418948353501847467772259029157821562413984155173799071470563734631451286934848199404215819237074319460122959657265122785540839955448942096240400390688021147068313910310136849708330452368106995869836582428664254704838254068051209657594167253854071985672239873828143536953578223704832843191125646078632060809066517611352539785999159417953446228290043126014999475618992062521426364158104320015542683820261806457508236522292308223400233157038832803058231221854838414229506865129259290367651741435376247393950181576477044543309625151522964580486029253188703166701416480246712408716561]
# el=[25987918902602819707355417677858606609564539201084261601955138897744478662609433466870376126863279143678546516578590636771686005269591202142781390429352674195847557789863785630030461839151977887687779625070348014569441498317342362224053350986332682205040139621968137375627286210989585620241023030542062491956644866161789553693303924904583362137701613987159680094610425420062630506811714851881297200144117227367581461665645347500385404099699049540313824556593436186114124998427439961906526399240877190941336731287205087274899973043658083856290959261316034140784652702636341177275986111369924533651087497121981411086641, 11536583869625988508580475631817303586006854830350523024412987588935845823023883852920254639794911650478520494878968696967691629551470187064945696636487184768815655116118691937690267890433919887243265415382935382621919010979428900160889923289872309079870131039861976961857247394973842892229104187727894146945719145241398225468068442444762284423975487962972810264253002725811920750237549943221691945146164637875029949453222340170316830566866460717947954445472125958208144393628697341126850011436603502039964795983344628985478814674883393836396792128585891973468122526753412371623102847053159881215069649746044442796473, 6258382822367086007225466509089340383168990334994920939821202703275482323559910500830774564971362610273956504472668941608974102860239889022987078255597553090784741120859013739331103145046515896385914609224011705413836786407003752801490386031297804601461281831439173237022171576886020760321801450896893301134251120263729177739080455729439579694010774362517414387229006315197300961428045644005355772284786988716183767126531903718158185009941082674259385548907556563830189396453583069164801994004519642883605218373911517780829617521468589603233453056364198116633465761417250496741120018226850674916996281060732818177713, 1123271919838701598528867652197027167108863099080539439683368111052848971050356301445541307599855193093285176394529636686839284398499313003303875483280650883518085849157395654639509563320433076242436157589788737085600921802127800392348484141324778072261733029943093540242953791392717406718793264320412059241664384125317692959822942865554124478061534413794506942706216684567887262335117795180246865844961628486792518440932323761939487437693274693348212527118853647714892440036123200291042783354708238669252146887837536937057836858644441676296976517393455047925205783218624166632883408885640587672623273544610707177337, 7118479545023295405954707588228963059779204215931744790012430867010886923630125777758479840356731132074231013958169490088750850158980478630228301124508139341605160418641100871694139295433992477145251484772488467770544460756937684075318618269708022708943657701006351914547226687757500586582514797116655719921812856058421477677383120990505423968690434260247690106392926974185831928187962019940081949090884552654532497775074390863008944239582948962034595432778383883768645022793045062556784866939097597147717746406461966452475555161864364206706548330688718531837292035417777920365769331512894998241380176286709233982233, 13168734473943163973336302938913009485584587645261879444423127999237276204801622018382168698586708899788485181446147855603048194008231372985440958811912413689189104368977285091427209494304044543816972986547281293076219706872396072099247741854856260139091655620083617631378983869562381890672791152052021667510098917909814894363745294783081153365256719554496003561980502654918138082438643448784070693187085148005714372832426443057685314490413304498915962462215928873536308587910941142514653628475699545920118841784415324555829850701207604322337888161717520903549660525384083717699987039930396783965836669692586308209913, 10479961891654965767491906245342872228844927757721355813604079195987086528159311957937936581019829393661353507095655683659990579245336183813954518053160333581264563954422462161788984192939046869882345792536442687521609190445778773394934490714985370747218345404477285010857033947034316927641328406615796993324770709801331802795809891508456365006132056751453526859303222749394183497569204878882577050674415770946288236332857975211044861894002469704354986616256888238270238451220336175388799527737680012791247165508229068505716865738130520887039730007913317547732180348300974011549814044852246713637353862001647619732089]
# cl=[26990762025926015361234554701824922852211737686951071728314895652079280694833459349457539819581710501091844863357783651498529916438540415271388894954614080355176013671098789906585874283088493827368394079519107218799350991599836515587725214687726531757345836586117125798489983888025727317000884547361106409944115351385448001534261902879780968571020927393069986791941133842440263336191976813568599682529840777140658530476866114439626339887120876189411994772147548593212898680660088067972989020417831956214852302957598511086650745777023549372509081238507748441858758742568940674542745316818533509687968838045095660065593, 10187006506448325093437749195595319616438787017815805096383994457841471147784782392778196703787543049224207989504604607667426619024848476149096629397741679263594816432358822858808999754941537921535656336459441935958760974441756103850392753798600679048066631067314051766211080267819766834875185440033035269407200524143849241200928556861137591406815596425699743894432058105826025235362144103999108017137071206732151707892607679286387859478482232650312169149560302273351509494002355028010263541967524011761420957240952539252470835137718061903237470399239252503603073646645543293084875096408433482631819950804704590213310, 6437886423532401505048832011897699791749142458059174236212150075678324130837231703120523386021792518586037900591770595038410601563237211433996040367176424928889232019032175841163032057391888036430661550510359218405547004630058511178419502307233167388101271878527720260785247331379693949065587035953102280225288107902138759092336134228409786908781844325563795389688702716085105618641694958233606444462872589472346619785562576605827447340481324049463101535618702633227703494114766406229048498744719858802190984312882620049856622512923072706292686533489371133361492211391641548997776130665513185747376942409108517568769, 9109419848847714707324785769294220551699826371741022421740481799153944747138951942702248188586750915080390038722862917295761759545509031535092118635969900089921761598830510617605389891709645930785237246250062089364328837705022792423177110287540439828479475892711454759357949680768401483320330224922882420136801723810705059368507707842781543178268194075102769783446978702349789472329697747686575772335958274138755100220031340839119154414149956654777253313278877225822628523455998403052905172866471553882160286716933267892305764288184304897340982312895459694369200084691148460616870734019126068390508532732349357484737, 8351339877593066668024292626867587579118261160780795372250031046729582107846522796043372481089114437606076932490100911054500322254834811554892028468047141453946329715956923796952627591877865718723630799195025165699575257880477805590157419891041381046741986394027088622282885742946193482028755290003668399319477702639537706545291913403262719438293323658066390552307136304152762652901787194357037615440560239782969180234716552992929240295404721674843511696949057158900079758396630140897388219780133821373557024790079317123646367949487240329104202305605994129222864435721143717628545080984866553703684175979084033306658, 1964324528491408960940929058788452854160783870059496839692187136208084448309278604948579872491954065334369936581836562428242125848874621458839384825495758715562491677448056002866026151323350286710046602991373918873739469550035701019416028242241104986701591734668541888471299964830159333923615834397691438469107575406450368417418983160234443451155327263329737035233317986645236959480514469996246393545768714323729817706436697657717844493164954490820859371208274022136828013894747179248313389766670142628017962271590652010675201939163178721703732160625989524967212781547107236036268542401156332669855197379957220332115, 15290594258136384536690269021543178605821222755985953605899452132821317243018315945404106072716041806288147362903420336688433158484645044327418082073837905264849007099334862944581816752859147422920273814840319353668344366464979435623370261859929759383441080420575537882699234094906701470123926193900516484880255578323878876408561814025885958039357576248573127200715225321776940563297949344489237568596687199693667693747547169826521811101208665509704948300938983245076152307820653158912381008609443385839728517818010309909965072025108373110210561129455904261079964181719756671900849144940938572853269177896724549344582]考点:多组低解密指数攻击+共私钥指数攻击
Part1
2组e的低解密指数攻击:
# Sage
import gmpy2
N =
e1 =
e2 =
c =
for i in range(1000):
alpha2 = i/1000
M1 = int(gmpy2.mpz(N)**0.5)
M2 = int( gmpy2.mpz(N)**(1+alpha2) )
D = diagonal_matrix(ZZ, [N, M1, M2, 1])
B = Matrix(ZZ, [ [1, -N, 0, N**2],
[0, e1, -e1, -e1*N],
[0, 0, e2, -e2*N],
[0, 0, 0, e1*e2] ]) * D
L = B.LLL()
v = Matrix(ZZ, L[0])
x = v * B**(-1)
phi = (x[0,1]/x[0,0]*e1).floor()
try:
d = inverse_mod(65537, phi)
m = bytes.fromhex(hex(power_mod(c, d, N))[2:])
if len(m)<20:
print(m)
break
except:
pass
# b'89c63fd5-00c'Part2
3组e的低解密指数攻击:
# Sage
import gmpy2
N =
e1 =
e2 =
e3 =
c =
for i in range(1000):
alpha2 = i/1000
M1 = int(gmpy2.mpz(N)**(3./2))
M2 = int( gmpy2.mpz(N) )
M3 = int(gmpy2.mpz(N)**(3./2 + alpha2))
M4 = int( gmpy2.mpz(N)**(0.5) )
M5 = int( gmpy2.mpz(N)**(3./2 + alpha2) )
M6 = int( gmpy2.mpz(N)**(1.+alpha2) )
M7 = int( gmpy2.mpz(N)**(1.+alpha2) )
D = diagonal_matrix(ZZ, [M1, M2, M3, M4, M5, M6, M7, 1])
B = Matrix(ZZ, [ [1, -N, 0, N**2, 0, 0, 0, -N**3],
[0, e1, -e1, -e1*N, -e1, 0, e1*N, e1*N**2],
[0, 0, e2, -e2*N, 0, e2*N, 0, e2*N**2],
[0, 0, 0, e1*e2, 0, -e1*e2, -e1*e2, -e1*e2*N],
[0, 0, 0, 0, e3, -e3*N, -e3*N, e3*N**2],
[0, 0, 0, 0, 0, e1*e3, 0, -e1*e3*N],
[0, 0, 0, 0, 0, 0, e2*e3, -e2*e3*N],
[0, 0, 0, 0, 0, 0, 0, e1*e2*e3] ]) * D
L = B.LLL()
v = Matrix(ZZ, L[0])
x = v * B**(-1)
phi_ = (e1*x[0,1]/x[0,0]).floor()
try:
d = inverse_mod(65537, phi_)
m = hex(power_mod(c, d, N))[2:]
m = bytes.fromhex(hex(power_mod(c, d, N))[2:])
if len(m)<20:
print(m)
break
except:
pass
# b'f-4ae0-b369-' Part3
共私钥指数 d 攻击:
from gmpy2 import *
nl=[...]
el=[...]
cl=[...]
ind=[]
nl_s=sorted(nl)
for i in range(7):
ind.append(nl.index(nl_s[i]))
print(ind)
e=[]
n=[]
c=[]
for i in range(7):
e.append(el[ind[i]])
n.append(nl[ind[i]])
c.append(cl[ind[i]])
M=iroot(int(n[6]),int(2))[0]
a=[0]*8
a[0]=[M,e[0],e[1],e[2],e[3],e[4],e[5],e[6]]
a[1]=[0,-n[0],0,0,0,0,0,0]
a[2]=[0,0,-n[1],0,0,0,0,0]
a[3]=[0,0,0,-n[2],0,0,0,0]
a[4]=[0,0,0,0,-n[3],0,0,0]
a[5]=[0,0,0,0,0,-n[4],0,0]
a[6]=[0,0,0,0,0,0,-n[5],0]
a[7]=[0,0,0,0,0,0,0,-n[6]]
Mat = matrix(ZZ,a)
Mat_LLL=Mat.LLL()
d = abs(Mat_LLL[0][0])//M
print(d)
print(bytes.fromhex(hex(pow(c[6],int(d),int(n[6])))[2:]))
# b'5a3d94a20a2c'BABY-RSA
key
0101110100100111011011011000111010000111101000101010100100100011010111011000010010100101110110011101110110010100010111001110010011101010111011001100011011010110001010011111111110100110101010101110100110011010110101110110000110010101010000010110100110110110001110101011000011110100011011100101101101001000110010100111000111001111010101011011111110010111100101111001010000100010100001000111010011011111010011101100011101011010011010110001101110110110000110010011001101100000110000110100101010010010110101100101111101110000010011101110010101110100011101100110111111001010from Crypto.Util.number import *
def lfsr(status,mask):
out = (status << 1) & 0xffffffff
i=(status&mask)&0xffffffff
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
out^=lastbit
return (out,lastbit)
status= 1
mask = 0b10110001110010011100100010110101
num = bytes_to_long(m)
p = getPrime(1024)
q = getPrime(1024)
n = p*q
e = 65537
hp = bin(p)[2:]
c = pow(num, e, n)
print("n=",n)
print("c=",c)
f=open("key","w+",encoding='utf-8')
for i in range(568):
curnum = int(hp[i])
(status,out)=lfsr(status,mask)
f.write(str(curnum ^ out))
f.close()
'''
n= 9363543374665338283861145656340115756598328744870620756798779080826725774691364161648335378062705433999048117564356637094421930886166369832353405527855104576202658647651524758179962855692461154859961903531990172279764099199157181167775307950690492969859829926808950964120678082460448847927074487568619536568740301649988555476490206693181162301088156855926656544441682939839165455244630182978802660669255401576213941067679888164237586879364615664942234247896214195262510935345922512831632385741735810122730130366521612834556565838623708828780093323310348242654778247293430853566054703991781432542625271396246500576703
c= 3641304537029815746727163894554557322382012539953948183406308231174259571263608621970973671202001456955622458371303424750815017578104069924877881162707673935496925529412748663209884628320657034190702348924814794263041483260377960569530869386619921425415323912964305979776909598200202236912823968867485696101691879580799000240715778010424877093758489309380968229017074542588151574195295436881889313935734282141447498134543053106463951864974512375314091440713165047188590693431938599822340588934591712592995622334522799914563528630705687647950894928965913199772209825508001274120556508220248069647851360567609656517789
'''考点:p的高位泄露+LFSR
先用LFSR结果异或还原出p的高位hp:
def lfsr(status,mask):
out = (status << 1) & 0xffffffff
i=(status&mask)&0xffffffff
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
out^=lastbit
return (out,lastbit)
status= 1
mask = 0b10110001110010011100100010110101
c = list('0101110100100111011011011000111010000111101000101010100100100011010111011000010010100101110110011101110110010100010111001110010011101010111011001100011011010110001010011111111110100110101010101110100110011010110101110110000110010101010000010110100110110110001110101011000011110100011011100101101101001000110010100111000111001111010101011011111110010111100101111001010000100010100001000111010011011111010011101100011101011010011010110001101110110110000110010011001101100000110000110100101010010010110101100101111101110000010011101110010101110100011101100110111111001010')
c=[int(k) for k in c]
hp = ''
for i in range(568):
(status,out) = lfsr(status,mask)
hp += str(c[i]^out)
hp = int(hp, 2)
print(hp)
# 484896331241166236766986322307256381427323829969266475890843705533431739217993785274442520213477613786483789873490025705365184544110819157393140954140256890174240795425112但得到的hp只有568位,再根据Coppersmith恢复完整的p,需要爆破8位二进制位:
# Sage
n = 9363543374665338283861145656340115756598328744870620756798779080826725774691364161648335378062705433999048117564356637094421930886166369832353405527855104576202658647651524758179962855692461154859961903531990172279764099199157181167775307950690492969859829926808950964120678082460448847927074487568619536568740301649988555476490206693181162301088156855926656544441682939839165455244630182978802660669255401576213941067679888164237586879364615664942234247896214195262510935345922512831632385741735810122730130366521612834556565838623708828780093323310348242654778247293430853566054703991781432542625271396246500576703
hp = 484896331241166236766986322307256381427323829969266475890843705533431739217993785274442520213477613786483789873490025705365184544110819157393140954140256890174240795425112
import string
dic = string.digits + "abcdef"
for a in dic:
for b in dic:
pp = hex(hp) + a + b
#p需要用0补全到1024位
pp += '0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000'
#要加的数字与补全p时0的个数有关
pp = int(pp, 16)
p_fake = pp+0x10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
pbits = 1024
kbits = pbits-576
pbar = p_fake & (2^pbits-2^kbits)
#print("upper %d bits (of %d bits) is given" % (pbits-kbits, pbits))
PR.<x> = PolynomialRing(Zmod(n))
f = x + pbar
try:
x0 = f.small_roots(X=2^kbits, beta=0.4)[0] # find root < 2^kbits with factor >= n^0.4
print(x0 + pbar)
except:
pass
# 90225006288627020933267024425797647042965554486273674145474629022335483579168020321334177600624475358419458781387021577078957978886555066264514364951229871833611713144617155837023313756741716041993159155093522769416742461683810041045361926334946115547487234272520914249496954864904467634471167509689549908477最后解flag
p = 90225006288627020933267024425797647042965554486273674145474629022335483579168020321334177600624475358419458781387021577078957978886555066264514364951229871833611713144617155837023313756741716041993159155093522769416742461683810041045361926334946115547487234272520914249496954864904467634471167509689549908477
n = 9363543374665338283861145656340115756598328744870620756798779080826725774691364161648335378062705433999048117564356637094421930886166369832353405527855104576202658647651524758179962855692461154859961903531990172279764099199157181167775307950690492969859829926808950964120678082460448847927074487568619536568740301649988555476490206693181162301088156855926656544441682939839165455244630182978802660669255401576213941067679888164237586879364615664942234247896214195262510935345922512831632385741735810122730130366521612834556565838623708828780093323310348242654778247293430853566054703991781432542625271396246500576703
c = 3641304537029815746727163894554557322382012539953948183406308231174259571263608621970973671202001456955622458371303424750815017578104069924877881162707673935496925529412748663209884628320657034190702348924814794263041483260377960569530869386619921425415323912964305979776909598200202236912823968867485696101691879580799000240715778010424877093758489309380968229017074542588151574195295436881889313935734282141447498134543053106463951864974512375314091440713165047188590693431938599822340588934591712592995622334522799914563528630705687647950894928965913199772209825508001274120556508220248069647851360567609656517789
q = n//p
e = 0x10001
import gmpy2
f = (p-1)*(q-1)
d = gmpy2.invert(e,f)
m = pow(c,d,n)
print(bytes.fromhex(hex(m)[2:]))
# b'flag{fbbce1e3aa690ebb49039241f940ed26}'CRYPTO[HSC-2th]
EZVC
# -*- coding: utf-8 -*-
import flag
alphabet = 'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789!"#$%&\'()*+,-./:;<=>?@[\]^_`{|}~'
key = 'HSC'
assert flag.startswith('HSCSEC{')
flag_num_list = []
c = []
for item in flag:
flag_num_list.append(alphabet.find(item) + 1)
key_num = alphabet.find(key) + 1
for i in flag_num_list:
m = (i + key_num) % 94 - 1
if m == 0:
c.append("□")
c.append(alphabet[m-1:m])
print("c = {}".format(''.join(c)))
# c = GRBRDB`jg10ij2g01i,g201gi,2gi2,012igaigagi|由于每一位都是一一对应的,因此找到对应关系暴力枚举即可。
EXP
flag = 'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789!"#$%&\'()*+,-./:;<=>?@[\]^_`{|}~'
c = '□abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789!"#$%&\'()*+,-./:;<=>?@[\]^_`{|}'
big_dic = {}
for index in range(len(c)):
big_dic[c[index]] = flag[index]
cipher = 'GRBRDB`jg10ij2g01i,g201gi,2gi2,012igaigagi|'
for i in cipher:
print(big_dic[i], end='')
if __name__ == '__main__':
pass
#HSCSEC{kh21jk3h12j-h312hj-3hj3-123jhbjhbhj}Operator
查看代码
#!/bin/python3
from Crypto.Util.number import bytes_to_long, getPrime
FLAG = "*******************MASK****************"
# print(FLAG)
number1 = getPrime(512)
number2 = getPrime(1024)
print(number1)
result = FLAG * number1 % number2
print(result)
"""
Output:
11488359375916816818731868252559119400126174593041608170883818546254791846479664455120194350355087017477744828351806157930199157462913063513512421460678471
1890846045246997191702622225497063073251667816125412875121879991742654650976309481716690792328873189601779812108551290078049710826355501933349874438201643986975141068179879506727213209273645848165732801667704040761771
"""EXP
from Crypto.Util.number import long_to_bytes
n1 = 11488359375916816818731868252559119400126174593041608170883818546254791846479664455120194350355087017477744828351806157930199157462913063513512421460678471
c = 1890846045246997191702622225497063073251667816125412875121879991742654650976309481716690792328873189601779812108551290078049710826355501933349874438201643986975141068179879506727213209273645848165732801667704040761771
print(long_to_bytes(c // n1))
#flag{qMmZqWvmj70bBsCfmVLT}EZRSA
from Crypto.Util.number import *
import gmpy2
from flag import m
p = getPrime(1024)
q = getPrime(1024)
n = p * q
print('n =',n)
e = 0x10001
M = m * e * 1 * 2022 * p
c = pow(M,e,n)
print('c =',c)
# n = 16266043783454053154037197753138388613864200794483663334493856481522764684650995230938142916968470804276539967429581472897698022852787399956166067156691430593337430691851251036378709799238876668312530223697905925939542713491015517460139150765778057817475571231361809654951289718071760502692960235551663466242938669673675870151921605230499603814070711617511206013584605131901906195136038060653121164252894949526861390984185085201067988694831398388037080993820517447099157891181179389949333832439004857436617834100885739716577641892686620423154860716308518151628754780994043553863224363539879909831811888663875989774849
# c = 12716190507848578560760116589677996073721225715245215495257947887969923319693501568134141757778665747980229898129090929698368855086594836111461700857934476682700625486249555753323344759513528101651108919161794915999809784961533946922607642974500946026677116418317599095703217004064379100607278317877894742815660315660254853364776654303066021672567442581774299847661025422994141801987588151758971034155714424052693627277202951522779716696303237915400201362585413354036973117149974017434406560929491956957193491445847385625481870256240443170803497196783872213746269940877814806857222191433079944785910813364137603874411这个就很简单,M = m * e * 1 * 2022 * p, n = p * q 因此gcd(M,n) = p,有了p就好说了
EXP
from Crypto.Util.number import long_to_bytes
from gmpy2 import *
e = 0x10001
c = 12716190507848578560760116589677996073721225715245215495257947887969923319693501568134141757778665747980229898129090929698368855086594836111461700857934476682700625486249555753323344759513528101651108919161794915999809784961533946922607642974500946026677116418317599095703217004064379100607278317877894742815660315660254853364776654303066021672567442581774299847661025422994141801987588151758971034155714424052693627277202951522779716696303237915400201362585413354036973117149974017434406560929491956957193491445847385625481870256240443170803497196783872213746269940877814806857222191433079944785910813364137603874411
n = 16266043783454053154037197753138388613864200794483663334493856481522764684650995230938142916968470804276539967429581472897698022852787399956166067156691430593337430691851251036378709799238876668312530223697905925939542713491015517460139150765778057817475571231361809654951289718071760502692960235551663466242938669673675870151921605230499603814070711617511206013584605131901906195136038060653121164252894949526861390984185085201067988694831398388037080993820517447099157891181179389949333832439004857436617834100885739716577641892686620423154860716308518151628754780994043553863224363539879909831811888663875989774849
p = gmpy2.gcd(c, n)
q = n // p
phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi)
# M = m * e * 1 * 2022 * p
M = pow(c, d, n)
M //= e * 2022 * p
print(long_to_bytes(M))
#flag{3e5e2789a93a80615cc35edbff397c05}MISC[HSC-1th]
Sign-in
前往红客突击队公众号发送“HSC2019”并签到吧!
flag{HSC_W3LC0M3}DORAEMON
解压压缩包时得到提示
哆啦A梦把泡好的QR放进口袋后,用六位数字把自己放好了。你能找到它吗?六位数字密码爆破即可
376852得到图片宽高有问题修改下即可

然后PS补全上方两个角扫码得到
flag{sing1emak3r10v3m!sc}汝闻,人言否

哈哈!!!好图
010打开发现末尾有压缩包,把最后的4B 50改过来提取
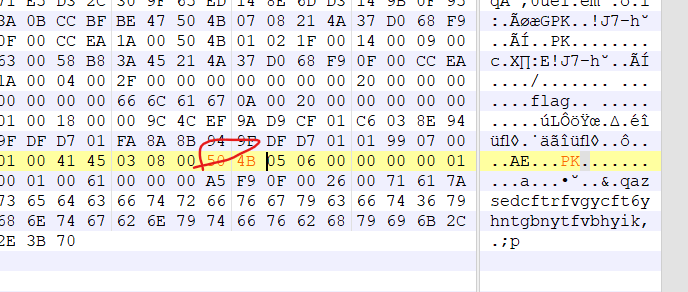
根据最后的注释得到压缩包密码:键盘密码qazsedcftrfvgycft6yhntgbnytfvbhyik,.;p,找出字母WVALOU,解压得到flag文件,010发现为wav文件结构
使用audacity查看wav文件,在频谱图发现flag:flag:e5353bb7b57578bd4da1c898a8e2d767
PERFORMANCE-ART

图片信息是两种图形替换密码的混合,其中一种为标准银河字母,猜测另一种代表数字,根据形状和出现概率,猜测出前几位 504B0304140000000,为zip压缩包文件头。
依次还原所有字符:
504b03041400000008004a7e7253148e1e
1e160000001400000006000000756e6b6e6
f778bcaadc888322ec9f30b752df70c
cfae8cca72b30400504b01021f0014000
00008004a7e7253148e1e1e16000000140
000000600240000000000000020000000000
00000756e6b6e6f770a002000000000000
1001800778284ef50dcd7016b04efef5
0dcd701e1b0ef144fdcd701504b05060
000000001000100580000003a0000000000保存为zip文件打开,得到ZmxhZ3tnNUEwIWkyZjF9base64解码得到flag{g5A0!i2f1}
WIRESHARK
010发现压缩包后有png

分离得到

zsteg发现0通道有图片
提取出来是一张二维码,扫码得到wrsak..iehr370

栅栏解码得到 wireshark3.7.0即压缩包密码
解压打开得到文件010分析发现是PDF结构,但文件头修改了,还原为25 50 44 46打开
发现是PDF隐写,使用wbStego工具提取出flag:flag{Go0dJ0B_y0ufIndLt}
PCXP
百度网盘https://pan.baidu.com/s/12q5ULEp_RD62MwbV5eE11A
提取码:1qih
奶牛快传https://cowtransfer.com/s/b76470ddc9e04a
蓝奏云https://wwo.lanzouy.com/b030r1x4j
密码:cvi0
本题目文件PCXP1与PCXP2均需要下载!
本题文件中flag{raw_Imfig3_mLs3}属于干扰项Hint
看起来里面有个镜子,你能找到吗?
两个raw文件,分别用volatility分析。
先分析:

首先查看系统版本,然后从PCXP镜像中找到并dump出rar文件,即ffflaaagggg.rar

根据提示,从PCXP1镜像中找到并dump出mirror.rar
mirror.rar的解压密码在注释地方,解压出png之后010查看发现后半部分有多余数据反序了
提取出来,然后脚本逆序一下得到key
f = open('key.png','wb').write(open('1.png','rb').read()[::-1])
然后使用密码解压ffflaaagggg.rar得到secret.pcap,foremost分离发现两张几乎一模一样的图片,盲水印。
python3 bwmforpy3.py decode png1 png2 flag.png
flag{Wat3rMarkPtysc}
MISC[HSC-2th]
SIGNIN
关注公众号:中龙 红客突击队 发送:HSCCTF{TELLMEFLAG}获取flag!
HSCSEC{W3Ic0m3_t0_HScCtF2tH}QR
Hint1
比lsb信息隐藏量更大的算法,安全性更高
Hint2
图像是按位隐藏的,所以要按位提取像素值,如果第八位是最高的非零位,那么对于rgb通道分别提取二进制数的后4 3 5位,每8位就合成一次灰度值,全部提取完再重新排列得到真正的flag图像。 ps: 原图、真正flag的图、合成后形成的这个附件图,三者像素尺寸大小一致

给了一个二维码,我们按照提示二写脚本即可
from PIL import Image
import cv2
import itertools
img = cv2.imread("qr.png", cv2.IMREAD_UNCHANGED) [:,:,::-1]
row,col = img.shape[:2]
all_r, all_g, all_b = [],[],[]
for x, y in itertools.product(range(col), range(row)):#行优先
for i, color in enumerate(img[y,x]):
if color>>7:
if i==0:
all_r+=bin(color)[2:].zfill(8)[-4:]
elif i==1:
all_g+=bin(color)[2:].zfill(8)[-3:]
elif i==2:
all_b+=bin(color)[2:].zfill(8)[-5:]
bin_str=''.join(all_r) + ''.join(all_g) + ''.join(all_b)
img=Image.new("L",size=(1000,1000),color=255)
def gen_color():
for i in range(0,len(bin_str),8):
yield int(bin_str[i:i+8],2)
g_=gen_color()
#行优先
for x in range(1000):
for y in range(1000):
try:
img.putpixel((x,y),next(g_))
except StopIteration:
break
img.show()运行得到隐藏图片

扫码得到SFNDU0VDe1lvdV9BcmVfU29fQ29vSX0base64解码得到HSCSEC{You_Are_So_CooI}
DISK
010打开图片发现文件尾有段没有特征的文件,结合题目名猜测需要用VeraCrypt
用png作为密钥文件挂载成功后目录下找到flag
fWVmYXNudXNrb29sa3NpZHtDRVNDU0gbase64解码得到
}efasnuskoolksid{CESCSH反一下得
HSCSEC{disklooksunsafe}
EZIMG
提示:flag3未尝不可尝试Online decode。

png图片尾部有01串+反转的png

1、将反转的png还原得到flag1: HSCSEC{p3G_h
2、提取所有01串画二维码,扫出 flag2:aQR_c0de_and
3、根据提示使用PixelJihad解码:https://www.mzy0.com/ctftools/pjh/

HSCSEC{p3G_haQR_c0de_and_3nc}
Salute
1.没有文件特征?勒索者最爱。
2.某张看不清的图片?
flag2/key:xxxx_xx
可以使用python还原
010分析看到文件尾有32位的MD5串
解密得到qwer1234,还发现一段奇怪的输出猜测为xor qwer1234
得到压缩包保存下来,打开得到两张图片。

zsteg查看salute1.png发现信息。结合提示可知flag2/key:that_is这个应该就是第一张的密码,秒选steghide解码

得到HSCSEC{qwer1234that_is_c0ol}
中龙技术 | HSCSEC CRY + MISC WP的更多相关文章
- buuctf misc wp 02
buuctf misc wp 02 7.LSB 8.乌镇峰会种图 9.rar 10.qr 11.ningen 12.文件中的秘密 13.wireshark 14.镜子里面的世界 15.小明的保险箱 1 ...
- php中CURL技术模拟登陆抓取数据实战,抓取某校教务处学生成绩。
这两天有基友要php中curl抓取教务处成绩的源码,用于微信公众平台的开发.下面笔者只好忍痛割爱了.php中CURL技术模拟登陆抓取数据实战,抓取沈阳工学院教务处学生成绩. 首先,教务处登录需要验证码 ...
- 转:LoadRunner中参数化技术详解
LoadRunner中参数化技术详解 LoadRunner在录制脚本的时候,只是忠实的记录了所有从客户端发送到服务器的数据,而在进行性能测试的时候,为了更接近真实的模拟现实应用,对于某些信息需要每次提 ...
- 谈谈书本《c#物联网程序设计基础》中的技术瑕疵,如果你将要读本书,请进来看看!
今天去书店看到一本名为<c#物联网程序设计基础>的书,对物联网感兴趣的我抓起来就看,书中的项目都是上位机开发项目,较简单,如果物联网开发只是这样,看起来我做物联网开发也是绰绰有余.这边书我 ...
- 关于PHP中会话技术的知识点分享
前言:在PHP中会话技术也是特别重要的,主要应用在免登录,保存一些持久化数据等等的方面,但是后期的介绍中,我将会放弃这种技术改用redis方法来替换这种方法. (一)cookie技术(即数据缓存在客户 ...
- Delphi 中DataSnap技术网摘
Delphi2010中DataSnap技术网摘 一.为DataSnap系统服务程序添加描述 这几天一直在研究Delphi 2010的DataSnap,感觉功能真是很强大,现在足有理由证明Delphi7 ...
- 转:DDR中端接技术基本概念
DDR中端接技术基本概念 版权声明:转载请注明出处:http://blog.csdn.net/lg2lh https://blog.csdn.net/lg2lh/article/details/90 ...
- 新华三孟丹:NFV资源池实现中的技术探讨
近日,在第三届未来网络发展大会SDN/NFV技术与应用创新分论坛上,新华三解决方案部架构师孟丹女士发表了主题为<NFV资源池实现中的技术探讨>的主题演讲. 孟丹指出,新华三的NFV核心理念 ...
- Flink 实战:如何解决生产环境中的技术难题?
大数据作为未来技术的基石已成为国家基础性战略资源,挖掘数据无穷潜力,将算力推至极致是整个社会面临的挑战与难题. Apache Flink 作为业界公认为最好的流计算引擎,不仅仅局限于做流处理,而是一套 ...
- buuctf misc wp 01
buuctf misc wp 01 1.金三胖 2.二维码 3.N种方法解决 4.大白 5.基础破解 6.你竟然赶我走 1.金三胖 root@kali:~/下载/CTF题目# unzip 77edf3 ...
随机推荐
- Linux中的进程页表
是什么 进程页表是用于管理进程虚拟地址空间和物理内存之间映射关系的数据结构.它记录了进程中每个虚拟页对应的物理页的信息. 什么作用 进程使用进程页表的方式是通过虚拟地址访问内存.当进程访问一个虚拟地址 ...
- Linux基础—vmvare安装及centos7安装
Linux基础 # https://zhuanlan.zhihu.com/p/429509333 # 一 什么是操作系统 Operating System(操作系统) 简称OS Windows,Mac ...
- 写一段python下载商品图片的代码
以下是一个简单的Python代码示例,用于下载商品图片: import requests import os def download_image(url, save_path): response ...
- VScode 中golang 单元测试,解决单元测试超时timeout30s
目的:单元测试的主要目的是验证代码的每个单元(函数.方法)是否按照预期工作. 提示:解决单元测试超时30s的问题在序号4 1 准备以_test.go结尾文件和导入testing包 在命名文件时需要让文 ...
- react中常见hook的使用方式与区别
1.什么是hook?react hook是react 16.8推出的方法,能够让函数式组件像类式组件一样拥有state.ref.生命周期等属性. 2.为什么要出现hook?函数式组件是全局当中一个普通 ...
- 搭建rsyncd服务
前言 rsync常用来做文件传输和同步.本文示例中客户端通过rsync同步服务端的/home/tmp目录到本地(不是将客户端的文件同步到服务端). 环境信息 IP 系统版本 rsync版本 说明 19 ...
- Redis从入门到放弃(10):分布式锁
在分布式系统中,实现对共享资源的安全访问是一个关键问题.Redis作为一种高性能的内存数据库,提供了多种方式来实现分布式锁,以解决多个节点之间对共享资源的并发访问问题. 本文将介绍五种Redis分布式 ...
- C#应用处理传入参数 - 开源研究系列文章
今天介绍关于C#的程序传入参数的处理例子. 程序的传入参数应用比较普遍,特别是一个随操作系统启动的程序,需要设置程序启动的时候不显示主窗体,而是在后台运行,于是就有了传入参数问题,比如传入/h或者/m ...
- Shiro配置类中的各个配置项浅谈
背景: 上文中在落地实践时,对Shiro进行了相关的配置,并未对其含义作用进行详细学习,本章将进一步详解其作用含义. Shiro配置类中的各个配置项的作用: @Bean public Security ...
- 程序员视角下的API数据接口对接指南
在当今互联网时代,许多应用程序和网站都需要使用第三方的API接口来获取数据.API(Application Programming Interface)允许不同的应用程序之间进行数据交互,从而提高 ...
