SMU Summer 2024 Contest Round 1

SMU Summer 2024 Contest Round 1

Dice and Coin

题意

给个 n 面骰子和一枚硬币，初始投骰子，若骰子的值在 1 到 \(K-1\) 之间则反复投硬币，硬币为正则该值翻倍，否则为 0 ，当值为 0 输掉游戏或者大于等于 \(K\) 时赢得游戏结束，问你可以赢得游戏的概率为多少。

思路

以 1 到 n 为初始值时，因为骰子为正时其值倍增，即一定是乘以一个 \(2^x\) 后大于等于 \(K\) ，所以以该值赢得游戏的概率就是 \(\frac{1}{x}\) ,累加 n 个初始值的胜利概率后除以 n 即可。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, k;
    cin >> n >> k;

    double ans = 0.0;
    i64 res = 1;
    vector<i64> c(50);
    for (int i = 0; i <= 30; i ++) {
        c[i] = res;
        res *= 2;
    }

    for (int i = 1; i <= n; i ++) {
        for (int j = 0; j <= 30; j ++) {
            if (c[j] * i >= k) {
                ans += 1.0 / (1.0 * c[j]);
                break;
            }
        }
    }

    ans /= n;

    printf("%.10lf\n", ans);

    return 0;
}

equeue

题意

给定一个长度为 n 的序列，和一个最大操作次数 k。

有以下四种操作：

• 操作 A：在序列左侧取走一个数放入手中。
• 操作 B：在序列右侧取走一个数放入手中。
• 操作 C：将手中任意一个数放在序列左侧。
• 操作 D：将手中任意一个数放在序列右侧。

也可以选择什么都不操作。

求在若干次操作后手中留下数的最大值。

思路

因数据量小，考虑暴力，但纯暴力会超时，因此需要使用优先队列优化。枚举操作A、B的次数，多出的次数则需要视情况执行C、D操作，若我们手中有一个负数，那么放回去可以使最终的和增大，反之我们则不操作，放回去的顺序一定是从小到大，负数越小，增大越多。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, k;
    cin >> n >> k;

    vector<int> a(n + 1);
    for (int i = 1; i <= n; i ++)
        cin >> a[i];

    i64 ans = 0;
    priority_queue<int, vector<int>, greater<int>> Q;
    for (int i = 0; i <= k; i ++) {
        for (int j = 0; j + i <= k && j + i <= n; j ++) {
            for (int l = 1; l <= i; l ++)
                Q.push(a[l]);
            for (int r = n; r > n - j; r --)
                Q.push(a[r]);

            i64 res = k - i - j;
            while (Q.size() && res-- && Q.top() < 0) Q.pop();

            res = 0;
            while (Q.size()) {
                res += Q.top();
                Q.pop();
            }

            ans = max(ans, res);
        }
    }

    cout << ans << '\n';

    return 0;
}

Sequence Decomposing

题意

给 n 个数，满足 $i < j $ 并且 \(A_i < A_j\)条件的可以染成一个颜色，问最少需要多少颜色可以全染色。

思路

其实类似就是让你找出若干个递增子序列，答案就是递增子序列的数量，因此我们可以从后往前枚举当前值，将当前值放在已有的递增子序列里末尾最接近它的那个序列里，比如当前值为 5 ，现有两个递增子序列 6 7 … 和 7 8 … ，最优应该是放在 6 后面，7 留给更有可能性的，否则之后再碰到 6 就需要重新以它为终点再开一个序列，那样就不是最少了。

这里我是用一个数组只存了每个序列的末尾一个数，因为也只用到这个数，当序列里有满足要求的就放进去，替换掉最后一个，否则新建一个序列。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n;
    cin >> n;

    vector<int> a(n + 1);
    for (int i = 1; i <= n; i ++)
        cin >> a[i];

    int sum = 0;

    vector<int> c;
    for (int i = n; i > 0; i --) {
        auto t = upper_bound(c.begin(), c.end(), a[i]);
        if (t == c.end()) {
            c.push_back(a[i]);
        } else {
            *t = a[i];
        }
    }

    cout << c.size() << '\n';

    return 0;
}

Cell Distance

题意

给一个 \(n\times m\) 的矩阵，从中选出 \(k\) 个点，用 \(∑_{i=1}^{K−1}∑_{j=i+1}^K(∣x_i−x_j∣+∣y_i−y_j∣)\) 计算其贡献，问你将所有方案的贡献总和模 1e9+7 的答案。

思路

转换一下，先考虑 x 坐标的贡献(将 y 的贡献看成 0 ）。

考虑两个点间 x 坐标相差为 \(d(1 ≤ d ≤ n−1)\) 时的贡献（\(d=0\) 的时候没有贡献所以这里不考虑）。设这两个点的坐标为 \((x_1,y_1)、(x_2,y_2)\)，那么就有 \(x_1 − x_2 = d，1 ≤ x_1 ，x_2 ≤ n，1 ≤ y_1 ，y_2 ≤ m\)。

则可行的 \(x_1,x_2\) 有 \(n−d\) 对 \(\{(x_1,x_2)|(1,+1),(2,+2),⋯ ,(−,)(1,d+1),(2,d+2),⋯,(n−d,n)\}\)，\(y_1,y_2\) 各有 m 种取法。所以像这样的点对共有 \((n-d) \times m^2\) 对，每一对的贡献为 d，总的贡献就是 \(d \times (n - d) \times m^2\)。

每一个点对出现在选出的 k 个点中的方案数共有 \(_{×−2}^{−2}\) （除去这两个点之外，剩下 n×m−2 个点中，选出 k−2 个点，与这两个点组成要选出的 k 个点），那么总的贡献就是 \(d×(n−d)×m^2×C_{n×m−2}^{k−2}\)。

同理可以计算 y 坐标的贡献，得到最终答案为：

\((\sum_{d=1}^{n-1}d\times (n-d)\times m^2 +\sum_{d=1}^{m-1}d\times (m-d)\times n^2)\times C_{n \times m - 2}^{k-2}\)

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

const i64 mod = 1e9 + 7;

i64 ksm(i64 x, int y) {
    i64 res = 1;
    while (y) {
        if (y & 1) res = res * x % mod;
        x = x * x % mod;
        y >>= 1;
    }
    return res;
}

i64 C(int n, int m) {
    i64 res = 1;
    for (int i = 1; i <= m; i ++)
        res = res * (n - m + i) % mod * ksm(i, mod - 2) % mod;
    return res;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, m, k;
    cin >> n >> m >> k;

    i64 ans = 0;
    for (int d = 1; d < n; d ++)
        ans = (ans + 1ll * d * (n - d) % mod * m % mod * m) % mod;
    for (int d = 1; d < m; d ++)
        ans = (ans + 1ll * d * (m - d) % mod * n % mod * n) % mod;
    ans = ans * C(n * m - 2, k - 2) % mod;

    cout << ans << '\n';

    return 0;
}

Friendships

题意

给你 n 个点，要你构造出 k 对距离为 2 的无向连通图，不能有自环和重边，如无法构造则输出 -1。

思路

距离为 2 的两个点中间必然会经过一个点，所以当拿出一个点作为所有距离为 2 的点对的中间点时，此时这个图的距离为 2 的点对达到最大值，也就是常说的菊花图。

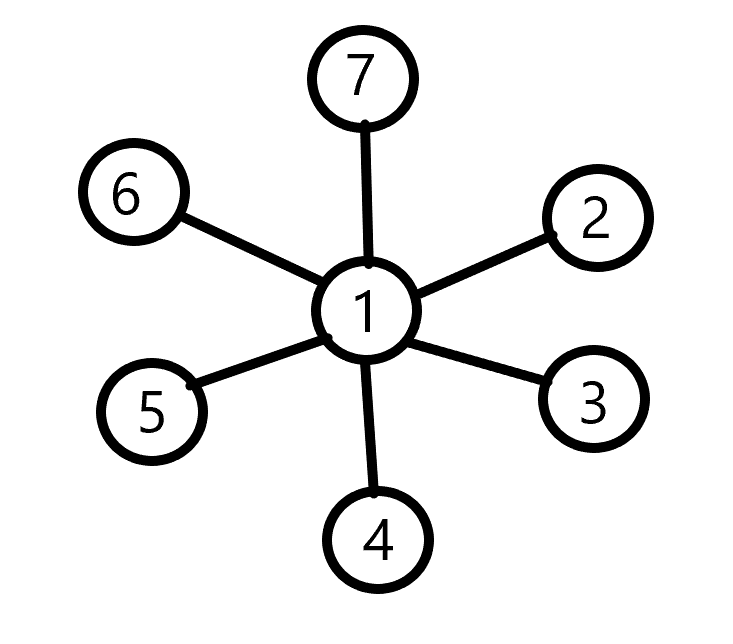
通过菊花图可以得到最多 \(m = \frac{(n-1)\times(n-2)}{2}\) 个距离为 2 的对数，这也是一个无向连通图能得到最大距离为 2 的点数，因此当 k 大于这个值时，说明不可能构造出来，小于这个值的时候我们只需要添加 \(k-m\) 条边使得这些点连成环即可。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, k;
    cin >> n >> k;

    int all = (n - 1) * (n - 2) / 2;

    if (k > all) {
        cout << "-1\n";
    } else {
        cout << n - 1 + all - k << '\n';
        for (int i = 2; i <= n; i ++)
            cout << i << " 1\n";
        for (int i = 2; i <= n; i ++)
            for (int j = i + 1; j <= n; j ++) {
                if (all == k) return 0;
                cout << i << ' ' << j << '\n';
                all --;
            }
    }

    return 0;
}

Integer Cards

题意

给 n 个数和 m 次操作，每次操作给出 B、C 两个数，可以将数组中不大于 B （可以为 0 ）个数修改成 C 的值，问最后这个 n 个数的和最大为多少。

思路

考虑离线做法，先将这 m 次操作处理出来，然后排序，这里因为map里自动排序了所以直接存进 bc 数组了，然后就是从 c 值大的往小的枚举，每次直接用一个multiset 处理可以被替换掉的数字即可，因为是从大到小的处理，所以复杂度不会有 \(O(n^2)\)。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, m;
    cin >> n >> m;

    multiset<int> s;
    vector<i64> a(n + 1);
    for (int i = 1; i <= n; i ++) {
        cin >> a[i];
        s.insert(a[i]);
    }

    vector<array<int, 2>> bc;
    map<int, int> mp;
    for (int i = 0; i < m; i ++) {
        int b, c;
        cin >> b >> c;
        mp[c] += b;
    }

    for (auto &[c, b] : mp) {
        bc.push_back({c, b});
    }

    for (int i = bc.size() - 1; i >= 0; i --) {
        auto [c, b] = bc[i];
        while (c > *s.begin() && b) {
            b --;
            s.erase(s.begin());
            s.insert(c);
        }
    }

    i64 ans = 0;
    for (auto i : s)
        ans += i;

    cout << ans << '\n';

    return 0;
}