【matlab混沌理论】1.4.双摆杆的不同参数模型
双摆杆运动模型。初始条件的微小差异,会导致千差万别的运动现象,这是混沌理论重要体现。主要考虑初始条件有两摆杆长度、质量、初始摆杆角度、重力加速度。
input:
% 参数定义
L1 = 1; % 第一根摆长
L2 = 0.5; % 第二根摆长
m1 = 1; % 第一根摆质量
m2 = 0.5; % 第二根摆质量
g = 9.81; % 重力加速度 % 初始状态定义
theta1 = pi/6; % 第一根摆角度
theta2 = 0; % 第二根摆角度
dtheta1 = 0; % 第一根摆角速度
dtheta2 = 0; % 第二根摆角速度 % 动画绘制
tspan = [0 30]; % 时间跨度
y0 = [theta1 dtheta1 theta2 dtheta2]; % 初始状态向量
[t, y] = ode45(@(t,y) pendulum2(t, y, L1, L2, m1, m2, g), tspan, y0); % 解微分方程 x1 = L1*sin(y(:,1)); % 第一根摆x坐标
y1 = -L1*cos(y(:,1)); % 第一根摆y坐标
x2 = L1*sin(y(:,1)) + L2*sin(y(:,3)); % 第二根摆x坐标
y2 = -L1*cos(y(:,1)) - L2*cos(y(:,3)); % 第二根摆y坐标 set(gcf, 'renderer', 'painters');
axis equal; % x、y轴比例相等
axis([-1.5*(L1+L2) 1.5*(L1+L2) -1.5*(L1+L2) 1.5]); % 设置坐标轴范围
hold on; x1_trace = zeros(length(t), 1); % 第一个摆的摆顶端x坐标
y1_trace = zeros(length(t), 1); % 第一个摆的摆顶端y坐标
x2_trace = zeros(length(t), 1); % 第二个摆的摆顶端x坐标
y2_trace = zeros(length(t), 1); % 第二个摆的摆顶端y坐标 % 绘制双摆动画,同时画出摆顶端轨迹连线
for k = 1:length(t)-1
plot([0 x1(k) x2(k)], [0 y1(k) y2(k)], 'linewidth', 0.5); % 绘制双摆图形
plot(x2(1:k), y2(1:k), '.', 'color', [0.8 0.05 0.1], 'markersize', 10); % 绘制尾迹
x1_trace(k+1) = L1*sin(y(k+1,1));
y1_trace(k+1) = -L1*cos(y(k+1,1));
x2_trace(k+1) = x1_trace(k+1) + L2*sin(y(k+1,3));
y2_trace(k+1) = y1_trace(k+1) - L2*cos(y(k+1,3));
plot([x1_trace(k) x1_trace(k+1)], [y1_trace(k) y1_trace(k+1)], 'linewidth', 1, 'color', 'blue'); % 第一个摆的轨迹线
plot([x2_trace(k) x2_trace(k+1)], [y2_trace(k) y2_trace(k+1)], 'linewidth', 1, 'color', 'green'); % 第二个摆的轨迹线
drawnow; % 实时显示
end % 微分方程定义
function dydt = pendulum2(t, y, L1, L2, m1, m2, g)
dydt = zeros(4,1); % 向量拆分为各个分量
theta1 = y(1);
dtheta1 = y(2);
theta2 = y(3);
dtheta2 = y(4); % 运动方程
% 第一个摆的力
F1 = -m1*L1*dtheta1^2*sin(theta1) - m1*g*cos(theta1)*sin(theta1);
% 第二个摆的力
F2 = -m2*(L1*dtheta1^2*sin(theta1) + L2*dtheta2^2*sin(theta2)) - m2*g*cos(theta2)*sin(theta2);
% 坐标加速度
d2theta1 = (F1 + m1*g*sin(theta1)*cos(theta1) + F2*cos(theta1-theta2))/(m1*L1^2 + m2*L1^2 - m2*L1*L2*cos(theta1-theta2));
d2theta2 = (F2*cos(theta1-theta2) + (m1+m2)*g*sin(theta1) + L1*dtheta1^2*sin(theta1)*cos(theta1-theta2) - (m1+m2)*L2*dtheta2^2*sin(theta1-theta2))/(L2^2*m2 + (m1+m2)*L1^2 - 2*L1*L2*m2*cos(theta1-theta2)); dydt(1) = dtheta1; % 第一个摆角速度
dydt(2) = d2theta1; % 第一个摆角加速度
dydt(3) = dtheta2; % 第二个摆角速度
dydt(4) = d2theta2; % 第二个摆角加速度
end
output:
初始条件:L1 = 1;L2 = 0.5;m1 = 1;m2 = 0.5;theta1 = pi/6;theta2 = 0;dtheta1 = 0;dtheta2 = 0;
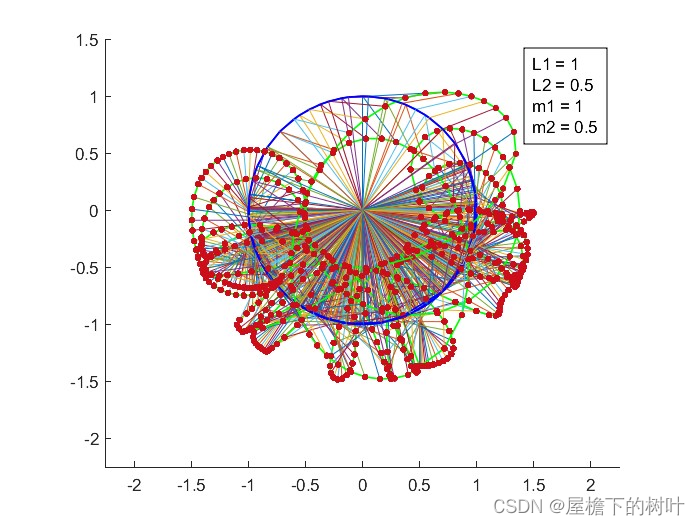
output:
初始条件:第二摆杆长度是第一摆杆的一半,其余变量也不同。
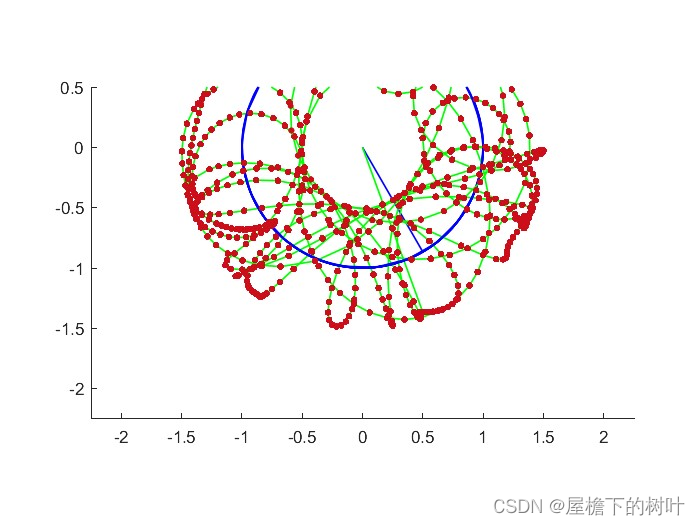
output:
初始条件:第一摆杆长度、质量等于第一摆杆的,初始摆角不同。
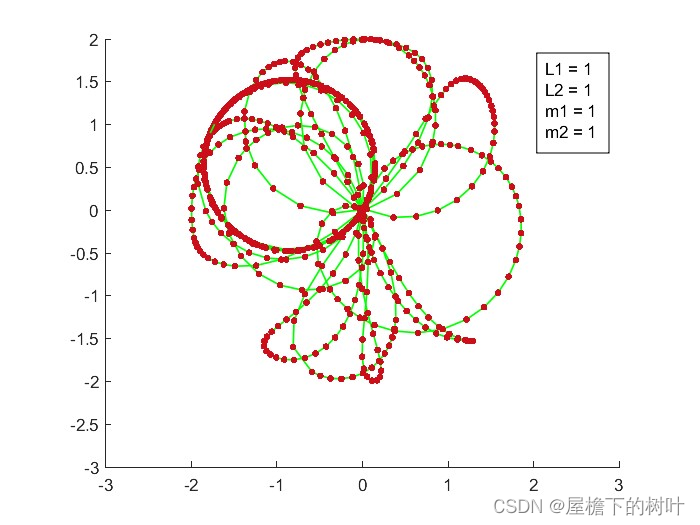
【matlab混沌理论】1.4.双摆杆的不同参数模型的更多相关文章
- 混沌理论(Chaos theory)和非线性系统
混沌理论(Chaos theory)是关于非线性系统在一定参数条件下展现分岔(bifurcation).周期运动与非周期运动相互纠缠,以至于通向某种非周期有序运动的理论.在耗散系统和保守系统中,混沌运 ...
- 如何实现Linux+Windows双系统启动
设置你的计算机根据需要启动 Windows 10 或 Ubuntu 18.04. 尽管 Linux 是一个有着广泛的硬件和软件支持的操作系统,但事实上有时你仍需要使用 Windows,也许是因为有些不 ...
- 混沌数学之Chua's circuit(蔡氏电路)
蔡氏电路(英语:Chua's circuit),一种简单的非线性电子电路设计,它可以表现出标准的混沌理论行为.在1983年,由蔡少棠教授发表,当时他正在日本早稻田大学担任访问学者[1].这个电路的制作 ...
- 《零起点,python大数据与量化交易》
<零起点,python大数据与量化交易>,这应该是国内第一部,关于python量化交易的书籍. 有出版社约稿,写本量化交易与大数据的书籍,因为好几年没写书了,再加上近期"前海智库 ...
- 【转】漫谈ANN(2):BP神经网络
上一次我们讲了M-P模型,它实际上就是对单个神经元的一种建模,还不足以模拟人脑神经系统的功能.由这些人工神经元构建出来的网络,才能够具有学习.联想.记忆和模式识别的能力.BP网络就是一种简单的人工神经 ...
- 神经网络4_BP神经网络
sklearn实战-乳腺癌细胞数据挖掘(博客主亲自录制视频教程) https://study.163.com/course/introduction.htm?courseId=1005269003&a ...
- 止损+TS
单策略单品种单策略多品种多策略单品种和加仓多策略多品种静态仓位和动态仓位 金肯特钠(kingKeltner)布林强盗(BollingerBandit)动态突破(DynamicBreakOutII)恒温 ...
- [原创]AHA大会回顾
AHA大会回顾 缘起 AHA之前参加了Daniel的培训,了解到AHA大会,觉得很高大上,开始有些心动.考虑到是工作时间,而且是外地,所以也就停留在心动层面了.之后与伯薇和四正吃饭,听说他们要去参加这 ...
- 对GBK的理解(内附全部字符编码列表):扩充的2万汉字低字节的高位不等于1,而且还剩许多编码空间没有利用
各种编码查询表:http://bm.kdd.cc/ 由于GB 2312-80只收录6763个汉字,有不少汉字,如部分在GB 2312-80推出以后才简化的汉字(如“啰”),部分人名用字(如中国前总理朱 ...
- 汉字与区位码互转(天天使用的String存储的是内码),几个常见汉字编码,附有读书笔记
汉=BABA(内码)=-A0A0=2626(区位码)字=D7D6(内码)=-A0A0=5554(区位码) 各种编码查询表:http://bm.kdd.cc/ “啊”字是GB2312之中的第一个汉字,会 ...
随机推荐
- Mac m2使用实现微信小程序抓包
Mac m2使用实现微信小程序抓包 最近换了MacBook Pro,芯片是M2 Pro,很多东西跟windows是不一样的,所以重新配置相应环境,这里介绍一下微信小程序抓包的方法. 使用burp+pr ...
- 正则表达式快速入门一:正则表达式(regex)基本语法及概念
Regex quickstart :正则表达式快速入门 author: wclsn reference quick start 如果想要了解正则表达式的基本概念且英文ok的话,完全可以从我上面所附网站 ...
- Record -「NOIP-S 2020」赛后总结
不是特别想说伤心的事情. T1 一遍过完所有大样例,此时只过去了十几二十分钟,不过之前花了半个小时通读了整个 PDF 所以此时大概过了 1h. T2 大概花了十几分钟胡出了一个反着枚举就是正解的 n^ ...
- Python 列表操作指南3
示例,将新列表中的所有值设置为 'hello': newlist = ['hello' for x in fruits] 表达式还可以包含条件,不像筛选器那样,而是作为操纵结果的一种方式: 示例,返回 ...
- Kbaor_2023_9_28_Java第一次实战项目_ELM_V1_食品的实体类、工具类与实现类
Kbaor_2023_9_28_Java第一次实战项目_ELM_V1_食品的实体类.工具类与实现类 ELM_V1_食品的实体类 package elm_V1; /** * [食品实体类] * * @a ...
- 实战0-1,Java开发者也能看懂的大模型应用开发实践!!!
前言 在前几天的文章<续写AI技术新篇,融汇工程化实践>中,我分享说在RAG领域,很多都是工程上的实践,做AI大模型应用的开发其实Java也能写,那么本文就一个Java开发者的立场,构建实 ...
- 深入解析Go非类型安全指针:技术全解与最佳实践
本文全面深入地探讨了Go非类型安全指针,特别是在Go语言环境下的应用.从基本概念.使用场景,到潜在风险和挑战,文章提供了一系列具体的代码示例和最佳实践.目的是帮助读者在保证代码安全和效率的同时,更加精 ...
- JDK 动态代理原理
代理模式 客户端不直接访问目标对象,需要通过第三者来实现间接访问对象 代理对象在客户端和目标对象之间起中介作用,能够屏蔽目标对象不想让客户端知道的内容,或增加额外的服务 动态代理 JDK 动态代理:基 ...
- js数据结构--集合
<!DOCTYPE html> <html> <head> <title></title> </head> <body&g ...
- c#组合模式详解
基础介绍: 组合模式用于表示部分-整体的层次结构.适用于希望用户忽略组合对象与单个对象的不同,用户将统一地使用组合结构中的所有对象的情况. 顾名思义,什么叫部分-整体,比如常见的前端UI,一个 ...
