OO第一单元表达式求导作业总结

第一次作业

功能描述：

对输入的表达式进行求导计算和格式正误判断

 

思路：

一开始的想法是想写一个大正则找到一个通项式，通过这个多项式来判断WRONG FORMAT，结果发现正则写的总是不完善，会漏掉一些没用考虑到的情况，所以就先写一个非法空格可能出现的所有情况的正则

　　

把带非法空格的表达式判断为WRONG FORMAT！

然后按照常数、带x的项，封装放入ArrayList动态数组中进行求导和合并，最后输出。

在处理爆栈的时候，使用了独占模式。独占与贪婪一样匹配最长。不过在独占量词模式下，正则表达式尽可能长地去匹配字符串，一旦匹配不成功就会结束匹配而不会回溯。一开始使用贪婪算法，结果输入的表达式超过1000字符后会爆栈，原因是正则表达式会尽可能长地去匹配符合规则的字符串，且会回溯。

匹配正则：

　　

　　第一次作业的结构，没有理解到继承，简单的写了三个类，Deri类里放主函数，ComputePoly把表达式的每一项抽出放进Poly类里面，

　　在Poly类里面放置系数和指数。求导完再合并同类项。

类图：

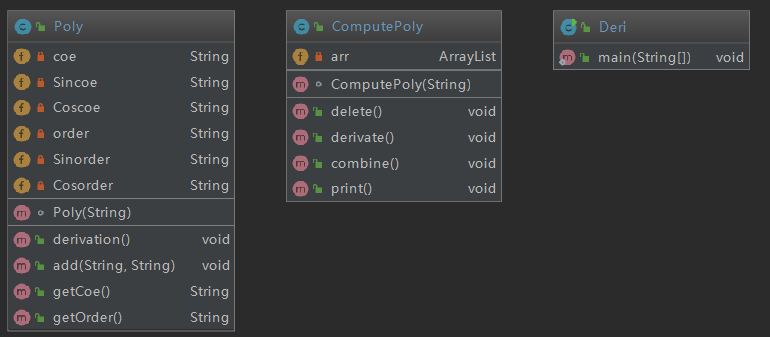
在ComputePoly类中进行了封装，传进Poly类中进行指数，系数的匹配。

BUG分析：

　　Hack:

　　　　1. 判断完系数的空格格式错误之后默认判断了x的幂的空格错误格式，就是空格格式错误的情况没有考虑全。

　　　　2. 对于空格的判断过于特殊，应该是DeBug的时候只对这一个特殊样例进行了特判，导致输出错误。

　　被Hack：

　　　　(强测与互测均未出现bug)

 

第二次作业

功能描述：

在第一次作业的基础上加入三角函数求导

思路：

延续了第一次作业的风格，在原有的基础上加上了sin(x)，cos(x)的判断和计算。

对于表达式里的每一项都可以构造一个带有系数、指数、正弦的指数、余弦的指数（每一项可以看成是常数*幂函数*正弦函数*余弦函数）

按照“*”来分割表达式作为每一项处理。

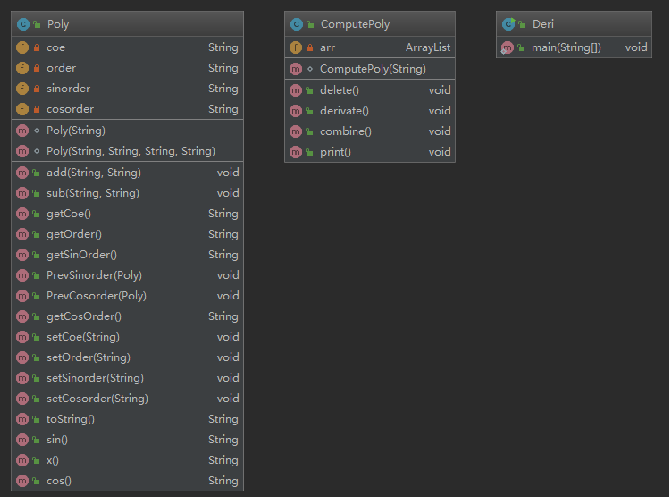
匹配正则：

　　与第一次作业相比多了三角函数的判断，不再赘述

BUG分析：

　　Hack:

　　　　1.在输出的时候错误的处理了幂为1的时候（^1），只是单纯的将”^1” replaceAll为””，

　　　　这就没有考虑幂的出现情况，导致了错误的输出。

　　　　2."/t"以及"/f"的判断过于特殊，导致格式判断出错。

　　被Hack：

　　　　在正则处理三角函数的幂时，没有构造足够多且复杂的测试集，并且因为使用大正则的原因，

　　　　并没有发现漏掉了+，导致幂只能匹配一位数 ，间接导致三角函数求导进入的判断语句错误。

第三次作业

功能描述：

对于三角函数()里可以带有常数、x的次方或者三角函数的嵌套。

思路：

改变了一下结构，用到了接口和继承，增加了一个父类，三个子类，存放不同类型的项，常数，幂函数，带三角函数

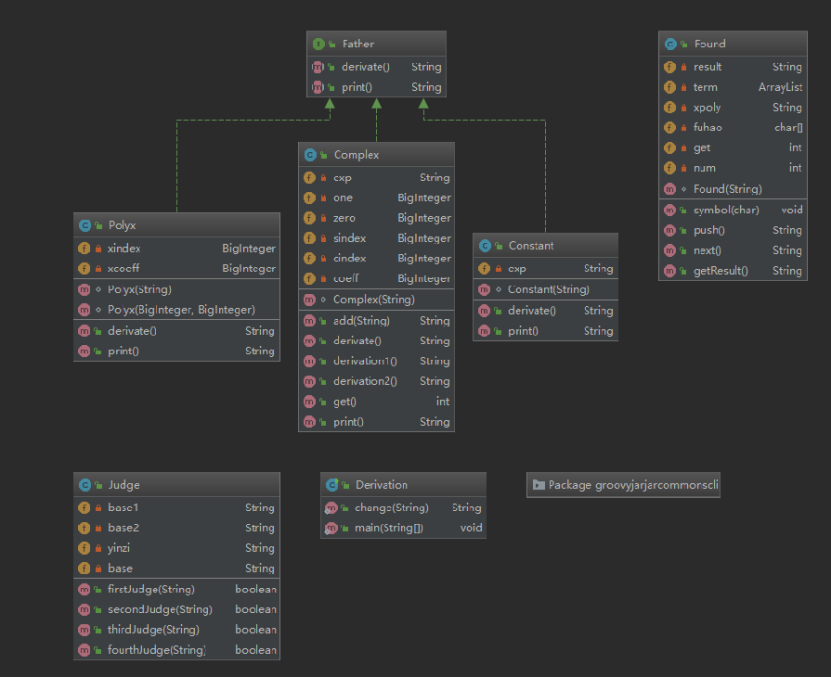
BUG分析：

　　Hack:

　　　　1. 递归处理进入死循环

　　　　2. 没有正确的处理嵌套，导致输出错误

　　　　3.括号表达格式错误

　　被Hack：

　　　　(强测与互测均未出现bug，笔者并没有进行任何性能化简)

　　 

BUG总结：

　　互测：

　　　　1.使用自己构造的测试集测试代码

　　　　2.阅读指导书，寻找边缘数据

　　　　3.阅读代码，找Bug

　　总结：

　　第一次第二次作业类与类之间并没有任何关系，第二次作业延续了第一次作业的风格，简单加入三角函数的判断即可，第三次作业用到了继承和接口，递归下降处　　 理表达式。自己的错误，在匹配表达式的正则里漏掉了+，导致只能测一位数的幂，而且我特别喜欢用大正则匹配表达式，写着写着就感觉有些情况没考虑到，就又得在正则里面修补，好在最后也没在这块摔跟头。不过研讨课的时候大佬们都推荐一种一种的匹配，还是有道理的，毕竟大正则很容易出错，检查起来还很不容易。