强化学习（八）：Eligibility Trace

Eligibility Traces

Eligibility Traces是强化学习中很基本很重要的一个概念。几乎所有的TD算法可以结合eligibility traces获得更一般化的算法，并且通常会更有效率。

Eligibility traces可以将TD和Monte Carlo算法统一起来。之前我们见过n-step方法将二者统一起来，eligibility traces 优于n-step的主要地方在于计算非常有效率，其只需要一个trace向量，而不需要储存n个特征向量。另外，eligibility trace的学习是逐步的，而不需要等到n-steps之后。

Eligibility traces机制是通过一个短期的向量得到的，这个向量称为eligibility trace $\pmb{z_t} \in R^d$。正好呼应算法中的权重向量$\pmb{w_t}\in R^d$.　大致的思想是这样的：当权重向量的某些分量参与到估计价值当中，那么与之相对应的eligibility trace分量也会立即变化，然后变化会慢慢的消失。

强化学习的很多算法都是‘向前看’的算法，即当前状态或动作的价值更新是依赖于未来状态或动作的，这样的　算法称为‘前向视角’。前向视角实施起来多少有些不方便，毕竟未来的事，当前并知道。还有另外一种思路是所谓的‘后向视角’，通过eligibility trace来考虑最近刚刚访问过的状态或动作。

The $\lambda$-return

之前定义过n-steps return为最初n rewards加上n步之后的状态的价值估计的总和：

\[G_{t:t+n} \dot = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{n-1}R_{t+n} + \gamma^n \hat v(S_{t+n}, w_{t+n-1})
\]

其实一个有效的更新不一定只依赖于n－steps return，可能依赖于多个n-step return的平均会更好，比如：

\[\frac{1}{2}G_{t:t+2} + \frac{1}{2}G_{t:t+4}
\]

$\lambda$-return 可以理解为一种特殊的平均多个n-step return，它平均所有n-step return：

\[G_{t}^{\lambda}\dot = (1- \lambda)\sum_{n=1}^{\infty}\gamma^{n-1}G_{t:t+n} = (1-\lambda)\sum_{n=1}^{T-t-1}\lambda^{n-1}G_{t:t+n} + \lambda^{T-t-1}G_{t}
\]

基于$\lambda$ return 的学习算法比如off-line $\lambda$－return algorithm:

\[w_{t+1}\dot = w_t + \alpha [ G_t^{\lambda} - \hat v(S_t, w_t)]\nabla \hat v(S_t,w_t), t = 0,..., T-1.
\]

以上其实就是一种前向视角：

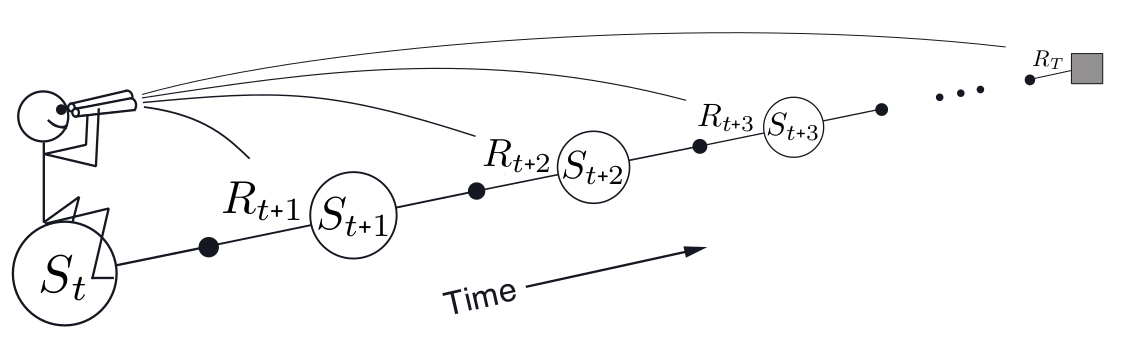
TD($\lambda$)

TD($\lambda$)是上面off-line $\lambda$-return算法的改进，主要有三点：一是它每步更新，二是因为每步更新，它的计算过程分布在每一时间步上，三是它可以应用于连续过程而不仅限于episodic problems。

如上所述，eligibility trace　通过一个向量$\pmb{z_t}\in R^d$ 实现，其与$\pmb{w_t}$维度相同，$\pmb{w_t}$可看作是长时记忆，而eligibility trace则是短时记忆。

\[z_{-1}\dot = 0, \qquad z_t\dot = \gamma \lambda z_{t-1} +\nabla\hat v(S_t,w_t),\qquad 0 \le t\le T
\]

其中$\gamma$是discount rate，$\lambda$ 是trace decay参数。Eligibility trace记录权重向量各成分在近期状态价值评估中的贡献。

TD error:

\[\delta_t \dot = R_{t+1} +\gamma\hat v(S_{t+1},w_t)- \hat v(S_t,w_t)
\]

那么权重向量的更新：

\[w_{t+1} \dot = w_t+\alpha \delta_t z_t
\]

# semi-gradient TD(lambda) for estimating v_hat = v_pi

Input: the policy pi to be evaluated

Input: a differentiable function v_hat: S_plus x R^d --> R such that v_hat(terminal,.) = 0

Algorithm parameters: step size alpha > 0, trace decay rate lambda in [0,1]

Initialize value-function weights w arbitrarily (e.g. w = 0)

Loop for each episode:

    Initialize S

    z = 0

    Loop for each step of episode:

        Choose action A based on pi(.|S)

        Take A, observe R,S'

        z = gamma * lambda *z + grad V(S,w)

        delta = R + gamma v_hat(S',w) - v_hat(S,w)

        w = w + alpha delta z

        S = S'

    until S' is terminal

TD($\lambda$)是时间上反向的，从当前状态，向后考虑已经经历过的状态。

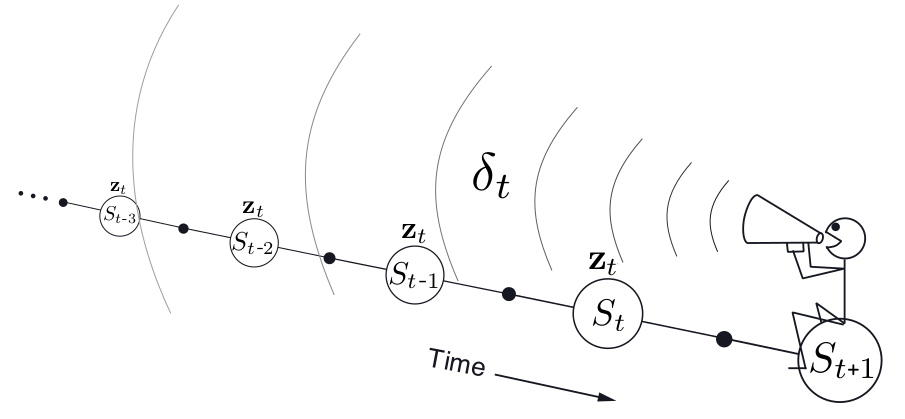
易知，当$\lambda = 0$　$TD(\lambda)$退化成为one step semi-gradient也就是TD(0)；当$　＝　１\lambda　＝　１$时，TD(1)则表现出MC的特征。

n-step Truncated $\lambda$-return Methods

线下的$\lambda-return$算法具有很大的局限性，因为$\lambda$-return要在最后才知道，在连续状态情况下，甚至永远得不到。我们知道，一般$\gamma\lambda<1$，因此太长时间的状态价值的影响就会消失掉，那么可以想到一种近似$\lambda$-return的方法称为Truncated $\lambda$-return方法：

\[G_{t:h}^{\lambda}\dot = (1-\lambda)\sum_{n =1}^{h-t-1} \lambda^{n-1}G_{t:t+n} + \lambda^{h-t-1}G_{t:h},\qquad 0 \le t<h\le T
\]

同理可以推广出truncated TD($\lambda$)(TTD($\lambda$))：

\[w_{t+n}\dot = W_{t+n-1} + \alpha [G_{t:t+n}^\lambda - \hat v(S_t,w_{t+n-1})]\nabla \hat v(S_t,w_{t+n-1})
\]

此算法可以以一种比较有效率的方式来改写，使其不依赖于n（当然，背后的理论关系还是依赖n的）：

\[G_{t:t+k}^{\lambda} = \hat v(S_t,w_{t-1}) + \sum_{i = t}^{t+k-1} (\gamma \lambda)^{i-t}\delta_i'
\]

其中$\delta_t' \dot = R_{t+1} + \gamma\hat v(S_{t+1},w_t) -\hat v(S_t,w_{t-1})$.

Redoing Updates: The On-line $\lambda$-return Algorithm

TTD($\lambda$)中n的选取是要有取舍的，n可以很大，这样更接近off-line $\lambda$-return algorithm；或者很小这样更新参数不用等很久。这两种好处增加一些计算复杂度可以都得到。

其思想是这样的：在每一步时，都会得到新的数据，然后从头重新更新。

\[w_{t+1}^h \dot = w_t^h + \alpha [G_{t:h}^h - \hat v(S_t,w_t^h)]\nabla \hat v(S_t,w_t^h),\qquad 0\le t\le h\le T.
\]

$w_t \dot = w_t^t$此即为on-line $\lambda$-return algorithm.

True On-line TD($\lambda$)

借助eligibility trace，将on-line $\lambda$ -return 的前向视角转变成后向视角即成为true on-line TD($\lambda$).

\[w_{t+1}\dot = w_t + \alpha \delta_t z_t + \alpha(w_t^Tx_t - w_{t-1}^Tx_t)(z_t - x_t)
\]

其中$\hat v(s,w) = w^T x(s),\ x_t\dot = x(S_t),\ \delta_t \dot = R_{t+1} +\gamma\hat v(S_{t+1},w_t)- \hat v(S_t,w_t),\ z_t = \dot = \gamma\lambda z_{t-1}+(1-\alpha \gamma\lambda z_{t-1}^Tx_t)x_t $.

# True On-line TD(lambda) for estimating w^T x = v_pi

Input: the policy pi to be evaluated

Input: a feature function x: S_plus --> R such that x(terminal,.) = 0

Algorithm parameters: step size alpha > 0, trace decay rate lambda in [0,1]

Initialize value-function weights w in R

Loop for each episode:

    Initialize state and obtain initial feature vector x

    z = 0

    V_old = 0

    Loop for each step of episode:

        choose A from pi.

        take action A, observe R, x'(feature vector of the next state)

        V = w^T x

        V' = w^T x'

        delta = R + gamma V' - V

        z = gamma lambda z + (1- alpha gamma z^T x)x

        w = w + alpha(delta + V- V_old)z - alpha (V-V_old) x

        V_old = V'

        x = x'

    until x' = 0(signaling arrival at a terminal state)

这里的eligibility trace 称为 dutch trace, 还有一种称为replacing trace:

\[z_{i,t} \dot =\left\{\begin{array}\\ 1\qquad if\quad x_{i,t} = 1,\\
\gamma\lambda z_{i,t-1} \qquad otherwise.\end{array}\right.
\]

Dutch Traces in Monte Carlo Learning

Eligibility traces也可应用于Monte Carlo 相产算法之中。

在梯度Monte Carlo算法的线性版本中：

\[w_{t+1} \dot = w_t +\alpha [G - w_t^Tx_t]x_t,\qquad 0 \le t \le T.
\]

其中Ｇ是在episode结束后得到的奖励，因此没有下标，也没有折扣因子。因为MC方法只能在episode结束后更新参数，这个特点我们不试图改进，而是在尽力将计算分布在各个时间步上。

\[\begin{array}\\
w_T& =& w_{T-1} + \alpha(G - w_{T-1}^Tx_{T-1})x_{T-1}\\
&=& w_{T-1} +\alpha x_{T-1}(-x_{T-1}^Tw_{T-1})+\alpha Gx_{T-1}\\
&=& (I - \alpha x_{T-1}x_{T-1}^T)w_{T-1}+\alpha Gx_{T-1}\\
&=& F_{T-1}w_{T-1}+\alpha Gx_{T-1}
\end{array}
\]

其中$F_t \dot = I - \alpha x_t x_t^T$是一个遗忘矩阵或称衰退矩阵（forgetting or fading matrix), 可以递归得到。

Ｓarsa($\lambda$)

Sarsa($\lambda$)是一个TD方法，与TD($\lambda$)类似，只不过，Sarsa($\lambda$)是针对state-action pair的：

\[w_{t+1}\dot = w_t +\alpha \delta_t z_t
\]

其中：

\[\delta \dot = R_{t+1}+\gamma \hat q(S_{t+1},A_{t+1},w_t) - \hat q(S_t,A_t,w_t)
\]

而：

\[\begin{array}\\
z_{-1} &=& 0,\\
z_t&=& \gamma \lambda z_{t-1}+\nabla\hat q(S_t,A_t,w_t),\qquad 0\le t\le T.
\end{array}
\]

# Sarsa(lambda) with binary features and linear function approximation for estimating # w^T x q_{pi} or q*

Input: a function F(s,a) returning teh set of (indices of ) active features for s,a

Input: a policy pi (if estimating q_pi)

Algorithm parameteres: step size alpha > 0, trace decay rate lambda in [0,1]

Initialize: w= (w1,...,wd)^T in R^d z = (z1,...,z_d)^T in R^d

Loop for each episode:

    Initialize S

    Choose A from pi(.|S) or e-greedy according to q_hat(S,.,w)

    z = 0

    Loop for each step of episode:

       take action A, observe R,S'

       delta =  R

       Loop for i in F(S,A):

           delta = delta - w_i

           z_i = z_i + 1  (accumulating traces)

           or z_i = 1 (replacing traces)

       If S' is terminal then:

            w = w + alpha delta z

            Go to next episode

       Choose A' in pi(.|S) or near greedily q_hat(S',.,w)

       Loop for i in F(S',A'): dleta = delta + gamma w_i

       w = w + alpha delta z

       z = gamma lambda z

       S = S', A = A'

# True Online Sarsa(lambda) for estimating w^Tx = q_pi or q*

Input: a feature function x: s_plus x A = R^d such that x(terminal,.) = 0

Input: a policy pi (if estimating q_pi)

Algorithm parameters: step size alpha >0, trace decay rate lambda in [0,1]

Initialize: w in R^d

Loop for each episode:

    Initialize S

    Choose A from pi(.|S) or nearly greedily from S using w

    x = x(S,A)

    z = 0

    Q_old = 0

    Loop for each step of episode:

        Take action A, observe R,S'

        Choose A' from pi(.|S') or near greedily from S' using w

        x' = x(S',A')

        Q = w^Tx

        Q' = w^Tx'

        delta = R + gamma Q' - Q

        z = gamma lambda z + (1 - alpha gamma lambda z^T x) x

        w = w + alpha(delta + Q - Q_old )z - alpha(Q - Q_old) x

        Q_old = Q'

        x = x'

        A = A'

    until S' is terminal

Off-policy Eligibility Traces with Control Variates

Watkins's Q($\lambda$) to Tree-Backup($\lambda$)

Stable Off-policy Methods with Traces