机器学习（九）—FP-growth算法

　　本来老师是想让我学Hadoop的，也装了Ubuntu，配置了Hadoop，一时间却不知从何学起，加之自己还是想先看点自己喜欢的算法，学习Hadoop也就暂且搁置了，不过还是想问一下园子里的朋友有什么学习Hadoop好点的资料，求推荐~言归正传，继Apriori算法之后，今天来学习FP-growth算法。

　　和Apriori算法相比，FP-growth算法只需要对数据库进行两次遍历，从而高效发现频繁项集。对于搜索引擎公司而言，他们需要通过查看互联网上的用词来找出经常在一块出现的词对，因此这些公司就需要能够高效的发现频繁项集的方法，今天要学习的FP-growth算法就可以完成此重任。

一 FP-growth算法                    

1.概述

　　FP-growth算法是基于Apriori原理的，通过将数据集存储在FP（Frequent Pattern)树上发现频繁项集，但不能发现数据之间的关联规则。FP-growth算法只需要对数据库进行两次扫描，而Apriori算法在求每个潜在的频繁项集时都需要扫描一次数据集，所以说Apriori算法是高效的。其中算法发现频繁项集的过程是：

(1)构建FP树；

(2)从FP树中挖掘频繁项集。

2. 构建FP树

　　FP表示的是频繁模式，其通过链接来连接相似元素，被连起来的元素可以看成是一个链表。将事务数据表中的各个事务对应的数据项按照支持度排序后，把每个事务中的数据项按降序依次插入到一棵以 NULL为根节点的树中，同时在每个结点处记录该结点出现的支持度。

　　FP-growth算法的流程为：首先构造FP树，然后利用它来挖掘频繁项集。在构造FP树时，需要对数据集扫描两边，第一遍扫描用来统计频率，第二遍扫描至考虑频繁项集。下面举例对FP树加以说明。

　　假设存在的一个事务数据样例为,构建FP树的步骤如下：

事务ID	事务中的元素
001	r,z,h,j,p
002	z,y,x,w,v,u,t,s
003	z
004	r,x,n,o,s
005	y,r,x,z,q,t,p
006	y,z,x,e,q,s,t,m

　　结合Apriori算法中最小支持度的阈值，在此将最小支持度定义为3，结合上表中的数据，那些不满足最小支持度要求的将不会出现在最后的FP树中，据此构建FP树，并采用一个头指针表来指向给定类型的第一个实例，快速访问FP树中的所有元素，构建的带头指针的FP树如下:

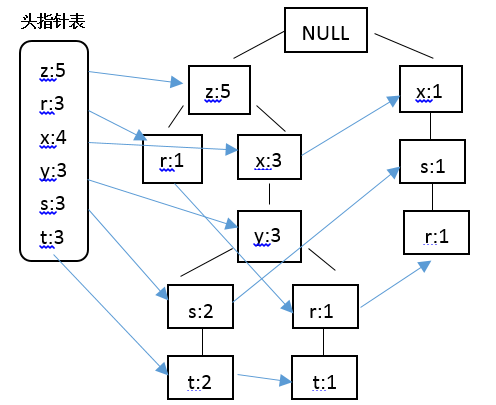
结合绘制的带头指针表的FP树，对表中数据进行过滤，排序如下：

事务ID	事务中的元素	过滤和重排序后的事务
001	r,z,h,j,p	z,r
002	z,y,x,w,v,u,t,s	z,x,y,s,t
003	z	z
004	r,x,n,o,s	x,s,r
005	y,r,x,z,q,t,p	z,x,y,r,t
006	y,z,x,e,q,s,t,m	z,x,y,s,t

在对数据项过滤排序了之后，就可以构建FP树了，从NULL开始，向其中不断添加过滤排序后的频繁项集。过程可表示为：

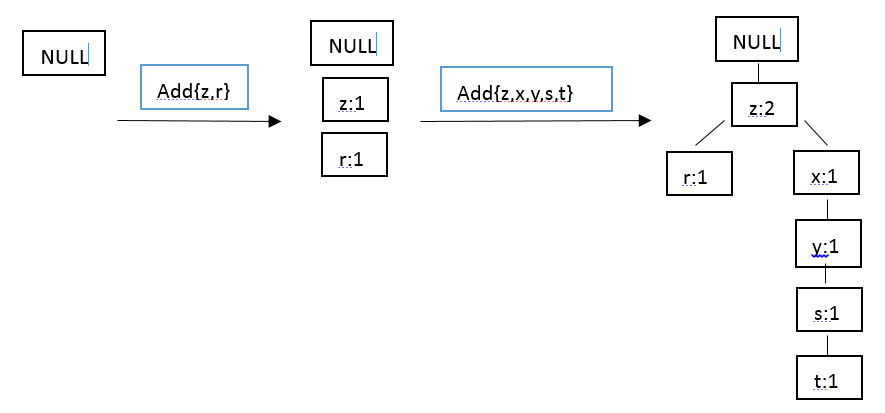
　　根据该思想就可以实现FP树的构建，下面就采用Python进行实现。我们知道，在第二次扫描数据集时会构建一棵FP树，并采用一个容器来保存树。首先创建一个类来保存树的每一个节点，代码如下：

#coding:utf-8
from numpy import *

class treeNode:
    def __init__(self, nameValue, numOccur, parentNode):
        self.name = nameValue
        self.count = numOccur
        self.nodeLink = None
        self.parent = parentNode      #needs to be updated
        self.children = {} 

    def inc(self,numOccur):
        self.count += numOccur

    def disp(self,ind = 1):
        print ' '*ind,self.name,' ',self.count
        for child in self.children.values():
            child.disp(ind+1)
'''
#test
rootNode = treeNode('pyramid',9,None)
rootNode.children['eye'] = treeNode('eye',13,None)
a = rootNode.disp()
print a
'''

这样，FP树对应的数据结构就建好了，现在就可以构建FP树了，FP树的构建函数如下:

#FP构建函数
def createTree(dataSet,minSup = 1):
    headerTable = {}
    for trans in dataSet:
        for item in trans:
            headerTable[item] = headerTable.get(item,0) + dataSet[trans]#记录每个元素项出现的频度
    for k in headerTable.keys():
        if headerTable[k] < minSup:
            del(headerTable[k])
    freqItemSet = set(headerTable.keys())
    if len(freqItemSet) == 0:#不满足最小值支持度要求的除去
        return None,None
    for k in headerTable:
        headerTable[k] = [headerTable[k],None]
    retTree = treeNode('Null Set',1,None)
    for tranSet,count in dataSet.items():
        localD = {}
        for item in tranSet:
            if item in freqItemSet:
                localD[item] = headerTable[item][0]
        if len(localD) > 0:
            orderedItems = [v[0] for v in sorted(localD.items(),key = lambda p:p[1],reverse = True)]
            updateTree(orderedItems,retTree,headerTable,count)
    return retTree,headerTable

def updateTree(items, inTree, headerTable, count):
    if items[0] in inTree.children:
        inTree.children[items[0]].inc(count)
    else:
        inTree.children[items[0]] = treeNode(items[0], count, inTree)
        if headerTable[items[0]][1] == None:
            headerTable[items[0]][1] = inTree.children[items[0]]
        else:
            updateHeader(headerTable[items[0]][1], inTree.children[items[0]])
    if len(items) > 1:
        updateTree(items[1::], inTree.children[items[0]], headerTable, count)

def updateHeader(nodeToTest, targetNode):
    while (nodeToTest.nodeLink != None):
        nodeToTest = nodeToTest.nodeLink
    nodeToTest.nodeLink = targetNode

在运行上例之前还需要一个真正的数据集，结合之前的数据自定义数据集：

def loadSimpDat():
    simpDat = [['r', 'z', 'h', 'j', 'p'],
               ['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
               ['z'],
               ['r', 'x', 'n', 'o', 's'],
               ['y', 'r', 'x', 'z', 'q', 't', 'p'],
               ['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
    return simpDat

def createInitSet(dataSet):
    retDict = {}
    for trans in dataSet:
        retDict[frozenset(trans)] = 1
    return retDict

运行：

#test
simpDat = loadSimpDat()
initSet  = createInitSet(simpDat)
myFPtree,myHeaderTab = createTree(initSet,3)
a = myFPtree.disp()
print a

这样就构建了FP树，接下来就是使用它来进行频繁项集的挖掘。

3. 从FP树中挖掘频繁项集

　　在构建了FP树之后，就可以抽取频繁项集了，这里的思想和Apriori算法大致类似，首先从氮元素项集合开始，然后在此基础上逐步构建更大的集合。大致分为三个步骤：

（1）从FP树中获得条件模式基；

（2）利用条件模式基，构建一个条件FP树；

（3）迭代重复（1）和（2），直到树包含一个元素项为止。

　　首先，获取条件模式基。条件模式基是以所查找元素项为结尾的路径集合，表示的是所查找的元素项与树根节点之间的所有内容。结合构建FP树绘制的图，r的前缀路径就是{x,s}、{z,x,y}和{z},其中的每条前缀路径都与一个计数值有关，该计数值表示的是每条路径上r的数目。为了得到这些前缀路径，结合之前所得到的头指针表，头指针表中包含相同类型元素链表的起始指针，根据每一个元素项都可以上溯到这棵树直到根节点为止。该过程对应的代码如下：

def ascendTree(leafNode, prefixPath): #ascends from leaf node to root
    if leafNode.parent != None:
        prefixPath.append(leafNode.name)
        ascendTree(leafNode.parent, prefixPath)

def findPrefixPath(basePat, treeNode): #treeNode comes from header table
    condPats = {}
    while treeNode != None:
        prefixPath = []
        ascendTree(treeNode, prefixPath)
        if len(prefixPath) > 1:
            condPats[frozenset(prefixPath[1:])] = treeNode.count
        treeNode = treeNode.nodeLink
    return condPats

#test
simpDat = loadSimpDat()
initSet  = createInitSet(simpDat)
myFPtree,myHeaderTab = createTree(initSet,3)
a = myFPtree.disp()
b = findPrefixPath('x',myHeaderTab['x'][1])
print b

　　运行代码，与所给数据一致。接下来就可以创建条件FP树了。对于每一个频繁项，都需要创建一棵条件FP树，使用刚才创建的条件模式基作为输入，采用相同的建树代码来构建树，相应的递归发现频繁项、发现条件模式基和另外的条件树。对应的递归查找频繁项集的函数如下：

def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
    bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p: p[1])]#(sort header table)
    for basePat in bigL:
        newFreqSet = preFix.copy()
        newFreqSet.add(basePat)
        freqItemList.append(newFreqSet)
        condPattBases = findPrefixPath(basePat, headerTable[basePat][1])
        myCondTree, myHead = createTree(condPattBases, minSup)
        if myHead != None:
            mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)

结合之前的数据验证发现无误。

二  从新闻网站点击流中挖掘

上述在自定义的数据中队算法进行了验证，现在选取实际的数据进行测试。在这个数据集合中，包含了100万条记录，文件中的每一行包含某个用户浏览过的新闻报道，用来寻找那些至少被10万人浏览过的报道。代码如下：

#从新闻网站点击流中挖掘
parsedData = [line.split() for line in open('kosarak.dat').readlines()]
initSet = createInitSet(parsedData)
myFPtree,myHeaderTab = createTree(initSet,100000)
myFreqList = []
a = mineTree(myFPtree,myHeaderTab,100000,set([]),myFreqList)
b = len(myFreqList)
print b
print myFreqList

这样就实现了此功能。

以上是我自己的总结和理解，难免有错，还望各位朋友不吝赐教~