NOIP 真题选讲

推荐生要凉辽

这可能是我更新的最后一篇博客

代码什么的有时间再说吧，先讲思路。(已搞定前三题代码)

首先先看一下线段覆盖题。我们有一个区间，要用线段覆盖整个区间。

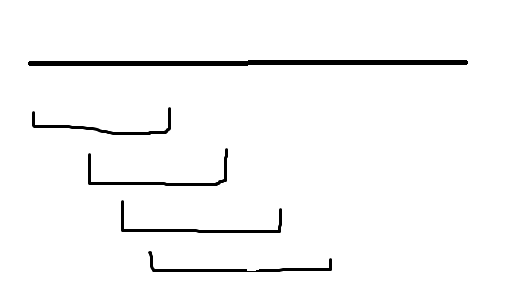
这个是线段的覆盖简图。我们如何选取最少的线段来覆盖整个区间呢？先将右端点排序，再将左端点贪心一下。

比如：

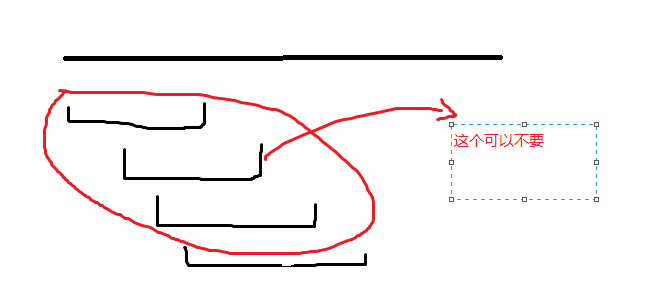
但在这个题里面覆盖的是格子，不一定连续。这就比较复杂了，我们要想点办法。我们线段覆盖解决的是格子连续的情况。所以我们要先证明第一行每个格子里的蓄水池覆盖第n行的格子是连续的。

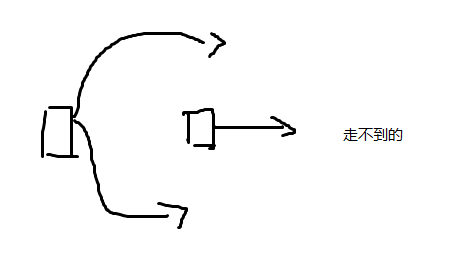
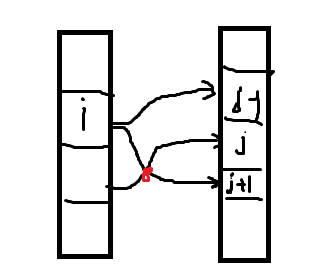
如果从i无法流到j，而能流到j-1和j+1,从别的城市可以流到j,那么这两条路线一定有一个交点,那么i也可以从这个交点流到j,这与条件矛盾。

然后这就是一个线段覆盖的问题了。因为在第1行的城市对第n行的城市覆盖的区间是连续的，就相当于在第n行进行线段盖。

我们解决能否到达时，就用dfs/bfs求一遍，顺便把第一行每个城市覆盖的第n行城市求出来，然后进行线段覆盖。

这样会T一个点，所以我们要有个优化：第一行只有比两边都搞的点才进行搜索，如果有一边比这个点高，那这个点所覆盖的区域肯定在比这个点高的子集里面。

以及注意一下n=1的情况，下面代码里会讲

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
int n,m,a[][],k,ans,ans2;
int dx[]={,-,,},dy[]={,,,-};
struct xianduan
{//处理线段
    int l, r;
    xianduan()//构造函数（结构体初始化）
    {l=2147483647;
     r=-;
    }
}xd[];//记录第一行每个点覆盖的第n行的区间
bool vis[][],vis2[];//vis记录在一次搜索中走过的点，vis2记录最后一行被覆盖的点
bool check()
{bool c=;
    for(int i=;i<=m;i++)//判断最后一行是否都被覆盖
    {
     if(!vis2[i]){c=;ans2++;}//如果有没被覆盖的，就统计个数
    }
   return c;
}
struct dl{
    int x,y;
    dl(int xx,int yy):x(xx),y(yy){}//构造函数*2
};
bool  hf(int x,int y,int xx,int yy)//广搜时判断能不能走
{
    if(xx<||yy<||xx>n||yy>m)return ;
    if(a[xx][yy]>=a[x][y])return ;
    if(vis[xx][yy])return ;
    return ;
}
queue <dl> q;
void bfs(int st)//广搜模板
{  if(a[][st]<a[][st-]||a[][st]<a[][st+])return ;
    memset(vis,,sizeof(vis));//每次搜索记得清空，不然可能会出现什么意外
    vis[][st]=;
    while(!q.empty())
    {dl ex=q.front();
     q.pop();
     for(int i=;i<;i++)
     {int xx=ex.x,yy=ex.y;
       xx+=dx[i];yy+=dy[i];
       if(hf(ex.x,ex.y,xx,yy))
       {vis[xx][yy]=;
        q.push(dl(xx,yy));
         if(xx==n)
         {if(yy>xd[st].r){xd[st].r=yy;}//记录xd[i]
          if(yy<xd[st].l){xd[st].l=yy;}
          vis2[yy]=;//因为vis每次都要清空，所以才用vis2来记录
         }
       }
     }
    }
}
int main()
{
   scanf("%d%d",&n,&m);
   for(int i=;i<=n;i++)
    for(int j=;j<=m;j++)
      scanf("%d",&a[i][j]);
   for(int i=;i<=m;i++)
      bfs(i);
  if(check())
   {int left=,r_max=;
    while(left<=m)
    {
        for(int i=;i<=m;i++)
        {if(xd[i].l<=left)r_max=max(r_max,xd[i].r);
        }
        ans++;
        left=r_max+;
    }
   printf("1\n%d\n",ans);
   }
   else
   {  if(n==)printf("1\n%d\n",ans2);//n=1时的特判。因为当n=1时，每次出队的点的vis2并不会被标记，所以没有标记的点(1,j)就是建蓄水池的点
      else printf("0\n%d\n",ans2);
   }
}

不枉我肝了近90行，wa了3次

我们先枚举第二个客栈j，找到j前面的第一个（从右往左）价格合理，颜色符合要求的客栈i。那么在i前面，颜色和i一样的客栈的数量+1就是当前j的方案数，如果在i后面，j前面还有颜色相同的客栈，那么这些客栈的方案数与j相同。

上面的式子在说些什么呢？就是当前以i为右端点的方案数，如果当前i客栈这种颜色出现的最大的地方（不包括i）k要比当前价钱合理的最大的地方t位置靠后的话，就是k的方案数。

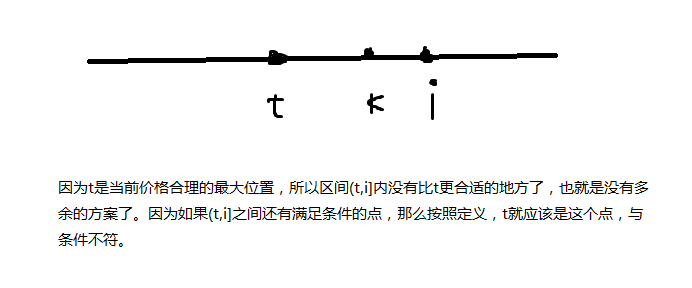
当出现这种情况时：

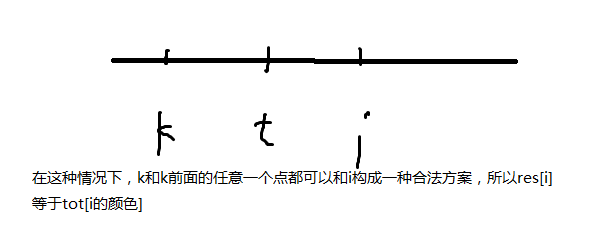
更多细节请见代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<queue>
const int MAXN=;
using namespace std;
int p,k,n,pre[MAXN],pos[],tot[],res[MAXN];
struct kezhan{
    int col,mon;//col是coler,mon是money
}a[MAXN];
int main()
{
    scanf("%d%d%d",&n,&k,&p);
    for(int i=;i<=n;i++)
     {scanf("%d%d",&a[i].col,&a[i].mon);
     if(a[i].mon<=p)pre[i]=i;//因为这里每个下标i对应的都是不一样的数，所以可以在输入中预处理
     else pre[i]=pre[i-];
     }
    for(int i=;i<=n;i++)
    {
       if(pre[i]<pos[a[i].col])//先dp,再统计tot和pos
        res[i]=res[pos[a[i].col]];
       if(pre[i]>=pos[a[i].col])
        res[i]=tot[a[i].col];
        pos[a[i].col]=i;
        tot[a[i].col]++;
    }
    long long ans=;
   for(int i=;i<=n;i++)//最后答案是每个i作为右端点的方案数的和
    ans+=res[i];
  printf("%lld",ans);
}

交了6次才A,嘤嘤嘤

首先考虑并没有加速器的情况。

设wait[i]表示到i最晚的游客到达的时刻，设arrive[i]表示车到i点的时刻。

则arrive[i]=max(arive[i-1],wait[i-1])+d[i]（d[i]就是路程）

现在我们加上加速器。

加速器可以减少距离，但并不能减少游客的到达时间,所以当游客的到达时刻大于汽车的到达时刻的时候，使用加速器就没有意义了。我们要让加速器有效，就选取arrive[i]比wait[i]大的点，进行加速，然后重复上面的过程，一直到加速器用完或是没有满足条件的边为止。

因为代码的维护不会写（树状数组优化复杂度神马的）然后翻洛谷题解，有了些新的收获。

1.这个题的维护不需要优化，因为o(n^2)也能过

2.这里贪心的是造福最多人民群众的区间（可能上课没好好听漏了点思路qwq我错惹）

代码什么的可能1个月之后才会出吧。

先理一理思路。

首先，我们预处理出车在每个点的等待时间。

递推计算每个点的arrive,并且统计在哪里会产生arrive大于wait并且用了加速器后能造福最多的人民群众，将这一段区间进行维护，一直到加速器用完为止。

维护的话，因为对一个[i,i+1]使用加速器后，可能影响到后面的arrive。如果后面的arrive>wait,就说明这里使用加速器会影响后面，否则不会。就跳出循环。

我们看到题，就会发现di的定义别扭的一批，所以我们改一下，有助于后面我们乱搞。

我们把di的定义改为从i-1到i的距离，读入就改为：

for(int i=;i<=n;i++)
 scanf("%d",&d[i]);

注意是从i=2开始读入。

我们要选择造福人数最多的点，所以我们边读入边处理到达每个点的人数。在使用加速器的时候，每次都从头开始更新造福人最多的点（注意memset(不写memset爆0警告)）,选出最多的点进行更新。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;
int goal[],d[],m,k,n,wait[],arr[],yx[],max_i,max_yx;//yx[i]是选择在i-1到i的距离-1，造福的人数，arr[i]为到达第i个点的时刻，wait[i]是每个点要等多久
struct c{
    int time,st,aim;
}ck[];
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    for(int i=;i<=n;i++)//注意i从2开始
    scanf("%d",&d[i]);
    for(int i=;i<=m;i++)
    {scanf("%d%d%d",&ck[i].time,&ck[i].st,&ck[i].aim);
     wait[ck[i].st]=max(wait[ck[i].st],ck[i].time);//处理每个点的等待时间
     goal[ck[i].aim]++;//统计每个点到达的人数
    }
    for(int i=;i<=n;i++)
      {arr[i]=max(arr[i-],wait[i-])+d[i];
      }
    while(k)//开始使用加速器
    {   max_yx=;max_i=;
       memset(yx,,sizeof(yx));//一定一定要写
        for(int i=n;i>=;i--)//倒着写递推求yx,可以减少一重循环
        {
         if(d[i]==){yx[i]=;}//如果有d被减到了0，就肯定不能再减了，所以也就不会造福人了
         else
         {if(arr[i]>wait[i])
          {yx[i]+=goal[i];
           yx[i]+=yx[i+];//这样的i可以影响到i+1
           if(yx[i+]==&&wait[i+]==)
           yx[i]+=yx[i+];//注意这里，如果某个点i+1既没有人要去，又没有人的起点是它，那么arr[i+1]一定大于wait[i+1],而且yx[i]是可以加上yx[i+2]的，所以要做特判（这个点值20分，题解里有的没有写qwq）说实话应该再来个循环判断的，但是我懒qwq
          }
          else yx[i]=goal[i];//如果无法影响到i+1,那么造福的人数就只有到达i的人
         }
        }
        for(int i=;i<=n;i++)//选最大
        {if(yx[i]>max_yx)
          {max_yx=yx[i];
           max_i=i;
          }
         }
         if(max_i==)break;
        d[max_i]--;
         k--;
        for(int i=max_i-;i<=n;i++)//简单粗暴的维护
         arr[i]=max(arr[i-],wait[i-])+d[i];
   }
    int sum=;
    for(int i=;i<=m;i++)
    {
        sum+=arr[ck[i].aim]-ck[i].time;
    }
    printf("%d\n",sum);
}

这两个人轮流来，所以在决策的时候就很麻烦，而且没有后效性。所以我们把A和B的决策算做一步。这样决策就有后效性了。

设每经过一遍决策之后到达的城市与当前所在的城市连一条边，那每个城市只有一条出边，这就是棵平衡树。dalao都说用双向链表什么的，可惜我只见过set。

我们从出发点往上跳，看能否跳到终点，当在每一层最大的边权大于x的时候就不能跳了。这里我们用树状倍增处理。

树状倍增：

设fa[i][j]表示i的第2^j个祖先。max[i][j]=max(i,fa[i][j])表示i到fa[i][j]的最大边权。二分比较。

二分答案+check。（仿佛看见当年跳石头的影子）为什么捏？你看这毒瘤数据范围，又大又圆。

怎么检查？

检查点建立的越接近首都，覆盖的路径就越多。所以我们希望检查点都建立在首都的儿子节点上。

但是有的军队可能不能在t的时间内走道首都的儿子节点，那我们不动它，把所有军队能走道的节点标记下来。每个标记的节点的子树就被控制住了。但如果还有节点没有封住，怎么办？（就像下面这样）

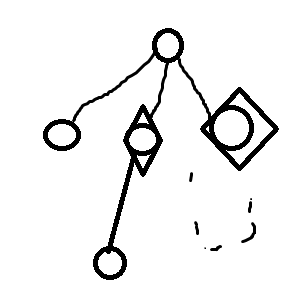
我们先假设军队在建造完成之后还可以移动。每个的剩余移动时间为d[i]，让最少的不再移动，让其他的移动到首都。再通过首都移动到没有覆盖住的点。这样我们按照剩余时间排序，看军队是否能覆盖剩余检查点。

思路：最短路。（因为最少时间啊）老师表示这玩意就是n个拼起来不想讲

暴力预处理每个状态，然后跑最短路（如果图不连通，就无解）

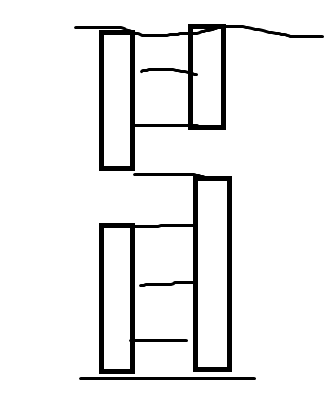
我们像上面这样把屏幕分成几个格子，看小鸟能到达哪些格子。

依旧是二分时间+判定。

二分答案后就是考虑树上两个点的距离是否小于某个数。（不加虫洞）（用树状倍增）

来我们加上虫洞。

在不加虫洞时，有些能完成，而有些完不成。要保证都能完成，我们把虫洞放在完不成的路径的交上。（选权值最大那条边）放完之后看能否都能完成。

details:

找交：看路径是否被覆盖n次。我们覆盖路径的时候，因为每次路径的次数要+1，暴力加复杂度就炸了。所以我们用前缀和的方式来整。

空间？？？真是鬼畜。（玄学）

开a[100]记录？？？

正解：设

number ,prenumber, count

if(number!=prenumber)count--;

else count++;

if(count==0)prenumber=number;

ans=prenumber;

prenumber是上一个读入的数，number是当前读入的数，重复这个玄学操作一直到最后。

这里的数据保证有解。（因为这个正解算法判不了无解，如果有毒瘤数据就裱出题人好了（小姐姐说的qwq））

首先，你建不出来补图

妈耶我又凉了

如果两个点之间没有边，那么它在补图里有边。如果有边，那在补图里就没有边。

从1开始，把和它没有边关系的点加入队列。一个一个处理队列里面的点。当队空时，就处理完了一个联通块。如果还有没有入队过的点，就从这个点开始，进行相同的操作。直到所有点都入过队。

我们考虑一下优化。用链表。