刚性方程 Stiff equation
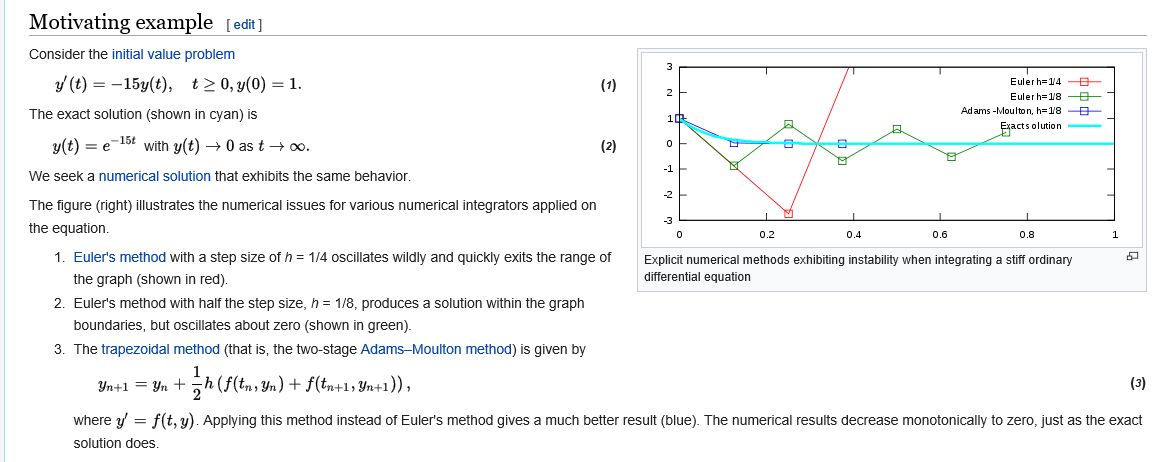
In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proven difficult to formulate a precise definition of stiffness, but the main idea is that the equation includes some terms that can lead to rapid variation in the solution.
刚性方程 Stiff equation的更多相关文章
- 方程:方程(equation)是指含有未知数的等式
方程(equation)是指含有未知数的等式.是表示两个数学式(如两个数.函数.量.运算)之间相等关系的一种等式,使等式成立的未知数的值称为“解”或“根”.求方程的解的过程称为“解方程”. 方程中文一 ...
- 吴恩达机器学习笔记13-正规方程(Normal Equation)
到目前为止,我们都在使用梯度下降算法,但是对于某些线性回归问题,正规方程方法是更好的解决方案.如: 即: 运用正规方程方法求解参数: 注:对于那些不可逆的矩阵(通常是因为特征之间不独立,如同时包含英尺 ...
- 第四讲 Yang-Mills方程与Maxwell方程
一.变分原理 变分原理始于17世纪的速降问题,也就是连接两点的曲线在有重力的情况下,让初速度为0的一小球最快地通过? 这个问题由伯努力给出解答,他的方法非常巧妙,而最后开创了一个学科——变分学.他假设 ...
- MATLAB应用专题part2-电力电子仿真技术
有匪君子,如切如磋,如琢如磨. --<诗经·卫风·淇奥> 这篇博客知识我记录一下我在仿真学习中积累到的知识和遇到的坑. 第一部分:知识部分 1.为什么电阻与电感串联电路中电流的波形比电压的 ...
- Euler-Maruyama discretization("欧拉-丸山"数值解法)
欧拉法的来源 在数学和计算机科学中,欧拉方法(Euler method)命名自它的发明者莱昂哈德·欧拉,是一种一阶数值方法,用以对给定初值的常微分方程(即初值问题)求解.它是一种解决常微分方程数值积分 ...
- Multiple View Geometry in Computer Vision Second Edition by Richard Hartley 读书笔记(一)
var bdots = "../" var sequence = [ 'l1', 'l2', 'l3', 'l4' ]; Chapter1是个总览,引出了射影几何的概念,通过在欧式 ...
- 【转】LaTeX 符号命令大全
函数.符号及特殊字符 声调 语法 效果 语法 效果 语法 效果 \bar{x} \acute{\eta} \check{\alpha} \grave{\eta} \breve{a} \ddot{y} ...
- EPnP算法
EPnP算法 相机坐标系用\(F^c\),世界坐标系用\(F^w\)表示,任何一点可以用四个控制点\(p_i^w\)表示 \begin{equation} p_i^w=\sum_{j=1}^4\alp ...
- PhysicalBasedRendering(一)物理篇
很多人对PBR的理解是存在偏差的,跳不出传统渲染模型的思维圈子,把它理解成一种模拟效果更为精确的算法公式,虽然在某种程度上是对的,但没有看到PBR的本质. PBR是对光在真实世界中与环境交互的一种近似 ...
随机推荐
- Cors 跨域 共享
CORS是一个W3C标准,全称是"跨域资源共享"(Cross-origin resource sharing). 它允许浏览器向跨源服务器,发出XMLHttpRequest请求,从 ...
- Python3的基本数据类型
2.1. Python3中六个标准的基本数据类型: Number(数字) String(字符串) Sets(集合) Tuple(元组) List(列表) Dictionary(字典) 2.2. Pyt ...
- string类find_first_not_of ()方法
string类find_first_not_of ()方法 原创作品,允许转载,转载时请务必以超链接形式标明文章 原始出处 .作者信息和本声明.否则将追究法律责任.http://xfqxj.blog. ...
- 如何创建Windows虚拟机
Windows虚拟机搭建 第1步:运行"Vmware WorkStation",看到主页面,创建新的虚拟机 第2步:新建虚拟机向导——典型(推荐) 第3步:选择光盘映像文件 第4步 ...
- html/css中BFC的开启、关闭、作用
什么是BFC BFC是什么并不重要.重要的是开启它干嘛?以及如何开启它 根据W3C的标准,在页面中元素都一个隐含的属性叫做Block Formatting Context(块级 格式化 环境)简称BF ...
- Maven-Eclipse使用maven创建HelloWorld Java项目
1.依次选择File-->New-->Other-->Maven-->Maven Project,Next 2.选择maven-archetype-quickstart,Nex ...
- 通过document.domain实现跨域访问
通过document.domain实现跨域访问:https://blog.csdn.net/nlznlz/article/details/79506655 前端跨域方法之document.domain ...
- Python学习-第二天-字符串和常用数据结构
Python学习-第二天-字符串和常用数据结构 字符串的基本操作 def main(): str1 = 'hello, world!' # 通过len函数计算字符串的长度 print(len(str1 ...
- 用Java语言做ACM的注意事项
①用Java时只需要粘贴包里面的内容,包名是不需要的.//有包名的去掉包名 ②提交题目时类名一定要是 Main,否则判题系统是不认识代码的. ③Java的util类里面的Scanner.in里面的 i ...
- html表格单元格添加斜下框线的方法
一.分隔单元格的方法 1.用“transform: rotate(-55deg);”把一条水平线旋转一定角度就成斜线了 2.利用以下命令调整分割线位置等. :after :before transfo ...
