BZOJ 1100 &&luogu 3454(计算几何+KMP）

题面

给定一个多边形，求对称轴数量。

分析

初看这似乎是一道计算几何的题目，但是如果暴力枚举对称轴，再去判断对称轴两边的边和角是否相等，时间复杂度为\(O(n^2)\),显然会TLE

问题转换

顺时针转一圈，将角和边的值连在一起就得到了一个环

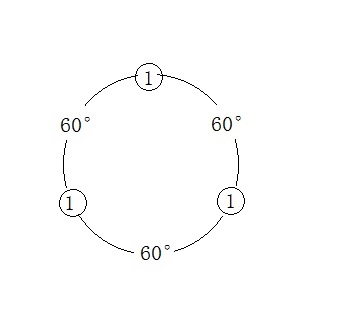
假如有一个边长为1的三角形，则它的角和边序列应该是：$ 1,60°,1,60°,1,60° $，围成一个环（角为环上的边，边为环上的结点）之后就

变成了：

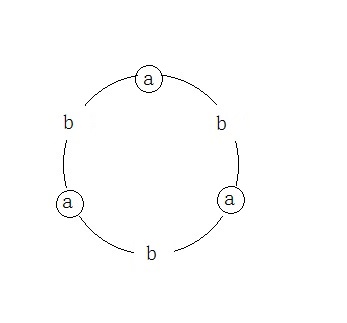
将1记为a,60°记为b，则环变为：

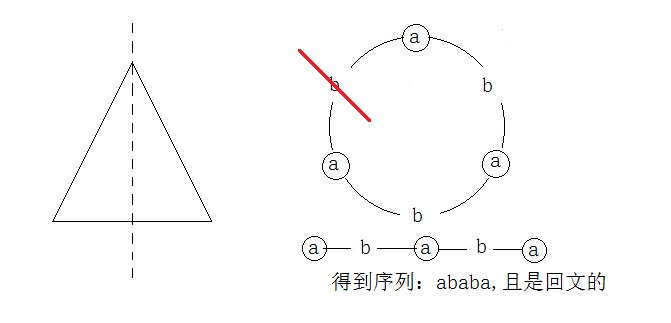
而对称轴会把这些点分成两部分，且两部分完全一样，对应到序列上就是：断开环上的某一条边，且连

成的序列是回文的

环的处理

对于环上的回文问题，我们不好处理。一种常见的处理方法是选择任意一个位置断开，将序列复制成

为2n长度的链。

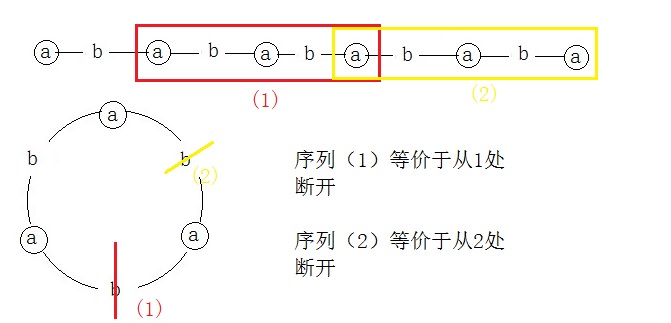
然后我们在这条链上找长度为n的回文串

找回文串

如何找回文串？Manacher算法是一种很有效的方法，但KMP的使用范围更广。先选择任意一个位置断开，记该序列为S0,再复制一遍得到序列S，将S0反过来得到串T，求S中有多少个位置和T匹配即可

时间复杂度\(O(n)\)

一些细节

• 如何处理边和角？ 边直接用长度表示（注意不必要开方，直接用长度的平方算，大量计算根号会导致TLE），而角由于考虑到图形不一定是凸多边形，采用叉积的方法记录角度，而不是点积。这里运用了叉积的性质：两向量夹角小于180°为正值，夹角大于180°为负值
• 边和角都用long long 存储，不必用double
• 序列S的长度为4n,序列T的长度为2n,数组不要开小了

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define maxn 100005
using namespace std;
inline void qread(int &x) {
	x=0;
	int sign=1;
	char c=getchar();
	while(c<'0'||c>'9') {
		if(c=='-') sign=-1;
		c=getchar();
	}
	while(c>='0'&&c<='9') {
		x=x*10+c-'0';
		c=getchar();
	}
	x=x*sign;
}

int n;
int T;
struct point {//点
	long long x;
	long long y;
	point() {

	}
	point(long long xx,long long yy) {
		x=xx;
		y=yy;
	}
	friend point operator +(point a,point b) {
		return point(a.x+b.x,a.y+b.y);
	}
	friend point operator -(point a,point b) {
		return point(a.x-b.x,a.y-b.y);
	}
} a[maxn];
typedef point vector;//在程序实现上，点和向量没有区别
long long dot(vector a,vector b) {//点积
	return a.x*b.x+a.y*b.y;
}
long long cross(vector a,vector b) {//叉积
	return a.x*b.y-a.y*b.x;
}

long long dist(point a,point b) {//计算两点间距离
	vector v=a-b;
	return dot(v,v);
}

long long work_edge(int x) {//逐一处理多边形的边，注意编号为n的点下一个点是1
	int y=x+1;
	if(y>n) y=1;
	return dist(a[x],a[y]);
}
long long work_ang(int x) {//处理角，同样注意编号为n的点下一个点是1
	int y=x+1,z=x+2;
	if(y>n) y=y%n;
	if(z>n) z=z%n;
	return cross(a[y]-a[x],a[z]-a[y]);
}
long long edge[maxn];
long long ang[maxn];
long long tmp[maxn];
int s[maxn*4];
int t[maxn*2];

int next[maxn*4];
int f[maxn*4];
int KMP(int *a,int n,int *b,int m) {//KMP模板
	next[1]=0;
	for(int i=2,j=0; i<=n; i++) {
		while(j>0&&a[i]!=a[j+1]) j=next[j];
		if(a[i]==a[j+1]) j++;
		next[i]=j;
	}
	for(int i=2,j=0; i<=m; i++) {
		while(j>0&&b[i]!=a[j+1]) j=next[j];
		if(b[i]==a[j+1]) j++;
		f[i]=j;
	}
	int cnt=0;
	for(int i=1; i<=m; i++) {
		if(f[i]==n) cnt++;
	}
	return cnt;
}
int main() {
	int x,y;
	qread(T);
	while(T--) {
		qread(n);
		for(int i=1; i<=n; i++) {
			qread(x);
			qread(y);
			a[i].x=x;
			a[i].y=y;
		}
		for(int i=1; i<=n; i++) {
			edge[i]=work_edge(i);
			ang[i]=work_ang(i);
		}
		int newn=0;
		int newm=0;
		for(int i=1; i<=n; i++) {//由于计算的角是第i与i+1条边之间的夹角，所以先加入边，再加入角
			s[++newn]=edge[i];
			s[++newn]=ang[i];
		}
		for(int i=1; i<=n; i++) {
			s[++newn]=edge[i];
			s[++newn]=ang[i];
		}
		for(int i=n*2; i>=1; i--) {
			t[++newm]=s[i];
		}
		printf("%d\n",KMP(t,newm,s,newn));
	}
}