leetcode 509斐波那契数列

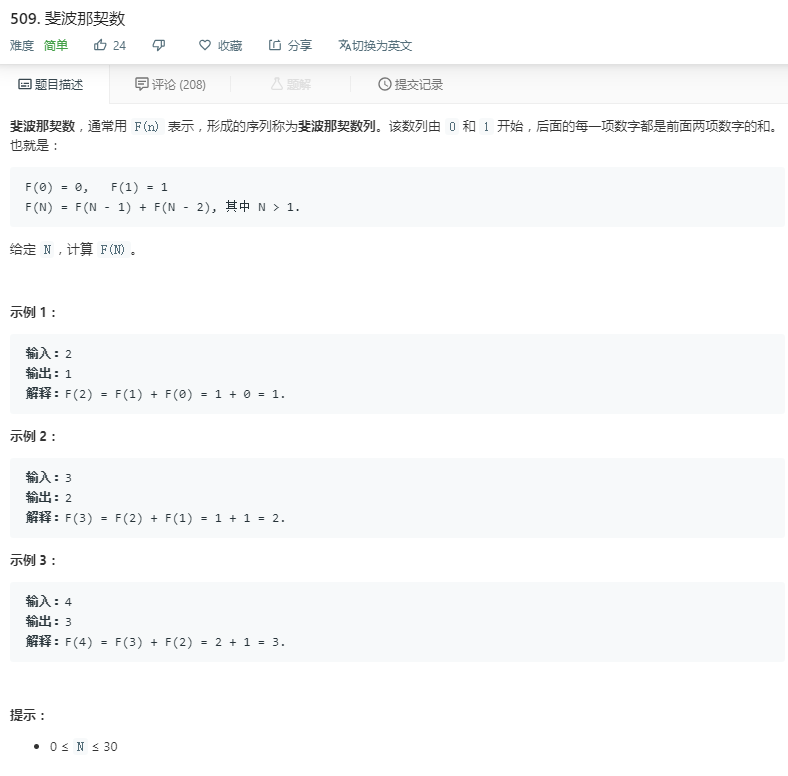
递归方法：

时间O(2^n)，空间O(logn)

class Solution {
public:
    int fib(int N) {
        return N<=?N:fib(N-)+fib(N-);
    }
};

递归+记忆化搜索：

时间O(n),空间O(logn)

class Solution {
public:
    vector<int> dp={,};

    int fib(int N) {
        if(N<=) return N;
        if(N>=dp.size()){
            int x=fib(N-)+fib(N-);
            dp.push_back(x);
        }
        return dp[N];
    }
};

动态规划：

时间O(n),空间O(n)

class Solution {
public:
    vector<int> dp={,};

    int fib(int N) {
        if(N<=) return N;
        for(int i=;i<=N;i++){
            int x=dp[i-]+dp[i-];
            dp.push_back(x);
        }
        return dp[N];
    }
};

改进版动态规划：

时间O(n),空间O(1)

class Solution {
public:
    int fib(int N) {
        if(N==) return ;
        int a=,b=;
        while(N>=){
            int tmp=b;
            b=a+b;
            a=tmp;
            N--;
        }
        return b;
    }
};

数学方法：直接通过矩阵运算算出来，参见《算法设计指南》待补充

也可参考leetcode 解答：https://leetcode-cn.com/articles/climbing-stairs/