排列perm HYSBZ - 1072（状压dp/暴力）

Description

　　给一个数字串s和正整数d, 统计s有多少种不同的排列能被d整除（可以有前导0）。例如123434有90种排列能
被2整除，其中末位为2的有30种，末位为4的有60种。

Input

　　输入第一行是一个整数T，表示测试数据的个数，以下每行一组s和d，中间用空格隔开。s保证只包含数字0, 1
, 2, 3, 4, 5, 6, 7, 8, 9.

Output

　　每个数据仅一行，表示能被d整除的排列的个数。

Sample Input

7
000 1
001 1
1234567890 1
123434 2
1234 7
12345 17
12345678 29

Sample Output

1
3
3628800
90
3
6
1398

HINT

在前三个例子中，排列分别有1, 3, 3628800种，它们都是1的倍数。

【限制】

100%的数据满足：s的长度不超过10, 1<=d<=1000, 1<=T<=15

 

 

题解

暴力可以过，但状压dp才是正解。

 

设f[s][j]表示状态s下【s表示已经选择了哪些数】余数为j的方案数，那么f[s | (1<<i-1)][(j * 10 + a[i])%d] += f[s][j]

很明显，状态s下可以通过在末尾添加一个不在状态中的i号数来转移到s|(1<<i-1)这个状态

 

设立一个状态（突然不知道怎么用语言描述这个状态）DP(I,J)，IDP(I,J)，I表示当前枚举的状态，JJ表示状态I对应的数字的数值，这样设立状态后很容易得出下面的状态转移方程： 

 

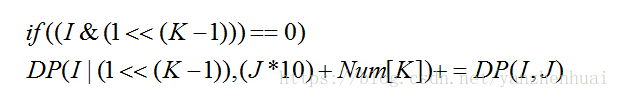
其中判断语句的含义是在II状态中，KK号没有选择出来。

状态转移结束后，由于数串中可能存在重复的数字（样例已经给出来了），这个时候我们就会有许多重复的计算。这个问题很好解决，我们根据排列的知识将最后的Ans/=Cnt[I] Cnt[I] 记录数字I在数串中出现的次数）就可以了。

C++代码/暴力

#include<bits/stdc++.h>
using namespace std;
int a[],b[];
int n ,d;
int ans ;
void dfs(int i,long long x){
    if(i > n){

        if(x % d == ) ans ++;
        return;
    }
    for(int j = ;j <= ;j ++){
        if(b[j]) {
            --b[j];
        dfs(i + ,x *  + j);
        ++b[j];
    }
    }
}

int main(){
    int t;
    cin >> t;
    while(t--){
        string str;
        cin >> str;
        ans = ;
        n = str.size();
        memset(a,,sizeof a);
        memset(b,,sizeof b);
        for(int i = ; i < str.size() ; i++){
            a[i] = str[i] - '';
            b[a[i]]++;
        }
        cin >> d;
        dfs(,);
        cout << ans << endl;
    }
}

C++代码/状压

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define DB double
#define SG string
#define LL long long
#define DP(A,B) DP[A][B]
#define Fp(A,B,C,D) for(A=B;A<=C;A+=D)
#define Fm(A,B,C,D) for(A=B;A>=C;A-=D)
#define Clear(A) memset(A,0,sizeof(A))
using namespace std;
const LL Mod=1e9+;
const LL Max=2e3+;
const LL Inf=1e18;
LL T,M,Num[Max],Cnt[Max],DP[Max][Max];
inline LL Read(){
    LL X=;char CH=getchar();bool F=;
    while(CH>''||CH<''){if(CH=='-')F=;CH=getchar();}
    while(CH>=''&&CH<=''){X=(X<<)+(X<<)+CH-'';CH=getchar();}
    return F?-X:X;
}
inline void Write(LL X){
    if(X<)X=-X,putchar('-');
    if(X>)Write(X/);
    putchar(X%+);
}
int main(){
    LL I,J,K,L;
    T=Read();
    while(T--){
        Clear(Cnt);Clear(DP);
        char CH[];scanf("%s",CH+);
        LL Length=strlen(CH+);M=Read();
        Fp(I,,Length,){
            Num[I]=CH[I]-'';
            Cnt[Num[I]]++;
        }DP(,)=;
        K=(<<Length)-;
        Fp(I,,K,){
            Fp(J,,M-,){
                Fp(L,,Length,){
                    if((I&(<<(L-)))==){
                        DP(I|(<<(L-)),((J<<)+(J<<)+Num[L])%M)+=DP(I,J);
                    }
                }
            }
        }LL Ans=DP(K,);
        Fp(I,,,){
            Fp(J,,Cnt[I],){
                Ans/=J;
            }
        }Write(Ans);putchar('\n');
    }
    return ;
}