[CodeForces - 1225E]Rock Is Push 【dp】【前缀和】

[CodeForces - 1225E]Rock Is Push 【dp】【前缀和】

标签：题解 codeforces题解 dp 前缀和

---

题目描述

Time limit

2000 ms

Memory limit

524288 kB

Source

Technocup 2020 - Elimination Round 2

Tags

binary search dp *2200

Site

https://codeforces.com/problemset/problem/1225/E

题面

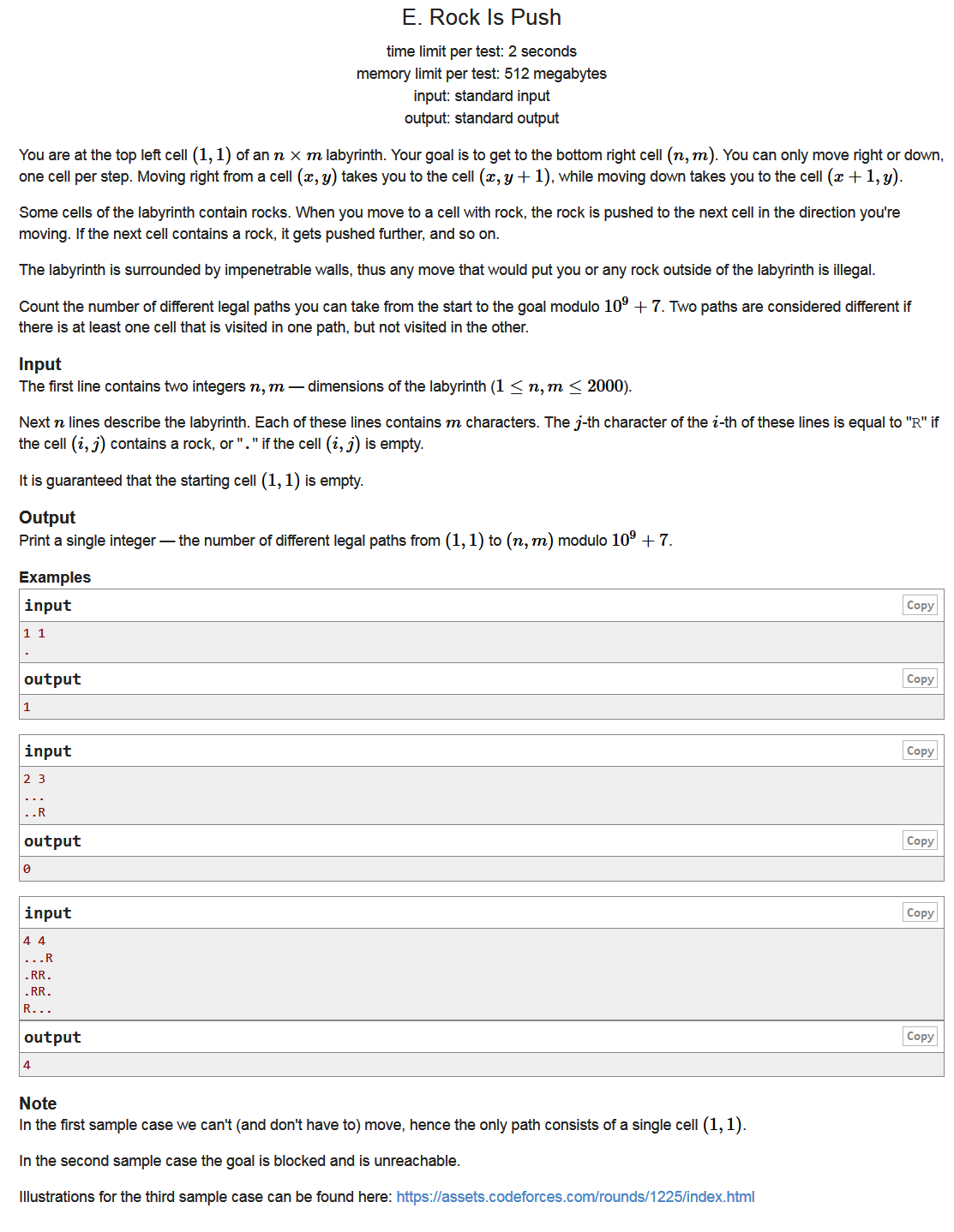
Example

Input1

1 1

.

Output1

1

Input2

2 3

...

..R

Output2

0

Input3

4 4

...R

.RR.

.RR.

R...

Output3

4

题目大意

给定\(n, m\)，和一张长宽分别为\(n,m\)的地图。\(\cdot\)代表可以通过，\(R\)代表岩石，无法通过。一个人从左上\((1,1)\)出发，想要到达右下\((n, m)\)，他每步只能向下或向右走一格。其间他可以推动与他相邻的一连串岩石一格，根据他从上一步到达这格的方向，但不能将岩石推出地图。问一共有多少条不同的走法？

例如，

\(n = 4, m = 4\)，地图为

\[\cdot \cdot \cdot R \\ \cdot R R \cdot \\ \cdot R R \cdot \\ R \cdot \cdot \cdot \\
\]

有如下四条路径，用\(PushD\)代表向下推岩石，用\(PushR\)代表向右推岩石：

1. \((1,1) \to (2,1) \to(3,1) \to PushR \to(3,2) \to(4,2) \to(4,3) \to(4,4)\)
2. \((1,1) \to(2,1)\to PushR \to(2,2)\to PushD \to(3,2)\to PushR \to(3,3)\to (4,3)\to (4,4)\)
3. \((1,1) \to(1,2)\to PushD \to(2,2)\to PushR \to(2,3)\to PushD \to(3,3)\to (3,4)\to (4,4)\)
4. \((1,1) \to(1,2)\to (1,3)\to PushD \to(2,3)\to (2,4)\to (3,4)\to (4,4)\)

---

解析

• 询问从\((1,1)\)走到\((n, m)\)的路径条数，我们也可以反过考虑从\((n, m)\)走到\((1,1)\)的路径条数。

• 我们令\(dpR[i][j]\)表示从\((i,j)\)的右边一格即从\((i, j + 1)\)到达\((i,j)\)的路径条数，令\(dpD[i][j]\)表示从\((i,j)\)的下边一格即从\((i + 1, j)\)到达\((i,j)\)的路径条数。令\(kD， kR\)分别为从\((i,j)\)到此列最下端和此行最右端的岩石总数。因为岩石可以向右推至地图边缘，所以我们易得$$dpD[i][j] = \sum_{t=i + 1}^{n - kD}dpR[t][j].$$将此列中行坐标在区间\([i+1， n-kD]\)的全部能从右边到达的路径条数都加入\(dpD[i][j]\)中。
  
  
  
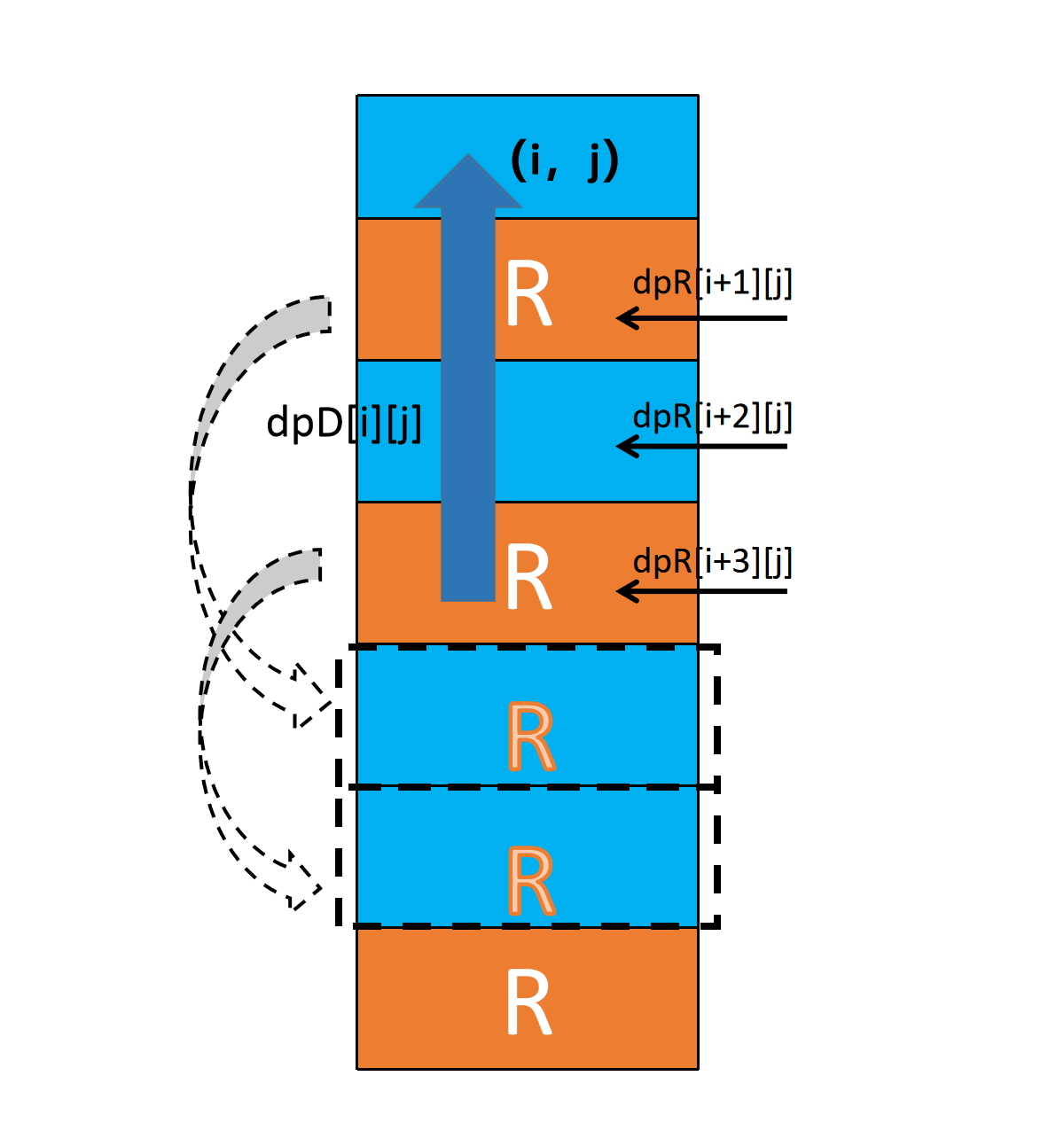
  计算\(dpD\)示意图
  
  同理，我们可得$$dpR[i][j] = \sum_{t=j + 1}^{m - kR}dpD[i][t].$$

• 为了得到每点的\(kR,kD\)，我们需要分别预处理一下每行每列从右至左，从下至上的岩石数量的前缀和。
  
  \((i,j)\)以右（包括\((i,j)\)）的全部岩石数量：\(numR[i][j] = numR[i][j + 1] + (s[i][j] == \,'R')\)；
  
  \((i,j)\)以下（包括\((i,j)\)）的全部岩石数量：\(numD[i][j] = numD[i + 1][j] + (s[i][j] == \,'R')\)。

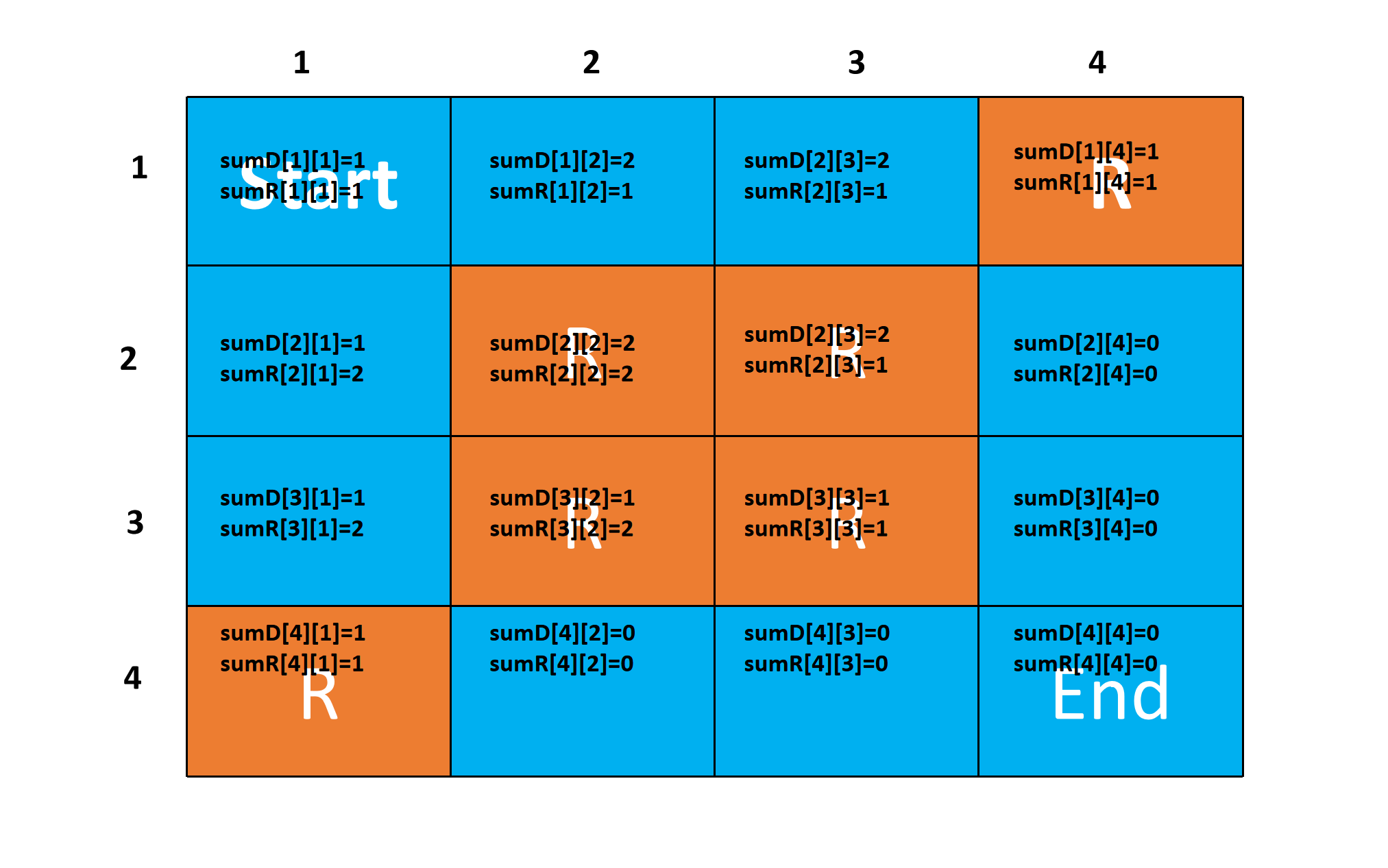
计算岩石总数前缀和

• 看到如上的累加公式，我们很容易想到要用前缀和来处理。否则时间复杂度会升到立方。
  
  我们令$$ sumD[i][j] = sumD[i][j + 1] + dpD[i][j], \ sumR[i][j] = sumR[i + 1][j] + dpR[i][j].$$
  
  则原公式可优化为$$\begin{cases}dpD[n][m] = dpR[n][m] = 1, \dpD[i][j] = \sum_{t=i + 1}^{n - numD[i][j]}dpR[t][j] = sumR[i + 1][j] - sumR[n - numD[i][j] + 1][j], \ dpR[i][j]= \sum_{t=j + 1}^{m - numR[i][j]}dpD[i][t] = sumD[i][j + 1] - sumD[i][m - numR[i][j] + 1] \end{cases}.$$

• 最后答案即为\(dpD[1][1] + dpR[1][1]\)，注意随时取模。

• 存在两种情况需要特判，详见代码。

以第三个样例为例试举两例，



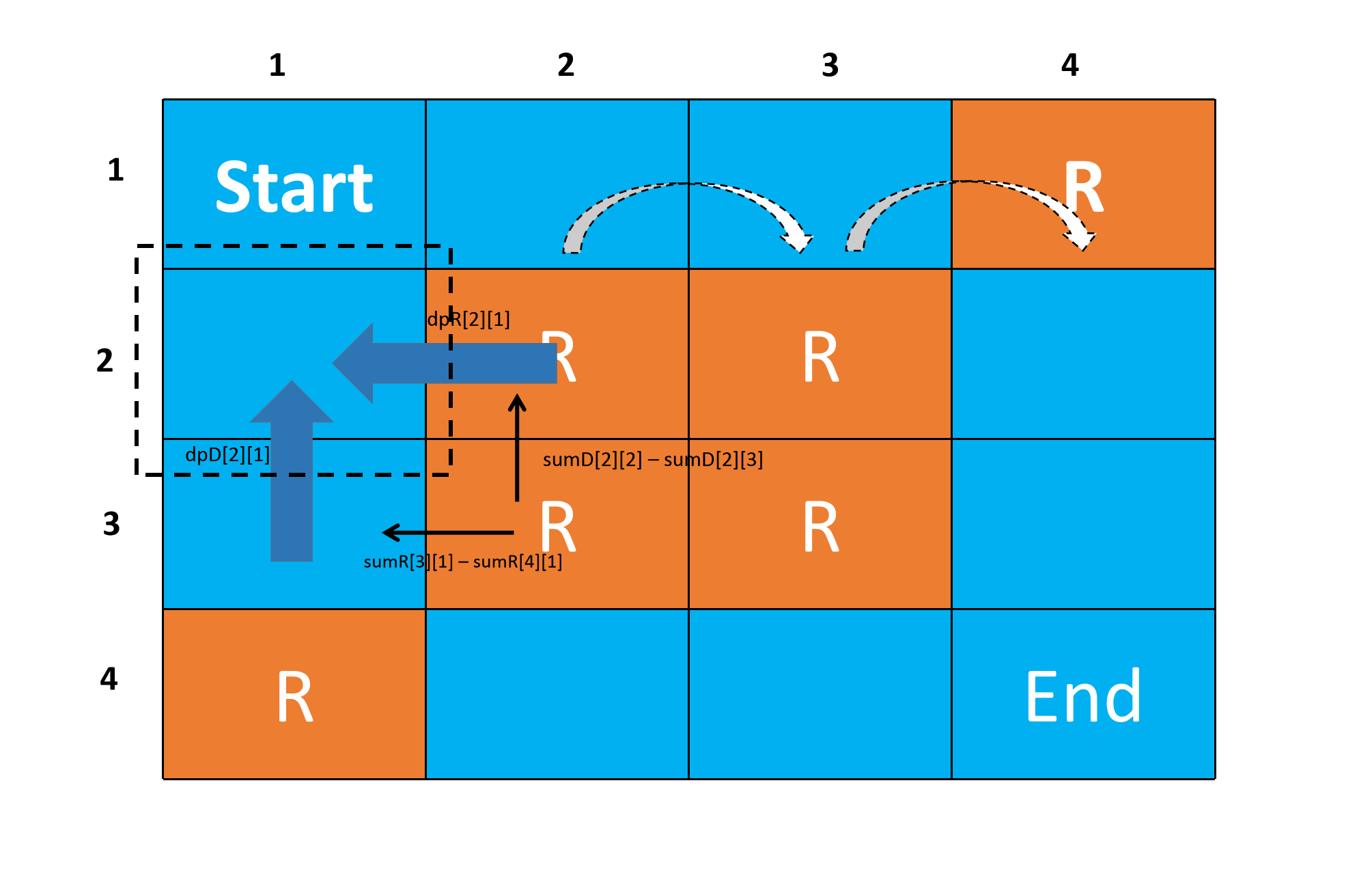
计算（2,1）的\(dpD\)和\(dpR\)



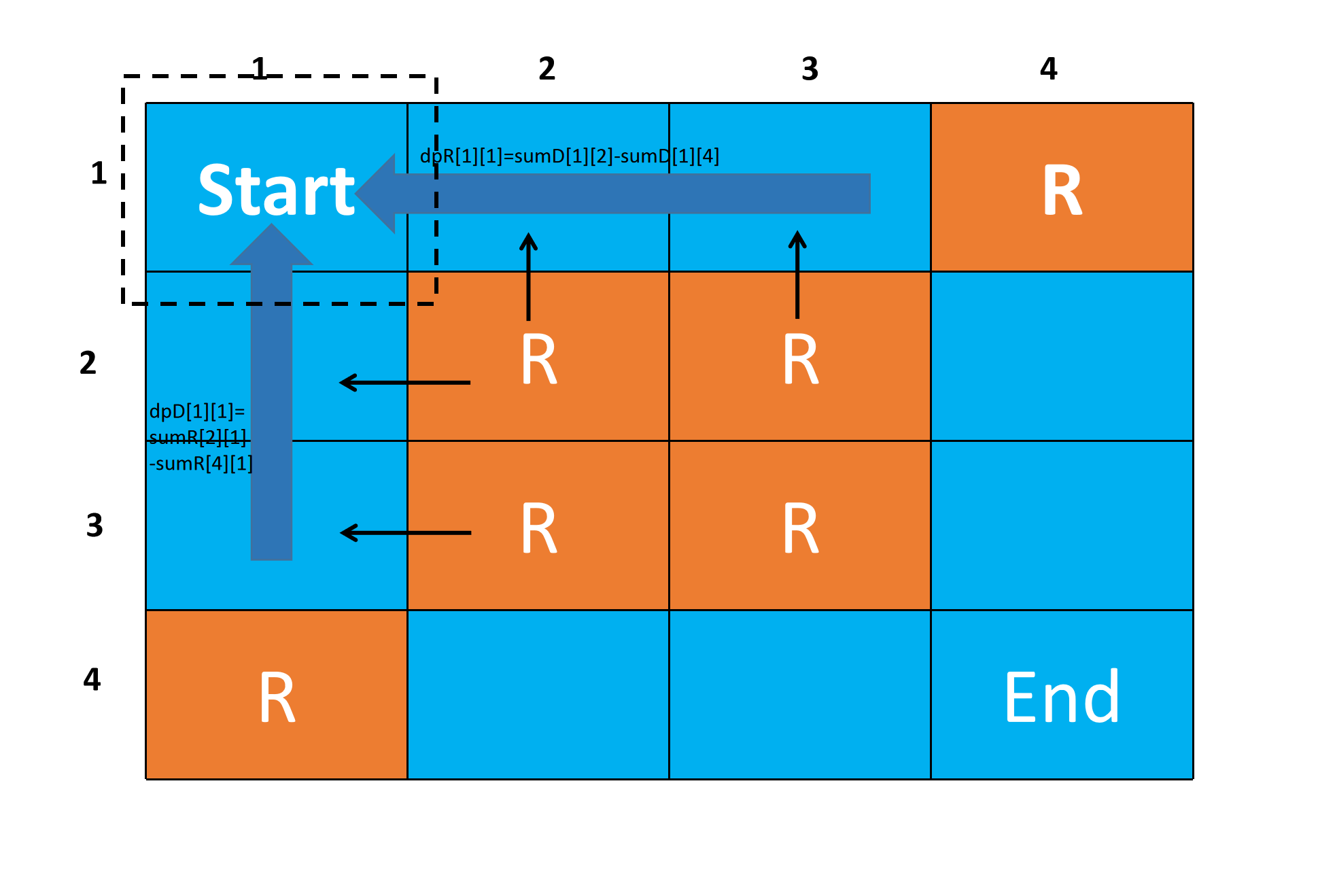
计算（1,1）的\(dpD\)和\(dpR\)

---

通过代码

/*
Status
	Accepted
Time
	108ms
Memory
	102804kB
Length
	1284
Lang
	GNU G++11 5.1.0
Submitted
	2019-12-23 18:13:00
RemoteRunId
	67463663
*/

#include <bits/stdc++.h>
using namespace std;

const int MOD = 1e9 + 7;      //随时取模.
const int MAXN = 2e3 + 50;

char s[MAXN][MAXN];
int  numD[MAXN][MAXN], numR[MAXN][MAXN], sumD[MAXN][MAXN], sumR[MAXN][MAXN], dpD[MAXN][MAXN], dpR[MAXN][MAXN];
int n, m;

int main()
{
    scanf("%d%d", &n, &m);

    for(int i = 1; i <= n; i ++)
        scanf("%s", s[i] + 1);

    if(s[1][1] == 'R' || s[n][m] == 'R'){        //第一种特判情况，起点或终点被岩石占上，则没有路径可以到达.
        printf("0");
        return 0;
    }

    if(n == 1 && m == 1){                       //第二种特判情况，地图大小为1*1，则直接输出1.
        printf("1");
        return 0;
    }

    for(int i = n; i >= 1; i --){              //从右下开始预处理岩石总数前缀和.
        for(int j = m; j >= 1; j --){
            numD[i][j] = numD[i + 1][j] + (s[i][j] == 'R');
            numR[i][j] = numR[i][j + 1] + (s[i][j] == 'R');
        }
    }

    sumD[n][m] = sumR[n][m] = dpD[n][m] = dpR[n][m] = 1;
    for(int i = n; i >= 1; i --){                   //从右下开始状态转移.
        for(int j = m; j >= 1; j --){
         if(i == n && j == m)   continue;
        dpD[i][j] = (sumR[i + 1][j] - sumR[n - numD[i + 1][j] + 1][j]) % MOD;
        dpR[i][j] = (sumD[i][j + 1] - sumD[i][m - numR[i][j + 1] + 1]) % MOD;

        sumD[i][j] = (sumD[i][j + 1] + dpD[i][j]) % MOD;
        sumR[i][j] = (sumR[i + 1][j] + dpR[i][j]) % MOD;
        }
    }

    printf("%d", (dpR[1][1] + dpD[1][1] + 2ll * MOD) % MOD);            //得出答案.
    return 0;
}

---