网络流强化-HDU 3338-上下界限制最大流

　　题意是：

　　一种特殊的数独游戏，白色的方格给我们填1-9的数，有些带数字的黑色方格，右上角的数字代表从他开始往右一直到边界或者另外一个黑格子，中间经过的白格子的数字之和要等于这个数字；左下角的也是一样的意思，只是作用对象成了它下方的白格子。

　　思路：

　　既然所有行的数字之和等于所有列的数字之和，那么我们可以将行方向（向右）的点作为与源点连接的点，列方向（向下）的点作为与汇点连接的点。

　　由于向右和向下的点可能在同一块方格里面，以及我们需要设置每个白格子的容量，所以我们需要拆点。

　　题目要求填1-9的数，所以白格子起码都是1，我们不妨假设这些基础的1已经填好了，那么将对应行方向的点的入边（来自源点）容量减去该点作用范围内的白格子数目，将对应列方向的点的出边（去到汇点）容量减去该点作用范围内的白格子数目。然后设置白格子的容量为8就能保证填的都是1-9的数了。

　　

 #include<cstdio>
 #include<cstring>
 #include<cmath>
 using namespace std;
 #define maxe 100128  //pay  双向边 一共10万条路 双向就是20万 反边就是40万
 #define maxv 20128   //pay
 #define maxn 105    //pay
 #define sc scanf
 #define pt printf
 #define rep(i,a,b)  for(int i=(a);i<(b);++i)
 const int inf = 0x3f3f3f3f;
 int cg,sp,ins;  //cg change sp是总流量 ins是加速回溯点
 int N,M,s,t,delta,UP_LIMIT;
 int q[maxv],fro,rea;
 typedef struct ed{
     int v,nxt,cap; //dis
 }ed;
 ed e[maxe];
 int tot,head[maxv],cur[maxv],vis[maxv],bk[maxv],d[maxv],num[maxv]; //
 int mi(int a,int b) {return a<b?a:b;}
 int mx(int a,int b) {return a>b?a:b;}
 void add(int u,int v,int cap)
 {
     e[tot].v=v;         e[tot].nxt=head[u];
     /*e[tot].dis=dis;*/     e[tot].cap=cap;
     head[u]=tot++;

     e[tot].v=u;         e[tot].nxt=head[v];
     /*e[tot].dis=-dis;*/    e[tot].cap=;
     head[v]=tot++;
 }
 // 仅有一次的BFS为ISAP节省了不少时间
 bool bfs()
 {
     //数组模拟queue
     int u,v,i,my_all = t;
     for(i=;i<=my_all;++i) vis[i]=num[i]=;  //无须一定是my_all，涉及所有即可~~~~~~~~~~~~~~~~~~
     for(i=;i<=my_all;++i) d[i]=UP_LIMIT;    //UP_LIMIT的设定是比最高的层次大1
     fro = rea = ;
     q[rea] = t; ++rea;
     vis[t] = ;
     d[t] = ;
     ++num[d[t]];
     while (rea>fro)
     {
         u = q[fro]; ++fro;
         //pt("BFSing~ : u=%d\n",u);
         for (i=head[u]; i!=-; i=e[i].nxt)
         {
             v=e[i].v;
             if (!vis[v] && e[i^].cap )
             {
                 vis[v] = true;
                 d[v] = d[u] + ;
                 ++num[d[v]];
                 q[rea] = v; ++rea;
                 //pt("普度众生 u=%d,v=%d,d[u]=%d,d[v]=%d\n",u,v,d[u],d[v]);
             }
         }
     }
     //int last_ed=-1;
     //把连接了到不了终点的点的边都去除 如果确定都能和终点连接 就不需要
     /*for(u=0;u<=my_all;++u)
     {
         if(!vis[u]) continue;
         for (i=head[u]; i!=-1; i=e[i].nxt)
         {
             v=e[i].v;
             if(!vis[v])
             {
                 if(i==head[u]){
                     head[u] = e[i].nxt;
                     continue;
                 }
                 else{
                     e[last_ed].nxt = e[i].nxt;
                     continue;
                 }
             }
             last_ed = i;
         }
     }*/
     return vis[s];
 }
 // 增广
 int augment()/*单源单汇 不用查这个*/
 {
     int  flow = inf, i;
     cg = t;
     // 从汇点到源点通过 p 追踪增广路径, flow 为一路上最小的残量
     while (cg != s) {
         i = bk[cg];
         if(flow>=e[i].cap)
         {
             flow = e[i].cap;
             ins = e[i^].v;
             //用来加速寻找，在最小流量断开的地方重新开始寻找
             //嗯，等一下 我这个是从终点往起点寻找，而确定增光路径是从起点到终点
             //那么起点是河流的上游，那么回溯的河段应该尽可能的往上游靠近
             //所以应该将flow>e[i].cap的大于号改成大于等于号
         }
         cg = e[i^].v;
     }
     cg = t;
     // 从汇点到源点更新流量
     while (cg != s) {
         i = bk[cg];
         e[i].cap -= flow;
         e[i^].cap += flow;
         cg = e[i^].v;
     }
     return flow;
 }
 //由于每次修改层次的时候，都是在到剩下子节点的距离中挑选最短的加1 所以层次分明不会出现死循环
 int max_flow()
 {
     int flow = ,i,u,v;
     bool advanced;
     if(bfs()==false) return ;
     //pt("零层妖塔=%d\n",d[s]);
     u = s;
     memcpy(cur, head, sizeof(head));
     while (d[s] < UP_LIMIT)          //UP_LIMIT的设定是比最高的层次大1
     //终点是0，那么起点所在层次最多是N-1 同理，不是d[s]<t
     {
         if (u == t)
         {
             flow += augment();
             u = ins;    //pay speed up
         }
         advanced = false;
         for (i = cur[u]; i!=-; i=e[i].nxt)
         {
             v = e[i].v;
             //pt("SELECT: %d -> %d\n",u,v);
             if (e[i].cap && d[u] == d[v] + )
             {
                 advanced = true;
                 bk[v] = i;
                 cur[u] = i;
               //  pt("%d -> %d ::d[u]=%d,d[v]=%d\n",u,v,d[u],d[v]);
                 u = v;
                 break;
             }
         }
         if (!advanced)
         { // retreat
             int base = UP_LIMIT;        //UP_LIMIT的设定是比最高的层次大1
             for (i = head[u]; i != -; i=e[i].nxt)
             {
                 if (e[i].cap&&base>d[e[i].v])
                 {
                     cur[u] = i;
                     base = d[e[i].v];
                 }
             }

             if (--num[d[u]] == )
             {
                 //pt("u=%d,d=%d\n",u,d[u]);
                 //pt("BREAK FROM HERE\n");
                 break; // gap 优化
             }
             ++num[d[u] = base+];
             //pt("------------------我来增加层次%d：%d\n",m+1,u);
             //我以前一直在想 如果没有找到怎么办呢 现在发现原来找不到的话距离会被赋成base+1
             //—— 比上界还高 所以接下来不会再访问到这个点 这个点也没有机会被减成0了——不会莫名其妙地break，哈哈哈
             if (u != s)
             {
                 //pt("from %d ",u);
                 u = e[bk[u]^].v;
                 //pt("return to %d\n",u);
             }
             else
             {
                 // pt("STILL AT S:%d\n",s);
             }
         }
     }
     return flow;
 }

 void init()
 {
     tot=;
     memset(head,-,sizeof(head));   //pay
 }
 char info[maxn][maxn][];
 int  ok_ed[maxn][maxn];
 int is_black[maxn][maxn];
 int LEFT[maxn][maxn],RIGHT[maxn][maxn];
 //最大流部分没有什么问题了 关键在于终点源点、编号分配、题目理解建图上面
 //切记：不要建立无用的边！！ 包括连接不到的点 和不和终点连通的点
 //确保所有的点都要和终点连通——这样才是合法的点
 int main()
 {
     freopen("in.txt","r",stdin);

     /*数据初始化区*/
     s=, bk[]=-;

     /*变量存放区*/
     int i,j,u,v,id,who,sub;

     while(~sc("%d%d",&N,&M))
     {

         /*数据初始化区*/
         init(); sp = ;
         for(i=;i<N;++i) for(j=;j<M;++j) is_black[i][j] = ;
         for(i=;i<N;++i) for(j=;j<M;++j) LEFT[i][j] = RIGHT[i][j] = ok_ed[i][j] = -;

         /*数据读取区*/
         for(i=;i<N;++i) for(j=;j<M;++j) sc("%s",info[i][j]);

         /*关键数据赋值区*/
         delta  = (N)*(M); t=*delta+; s=*delta;
         UP_LIMIT = *delta + ;
                 //说明：这个是层次的无法达到的上界，所以一共有N个点的时候，
                 //如果从0开始编号，那么上界就是N；如果从1开始编号，上界就是N+1

         /*数据处理区*/ /*建图区*/
         for(i=;i<N;++i) for(j=;j<M;++j)
         {
             if(info[i][j][]=='.')  continue;
             is_black[i][j] = ;
             if(info[i][j][]!='X')  LEFT[i][j] = (info[i][j][]-'')*+(info[i][j][]-'')*+info[i][j][]-'';
             if(info[i][j][]!='X') RIGHT[i][j] = (info[i][j][]-'')*+(info[i][j][]-'')*+info[i][j][]-'';
         }
         for(i=;i<N;++i) for(j=;j<M;++j)
         {
             if(is_black[i][j]==)  continue;
             if(LEFT[i][j]==-&&RIGHT[i][j]==-) continue;

             if(LEFT[i][j]!=-)
             {
                 id = i*M + j + delta; //往下的取小一点的编号
                 v=j; u=i+; sub = ;
                 while(u<N&&is_black[u][v]==) ++sub,++u;
                 LEFT[i][j]-=sub;
                 add(id,t,LEFT[i][j]);
             }
             if(RIGHT[i][j]!=-)
             {
                 id = i*M + j ; //往下的取小一点的编号
                 u=i; v=j+;  sub=;
                 while(v<M&&is_black[u][v]==) ++sub,++v;
                 RIGHT[i][j]-=sub;
                 add(s,id,RIGHT[i][j]);
             }
         }
         for(i=;i<N;++i) for(j=;j<M;++j)
         {
             if(is_black[i][j])  continue;
             id = i*M +j;            //!!!居然把这个放在后面，那建立边就会失败了，相当于用这次的容量帮上次的建边
             add(id,id+delta,); ok_ed[i][j] = tot - ; //value[i][j] - cap就是分配的流量 

             /*OUTPUT*/
             v=j; u=i-;
             while(is_black[u][v]==) --u;
             who = u*M + v;
             add(id+delta,who+delta,inf);
             /*INPUT*/
             u=i; v=j-;
             while(is_black[u][v]==) --v;
             who = u*M + v ;
             add(who,id,inf);
         }
         /*答案处理区*/
         sp = max_flow();
         //pt("sp=%d\n",sp);
         for(i=;i<N;++i) for(j=;j<M;++j)
         {
             if(j>) pt(" ");
             if(is_black[i][j]==) pt("_");
             else
             {
                 who = ok_ed[i][j];
                 pt("%d",  - e[who].cap   ); 

             }
             if(j==M-) pt("\n");
         }
     }
     return ;
 }

 /**
  * 友情链接：
  * http://www.renfei.org/blog/isap.html 解释ISAP原理
  * https://www.cnblogs.com/bosswnx/p/10353301.html 使用的数据结构和我的比较相近
  */

HDU 3338 ISAP

　　2019年8月18日17:11:56

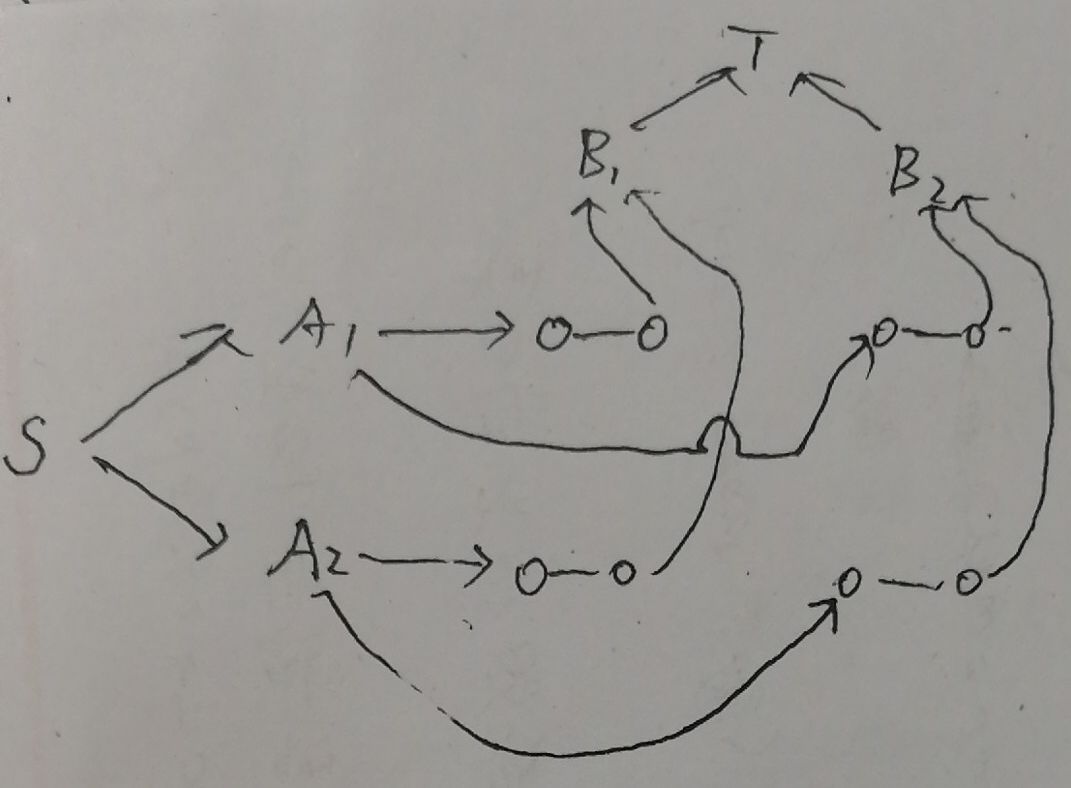
　　想要知道这个增广大概是怎么回事，因为我之前觉得好像都是线性的。

　　假设先走S->A1->B1->T，之后B1->T已经满流，此时再走S->A2->B1->T，走不通了。

　　那么可以从B1往回增广走到A1，然后从A1开始增广寻找新的路径，如A1->B2->T。