HDU 1007(套圈 最近点对距离)

题意是求出所给各点中最近点对的距离的一半（背景忽略）。

用分治的思想，先根据各点的横坐标进行排序，以中间的点为界，分别求出左边点集的最小距离和右边点集的最小距离，然后开始合并，分别求左右点集中各点与中间点的距离，从这些距离与点集中的最小距离比较，求得最小距离，此处可按纵坐标排序，将纵坐标距离已经大于之前最小距离的部分都剪枝。

代码如下：

 #include <bits/stdc++.h>
 using namespace std;
 int n,a[];
 struct point
 {
     double x,y;
 }p[];
 bool cmpx(point a,point b)
 {
     return a.x < b.x;
 }
 bool cmpy(int a,int b)
 {
     return p[a].y < p[b].y;
 }
 double dis(point a,point b)
 {
     return sqrt( (a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y) );
 }
 double min(double a,double b,double c)
 {
     if(a>b) return b>c?c:b;
     return a>c?c:a;
 }
 double fin(int from,int to)
 {
     if(from+ == to ) return dis(p[from],p[to]);
     if(from+ == to ) return min(dis(p[from],p[from+]),dis(p[from],p[to]),dis(p[from+],p[to]));
     int mid = (from+to)>>;
     double ans = min(fin(from,mid),fin(mid+,to));
     int cnt = ;
     for(int i = from; i <= to; i++)
         if(abs(p[i].x-p[mid].x) <= ans) a[cnt++] = i;
     sort(a,a+cnt,cmpy);
     for(int i = ; i < cnt; i++)
         for(int j = i+; j < cnt; j++)
         {
             if(p[a[j]].y-p[a[i]].y >= ans) break;
             ans = min(ans,dis(p[a[i]],p[a[j]]));
         }
     return ans;
 }
 int main()
 {
     while(scanf("%d",&n)&&n)
     {
         for(int i = ; i < n; i++)
             scanf("%lf %lf",&p[i].x,&p[i].y);
         sort(p,p+n,cmpx);
         printf("%.2lf\n",fin(,n-)/);
     }
     return ;
 }

但是呢，开始时本人并不是这么写的，而是求了所有点中最小的横坐标和纵坐标，然后以此为参照点，分别求其他各点到参照点的距离，以距离排序，再求出相邻两点距离的最小值。这么写是上面写法的用时一半左右，尽管 AC 了，但是这么写是不对的......

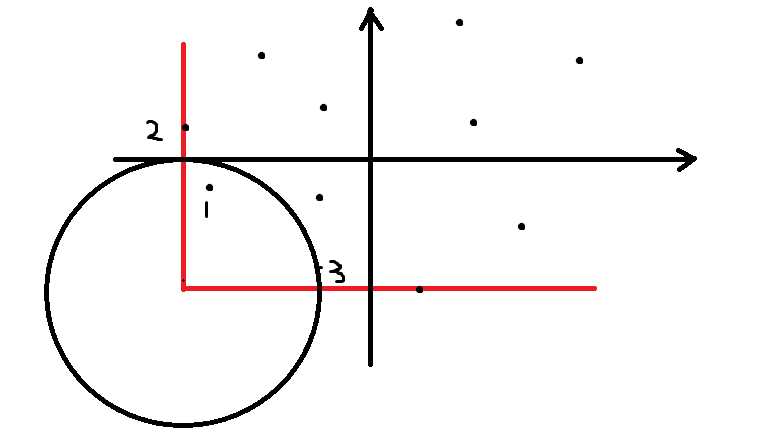
如图所示，图中的点 1 和点 2 距离比点 1 和点 3 的距离更近，但是第二种方法则是用点 1 和点 3距离与点 3 和点 2 距离中求较小值。（题目的测试数据中可能没有这样的数据吧......）

第二种方法的代码如下：

 #include <bits/stdc++.h>
 using namespace std;
 int n;
 struct point
 {
     double x,y,dis;
 }st,p[];
 bool cmp(point a,point b)
 {
     if(a.dis!=b.dis) return a.dis < b.dis;
     return a.x<b.x;
 }
 double dist(point a,point b)
 {
     return sqrt( (a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y) );
 }
 int main()
 {
     double sml;
     while(scanf("%d",&n)&&n)
     {
         st.x = st.y = 1000000.0;
         sml = 1000000.0;
         for(int i = ; i < n; i++)
         {
             scanf("%lf %lf",&p[i].x,&p[i].y);
             if(p[i].x < st.x) st.x = p[i].x;
             if(p[i].y < st.y) st.y = p[i].y;
         }
         for(int i = ; i < n; i++)
             p[i].dis = dist(p[i],st);
         sort(p,p+n,cmp);
         for(int i = ; i < n; i++)
             if(dist(p[i],p[i-])<sml) sml = dist(p[i],p[i-]);
         printf("%.2lf\n",sml/);
     }
     return ;
 }