hdu 5521 Meeting（最短路）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=5521

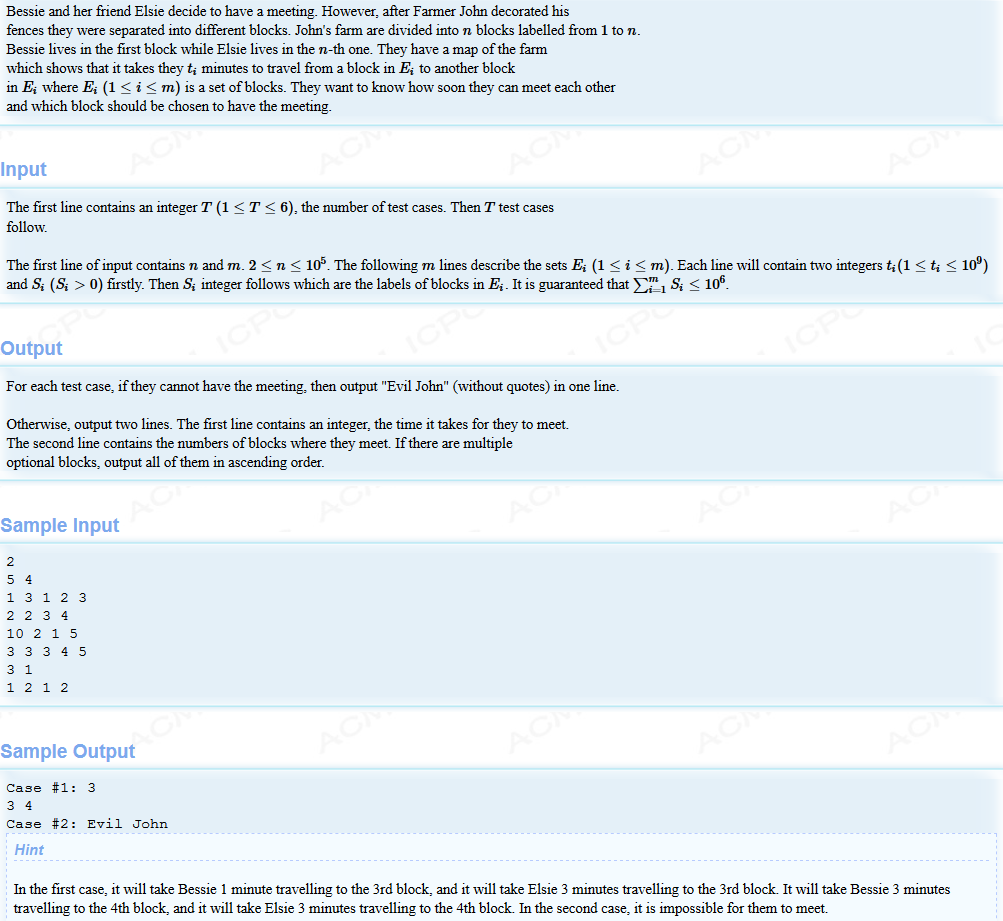
题意：有1-n共n个点，给出m个块（完全图），并知道块内各点之间互相到达花费时间均为ti。已知两人分别在点1和点n，求在哪些点相遇能使得花费时间最短。

题解：显然先想到从点1和点n分别求最短路，然后枚举点找出哪些点是相遇花费时间最少的。但是这题边太多了，假设一个完全图里有x个点，那边就有x*(x-1)/2条了，必须化简其边。一个可行的办法是给每个完全图增加两个点，分别为入点和出点，入点向其中的点连边，其中的点再向出点连边，权均为0，出点向入点连边，权为ti，边数就化简为2*x了。
代码实现：

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const ll INF = 1e18;
 const int N = ;
 const int M = ;
 struct edge {
     int to;
     ll cost;
     edge(int _to, ll _cost):to(_to),cost(_cost){}
 };
 typedef pair<ll, int> P;// first是最短距离，second是顶点的编号
 int V;
 vector<edge>G[N];
 ll d[][N];//点1 和 点n 到达其他点的最短时间
 void dij(int id, int s) {
     priority_queue<P, vector<P>, greater<P> > que;
     for(int i = ; i <= V; ++i) d[id][i] = INF;
     d[id][s] = ;
     que.push(P(, s));

     while(!que.empty()) {
         P p = que.top(); que.pop();
         int v = p.second;
         if(d[id][v] < p.first) continue;
         int num = G[v].size();
         for(int i = ; i < num; ++i) {
             edge e = G[v][i];
             if(d[id][e.to] > d[id][v] + e.cost) {
                 d[id][e.to] = d[id][v] + e.cost;
                 que.push(P(d[id][e.to], e.to));
             }
         }
     }
 }
 int main() {
     int k, T, t, n, m, i, s, x, u, v;
     scanf("%d", &T);
     for(k = ; k <= T; ++k) {
         for(i = ; i < N; ++i) G[i].clear();
         scanf("%d%d", &n, &m);//点数，集合(完全图)数目
         for(i = ; i <= *m; i += ) {
             u = n+i;//入点
             v = n+i+;//出点
             scanf("%d%d", &t, &s);//时间，集合中点数
             while(s--) {
                 scanf("%d", &x);
                 G[u].push_back(edge(x, ));
                 G[x].push_back(edge(v, ));
             }
             G[v].push_back(edge(u, t));
         }
         V = n+*m;
         dij(, );
         dij(, n);
         /*
         puts("-----------------");
         for(i = 1; i <= n; ++i) {
             printf("%lld, %lld\n", d[0][i], d[1][i]);
         }
         puts("-----------------");
         */
         ll mi = INF;
         int cnt = ;
         ll a = ;
         for(i = ; i <= n; ++i) {
             if((a = max(d[][i], d[][i])) < mi) {
                 mi = a;
             }
         }
         printf("Case #%d: ", k);
         if(mi == INF) {
             printf("Evil John\n");
         }
         else {
             int f = ;
             printf("%lld\n", mi);
             for(i = ; i <= n; ++i) {
                 a = max(d[][i], d[][i]);
                 if(a == mi) {
                     if(f) putchar(' ');
                     printf("%d", i);
                     f = ;
                 }
             }
             puts("");
         }
     }
     return ;
 }

2667ms