机器学习实战python3 Logistic Regression

代码及数据：https://github.com/zle1992/MachineLearningInAction

logistic regression

优点:计算代价不高，易于理解实现，线性模型的一种。

缺点:容易欠拟合，分类精度不高。但是可以用于预测概率。

适用数据范围:数值型和标称型。

准备数据：

 def loadDataSet():
     dataMat,labelMat = [],[]
     with open(filename,"r") as  fr:  #open file
         for line in fr.readlines():
             lineArr = line.split() #split each line
             dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])  #创建2维list
             labelMat.append(int(lineArr[2]))
     return dataMat,labelMat

1  基于Logistic回归和Sigmoid函数的分类

Sigmoid函数：

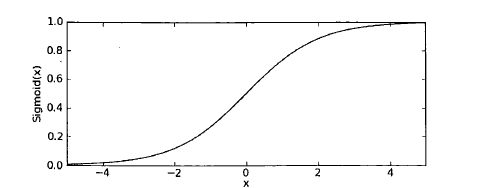
 def sigmoid(inX):
     return 1.0/(1+np.exp(-inX))

2基于最优化方法的最佳回归系数确定

梯度上升法：

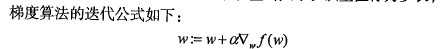
梯度上升法的伪代码如下:
每个回归系数初始化为1
重复R次:
计算整个数据集的梯度
使用alpha x gradient更新回归系数的向量
返回回归系数

代码：

 def sigmoid(inX):
     return 1.0/(1+np.exp(-inX))

 def gradAscent(dataMat,labelMat):
     dataMatrix = np.mat(dataMat)  #translate list to matrix
     labelMatrix = np.mat(labelMat).transpose() #转置
     m,n = np.shape(dataMatrix) #100 rows  3 coulums
     alpha = 0.001 #步长 or 学习率
     maxCyclse = 500
     weight = np.ones((n,1)) #初始值随机更好吧
     #weight = np.random.rand(n,1)
     for k in range(maxCyclse):
         h = sigmoid(dataMatrix * weight) # h 是向量
         error = (labelMatrix - h)  #error 向量
         weight = weight + alpha * dataMatrix.transpose() *error  #更新
      #   print(k,"  ",weight)
     return weight

3分析数据:画出决策边界

 def plotfit(wei):
     import matplotlib.pyplot as plt
     weight = np.array(wei) #???????? #return array
     dataMat ,labelMat = loadDataSet()
     dataArr = np.array(dataMat)
     n = np.shape(dataArr)[0]  #row
     fig = plt.figure()   #plot
     ax = fig.add_subplot(111)
     ax.scatter(dataArr[:,1],dataArr[:,2],s =50, c = np.array(labelMat)+5) #散点图 #参考KNN 的画图
     x = np.arange(-3.0,3.0,0.1)   #画拟合图像
     y = (-weight[0] - weight[1] *x ) / weight[2]
     ax.plot(x,y)
     plt.xlabel("x1")
     plt.ylabel("x2")
     plt.show()

4训练算法:随机梯度上升

伪代码:
所有回归系数初始化为1
对数据集中每个样本
计算该样本的梯度
使用alpha x gradient更新回归系数值
返回回归系数值

原始梯度上升计算数据集的梯度，涉及的是矩阵运算。h,error都是向量

随机梯度算法计算的是数据集中每个样本的梯度，s计算量减小，h,error都是数值

 ef stocGradAscent0(dataMatrix,labelMatrix):
     m,n = np.shape(dataMatrix)
     alpha = 0.1
     weight = np.ones(n)
     for i in range(m):
         h = sigmoid(sum(dataMatrix * weight))
         error = labelMatrix[i] - h
         weight = weight + alpha * error * dataMatrix[i]
     return weight

上面的算法是固定的步长，固定的步长，不稳定，会产生震荡，所以下面的算法采用不固定的步长。

距离目标值远的时候，步长大，距离目标值近的时候，步长小。

 def stocGradAscent1(dataMat,labelMat,numIter = 150):
     dataMatrix = np.mat(dataMat)  #translate list to matrix
     labelMatrix = np.mat(labelMat).transpose() #转置
     m,n = np.shape(dataMat)
     alpha = 0.1
     weight = np.ones(n) #float
     #weight = np.random.rand(n)
     for j in range(numIter):
         dataIndex = list(range(m)) #range 没有del 这个函数　　所以转成list  del 见本函数倒数第二行
         for i in range(m):
             alpha = 4/(1.0 +j + i) + 0.01
             randIndex = int(np.random.uniform(0,len(dataIndex))) #random.uniform(0,5) 生成0-5之间的随机数
             #生成随机的样本来更新权重。
             h = sigmoid(sum(dataMat[randIndex] * weight))
             error = labelMat[randIndex] - h
             weight = weight + alpha * error * np.array(dataMat[randIndex])  #!!!!一定要转成array才行
             #dataMat[randIndex] 原来是list  list *2 是在原来的基础上长度变为原来2倍，
             del(dataIndex[randIndex]) #从随机list中删除这个
     return weight

5从病气病症预测病马的死亡率

 def classifyVector(inX,weight):  #输入测试带测试的向量 返回类别
     prob = sigmoid(sum(inX * weight))
     if prob > 0.5 :
         return 1.0
     else: return 0.0
 def colicTest():
     trainingSet ,trainingSetlabels =[],[]
     with open("horseColicTraining.txt") as frTrain:
         for lines in frTrain.readlines():
             currtline = lines.strip().split('\t')  # strip()remove the last string('/n') in everyline
             linearr = [] #每行临时保存str 转换float的list
             for i in range(21):   #将读进来的每行的前21个str 转换为float
                 linearr.append(float(currtline[i]))
             trainingSet.append(linearr)  #tianset 是2维的list
             trainingSetlabels.append(float(currtline[21]))#第22个是类别
     trainWeights = stocGradAscent1(trainingSet,trainingSetlabels,500)
     errorCount = 0
     numTestVec = 0.0
     with open("horseColicTest.txt") as frTrain:
         for lines in frTrain.readlines():
             numTestVec += 1.0
             currtline = lines.strip().split('\t')  # strip()remove the last string('/n') in everyline
             linearr = []  #测试集的每一行
             for i in range(21):
                 linearr.append(float(currtline[i]))#转换为float
             if int(classifyVector(np.array(linearr),trainWeights)) != int(currtline[21]) :
                 errorCount += 1  #输入带分类的向量，输出类别，类别不对，errorCount ++
             errorRate = float(errorCount)/numTestVec
             print("the error rate of this test is : %f"%errorRate)
     return errorRate
 def multiTest(): #所有测试集的错误率
     numTests = 10
     errorSum = 0.0
     for k in range(numTests):
         errorSum +=colicTest()
     print("after %d iterations the average error rate is : %f" %(numTests,errorSum/float(numTests)))

主函数:

 if __name__ == '__main__':
     filename = "testSet.txt"
     dataMat,labelMat = loadDataSet()
     #weight = gradAscent(dataMat,labelMat)
     weight = stocGradAscent1(dataMat,labelMat)
     print(weight)
     plotfit(weight)#画分类图像在小数据集上
     multiTest() #真实数据集上测试