1：如果格式不正确，导入题录失败的话，可以手动添加。点击新建题录即可。输入文章的标题等信息。

2：导入word中的文献，可以使用word中notefirst的引文编辑功能，对文献进行删除，编辑等。

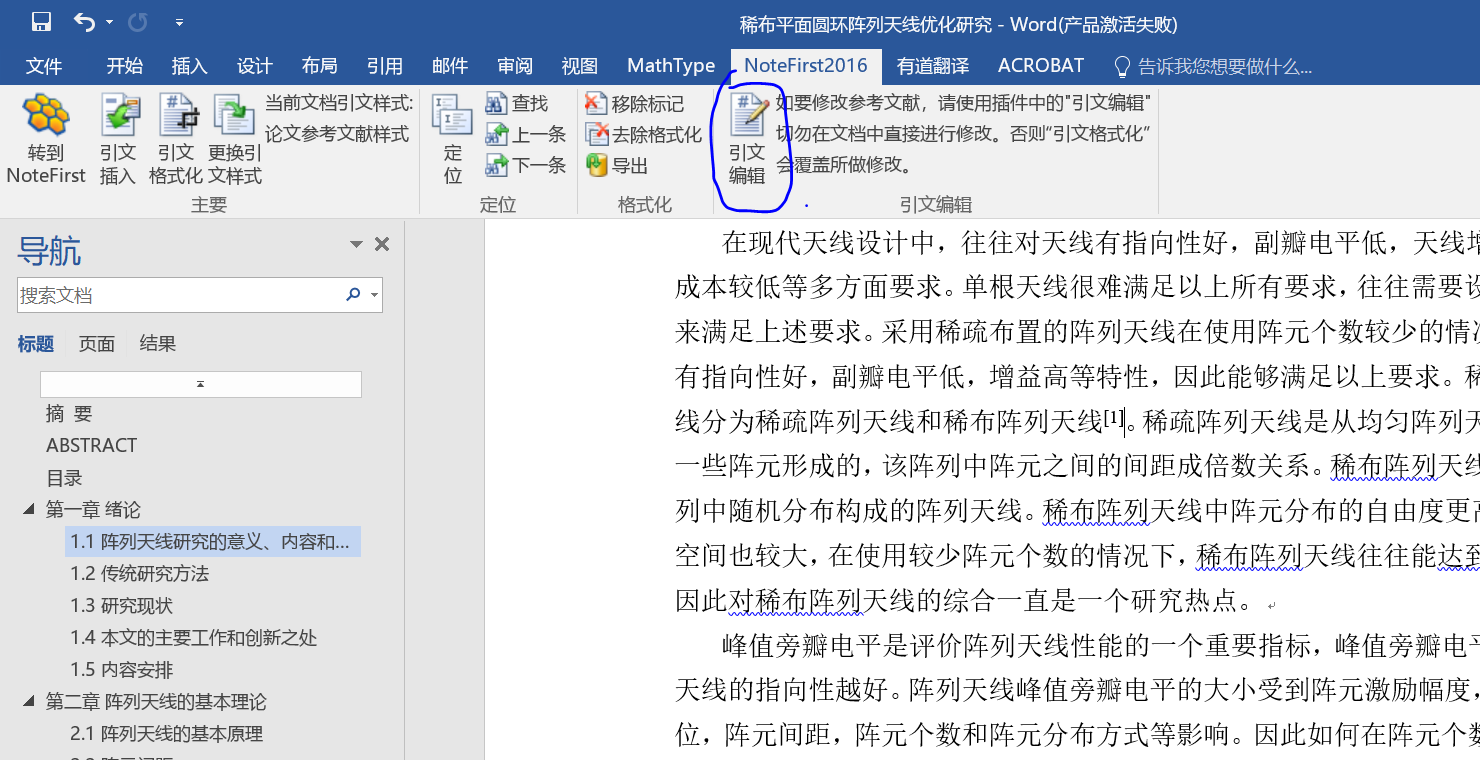
3：如果notefirst中，如果添加的文献，缺失一些内容，选中该文献，右键》编辑题录。

4：将引文与文章对齐，选中引文，点击：开始》x2

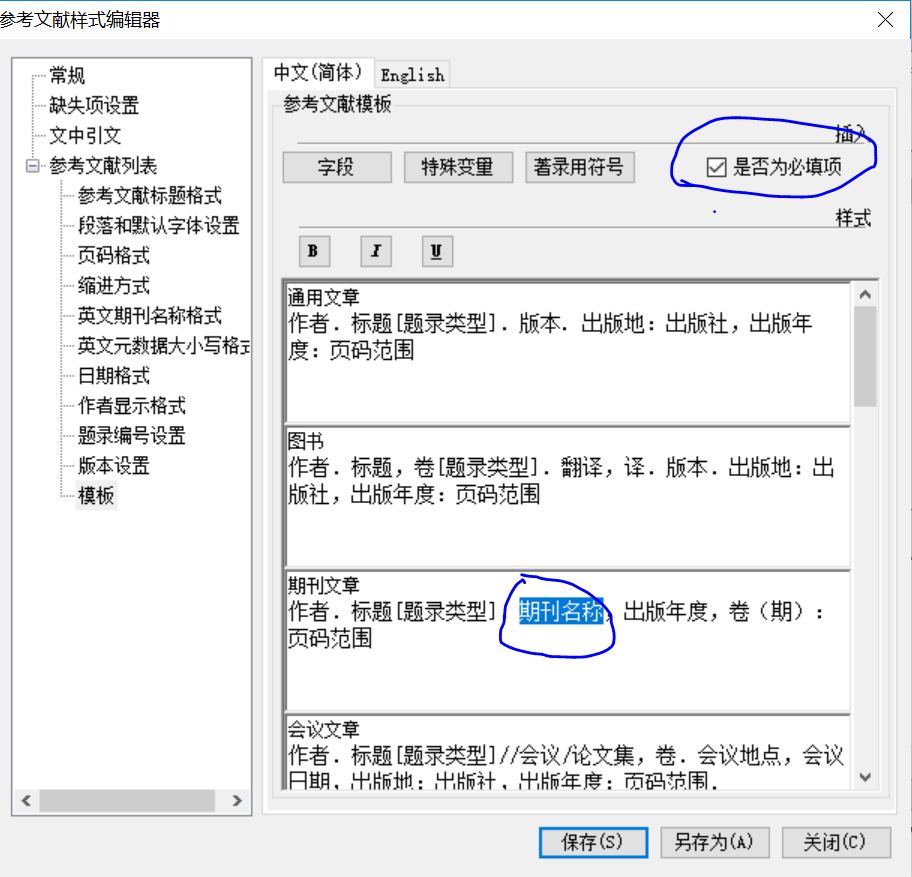
5：文献中某个字段是否必填，如果选为不是必填项，那么缺失也正常显示。

notefirst使用的更多相关文章

  1. 谷歌chrome 插件（扩展）开发——进阶篇（c#本地程序和插件交互）下

    在上一篇中,我提出了总任务.接下来去实现. 获取网页内容等其它信息,这是content.js 擅长做的事情: chrome.extension.onMessage.addListener( funct ...

  2. vsto下开发wps插件

    我们要开发wps插件了.之前用vsto开发过word插件,我也讲过c#下如何开发wps插件(有点繁琐).如果采用c#从头再开发wps插件,那么开发出来的office加载项就会出现两个.我们要实现的wp ...

  3. c#多线程同步之EventWaitHandle的应用

    最近在研究前辈写的winform代码,其中有一个功能,前辈用了EventWaitHandle.初读代码,有点不理解,慢慢想来,还是可以理解的.这个功能,就是执行某项比较耗时的任务,需要打开旋转图标,等 ...

  4. c# winform中的一段代码赏析

    我遇到了一个bug,是客户测试我们的产品,报出来的,而且有异常信息文件,这对于定位问题,很有帮助. 我找到源码看了下,bug还无法重现.于是我随便点点客户端,经过了几次调试,结果报出错误来了.客户端界 ...

  5. .Net core,EFCore 入门

    我在百度上搜了一下.net  core和efcore 入门案例.好多博客都是大概说了一下做法,对于小白而言还是一头雾水,我今天就抽出一点时间,写一个详细的入门小案例,就一张表没有什么业务可言.主要是操 ...

  6. .net remoting和wcf自托管——一个bug引发的警示

    一.解决问题,需要深入,并从细节入手,多从代码找原因,不能认为代码是死的,不会出错: 之前代码都运行良好,突然某一天,在我电脑上出问题了.出了问题,那就应该找出原因.其实这个问题,本身并不难,好歹给你 ...

随机推荐

  1. Java网络编程之TCP通信

    一.概述 Socket类是Java执行客户端TCP操作的基础类,这个类本身使用代码通过主机操作系统的本地TCP栈进行通信.Socket类的方法会建立和销毁连接,设置各种Socket选项. Server ...

  2. Android studio修改字体(font)大小(size)

    Android Studio 默认编辑器(Editor)的方案(Scheme)是无法修改字体的, 可以Save as, 保存为新的方案(Scheme), 然后更改字体大小; 位置: File-> ...

  3. laravel部署常用命令

    php composer install composer dump-autoload php artisan key:generate .env 及 config/database.php里的数据库 ...

  4. LeetCode 24 Swap Nodes in Pairs （交换相邻节点）

    题目链接: https://leetcode.com/problems/swap-nodes-in-pairs/?tab=Description   Problem: 交换相邻的两个节点     如上 ...

  5. sencha touch 在线实战培训 第一期 第五节

    2014.1.6晚上8点准时开的课 本期培训一共八节,前三堂免费,后面的课程需要付费才可以观看. 本节内容:             实现皮肤自定义样式的修改 css相关理论: 重写官方样式,美化ap ...

  6. 1007: [HNOI2008]水平可见直线[维护下凸壳]

    1007: [HNOI2008]水平可见直线 Time Limit: 1 Sec  Memory Limit: 162 MBSubmit: 7184  Solved: 2741[Submit][Sta ...

  7. 安装Windows Server 2012 R2提示"unable to create a new system partition or locate an existing system partition"解决方法

    重新安装Windows Server 2012 R2,把原来SSD分区全部格式化重建,用U盘启动安装时提示如下: "Setup was unable to create a new syst ...

  8. Cracking the Coding Interview（String and array)

    1.1实现一个算法判断一个字符串是否存在重复字符.如果不能利用另外的数据结构又该如何实现? My solution: /** *利用类似一个hash table的计数 *然后检查这个hash tabl ...

  9. 浅析重定向与反弹Shell命令

    0×01    简介 反弹shell在漏洞证明和利用的过程中都是一个直接有力的手段.由于安全工作或者学习的需要,我们或多或少都会接触到各种反弹shell的命令,于是就有了这个能稍微帮助初学者理解的文档 ...

  10. ElasticSearch概述及Linux下的单机ElasticSearch安装

    原文链接:http://blog.csdn.net/w12345_ww/article/details/52182264 这两天在项目中要涉及到ElasticSearch的使用,就上网去搜索了一些这方 ...