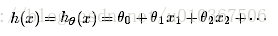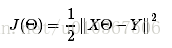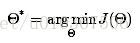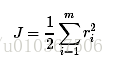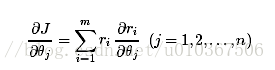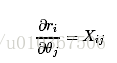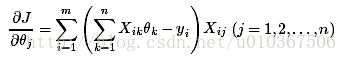梯度下降算法(Gradient Descent)
近期在搞论文,须要用梯度下降算法求解,所以又一次整理分享在这里。
主要包含梯度介绍、公式求导、学习速率选择、代码实现。
梯度下降的性质:
1.求得的解和选取的初始点有关
2.能够保证找到局部最优解,由于梯度终于会减小为0,则步长与梯度的乘积会自己主动越来越小。
梯度简单介绍

问题描写叙述公式求导学习率选择
如果要学习这么一个函数:
那么损失函数能够定义成:
当中X矩阵,每行表示一个数据点,theta是列向量。Y也是列向量。
像这样的优化问题有非常多方法,那咱们先直接求导吧,对于求导过程。好多还是不理解。能够用这样的方法:
首先定义损失变量:
watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvdTAxMDM2NzUwNg==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast" alt="" />
那么损失函数就能够表示成:
一步一步的求导:
再求:
那么把分步骤合起来就是:
能够用最小二乘或者梯度下降来求解,这里我们看看梯度下降的实现,梯度下降的思想不难。仅仅要确定好梯度以及梯度的方向就ok。由于是梯度的反方向去下降,所以在对參数更新的时候要注意:
watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvdTAxMDM2NzUwNg==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast" alt="" />
下降速率能够从0.01開始尝试,越大下降越快,收敛越快。当然下降的速率能够改成自适用的。就是依据梯度的强弱适当调整步伐,这样效果还好一点儿。
代码
clc;
clear
% load data
heart_scale = load('heart_scale');
X = heart_scale.heart_scale_inst;
Y = heart_scale.heart_scale_label;
epsilon = 0.0003;
gamma= 0.0001;
w_old=zeros(size(X,2),1);%參数初始值均设为0
k=1;
figure(1);
while 1
minJ_w(k) = 1/2 * (norm(X*w_old - Y))^2;
w_new = w_old - gamma*(X'*X*w_old - X'*Y);
fprintf('The %dth iteration, minJ_w = %f, \n',k,minJ_w(k));
if norm(w_new-w_old) < epsilon %这里採用两次迭代中优化目标是否变化来判定是否收敛,也能够通过判定优化函数值是否变化来判定是否收敛
W_best = w_new;
break;
end
w_old = w_new;
k=k+1;
end
plot(minJ_w);%观察收敛性梯度下降算法(Gradient Descent)的更多相关文章
- 梯度下降算法(Gradient descent)GD
1.我们之前已经定义了代价函数J,可以将代价函数J最小化的方法,梯度下降是最常用的算法,它不仅仅用在线性回归上,还被应用在机器学习的众多领域中,在后续的课程中,我们将使用梯度下降算法最小化其他函数,而 ...
- 机器学习(1)之梯度下降(gradient descent)
机器学习(1)之梯度下降(gradient descent) 题记:最近零碎的时间都在学习Andrew Ng的machine learning,因此就有了这些笔记. 梯度下降是线性回归的一种(Line ...
- 梯度下降(gradient descent)算法简介
梯度下降法是一个最优化算法,通常也称为最速下降法.最速下降法是求解无约束优化问题最简单和最古老的方法之一,虽然现在已经不具有实用性,但是许多有效算法都是以它为基础进行改进和修正而得到的.最速下降法是用 ...
- 梯度下降(Gradient Descent)小结 -2017.7.20
在求解算法的模型函数时,常用到梯度下降(Gradient Descent)和最小二乘法,下面讨论梯度下降的线性模型(linear model). 1.问题引入 给定一组训练集合(training se ...
- 梯度下降(Gradient descent)
首先,我们继续上一篇文章中的例子,在这里我们增加一个特征,也即卧室数量,如下表格所示: 因为在上一篇中引入了一些符号,所以这里再次补充说明一下: x‘s:在这里是一个二维的向量,例如:x1(i)第i间 ...
- (二)深入梯度下降(Gradient Descent)算法
一直以来都以为自己对一些算法已经理解了,直到最近才发现,梯度下降都理解的不好. 1 问题的引出 对于上篇中讲到的线性回归,先化一个为一个特征θ1,θ0为偏置项,最后列出的误差函数如下图所示: 手动求解 ...
- CS229 2.深入梯度下降(Gradient Descent)算法
1 问题的引出 对于上篇中讲到的线性回归,先化一个为一个特征θ1,θ0为偏置项,最后列出的误差函数如下图所示: 手动求解 目标是优化J(θ1),得到其最小化,下图中的×为y(i),下面给出TrainS ...
- (3)梯度下降法Gradient Descent
梯度下降法 不是一个机器学习算法 是一种基于搜索的最优化方法 作用:最小化一个损失函数 梯度上升法:最大化一个效用函数 举个栗子 直线方程:导数代表斜率 曲线方程:导数代表切线斜率 导数可以代表方向, ...
- <反向传播(backprop)>梯度下降法gradient descent的发展历史与各版本
梯度下降法作为一种反向传播算法最早在上世纪由geoffrey hinton等人提出并被广泛接受.最早GD由很多研究团队各自发表,可他们大多无人问津,而hinton做的研究完整表述了GD方法,同时hin ...
- 梯度下降法Gradient descent(最速下降法Steepest Descent)
最陡下降法(steepest descent method)又称梯度下降法(英语:Gradient descent)是一个一阶最优化算法. 函数值下降最快的方向是什么?沿负梯度方向 d=−gk
随机推荐
- 【转】java文件操作大全
一.获得控制台用户输入的信息 public String getInputMessage() throws IOException...{ System.out.println(&qu ...
- input回车问题
今天有一个问题,就是input对象没有加任何事件自己回车导致跳到了404页面.处理的时候,并发现没找到回车事件的控制. 那么只有一种情况,就是自带的回车控制. 百度了一下,如下面博文里面的写法.我这边 ...
- .NET二级域名共享Session
ASP.NET二级域名站点共享Session状态 今天, 我要写的是如何在二级域名站点之间,主站点和二级域名站点之间共享Session. 首先, Session要共享,站点之间SessionID必须要 ...
- vue案例 - 使用vue实现自定义多选与单选的答题功能
4月底立得flag,五月底插上小旗,结果拖到六月底七月初才来执行.说什么工作忙都是借口,就是睡的比猪早,起的比猪晚. 本来实现多选单选这个功能,vue组件中在表单方面提供了一个v-model指令,非常 ...
- 小程序判断是否授权源码 auth.js
一.auth.js const configGlobal = require('../config/config_global.js'); var util = require('function.j ...
- Java toString()方法的自动调用
如果某一个对象出现在字符串表达式中(涉及“+”字符串对象的表达式),toString()方法就会被自动调动.
- Telnet IMAP Commands Note
http://busylog.net/telnet-imap-commands-note/ Telnet IMAP Commands Note https://www.cnblogs.com/qiu ...
- ogg 12c OGG-01163
数据同步报错: 2017-07-03 12:44:36 ERROR OGG-01163 Oracle GoldenGate Delivery for Oracle, rora_t1.prm: Bad ...
- Jenkins权限管理之Matrix Authorization Strategy
一.权限管理概述 jenkins的权限管理,我目前使用的是Role-based Authorization Strateg.这个很简单,权限是jenkins已经定死了的,就那些.该插件可以让我们新建角 ...
- 【CF799E】Aquarium decoration 线段树
[CF799E]Aquarium decoration 题意:有n个物品,小A和小B各自喜欢其中的某些物品,一件物品可能既被小A喜欢又被小B喜欢,也可能既不被小A喜欢又不被小B喜欢.每个物品都有一个价 ...