POJ 2007 Scrambled Polygon 凸包

Scrambled Polygon

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 7214		Accepted: 3445

Description

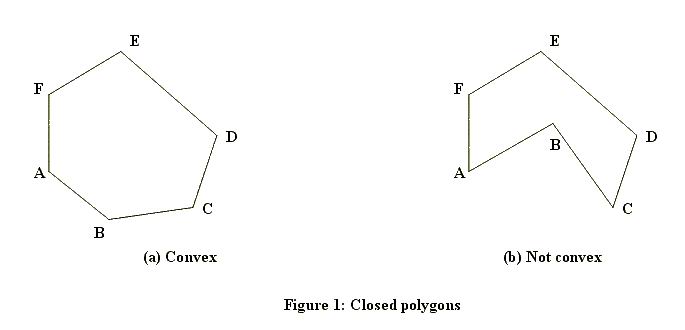
A closed polygon is a figure bounded by a finite number of line segments. The intersections of the bounding line segments are called the vertices of the polygon. When one starts at any vertex of a closed polygon and traverses each bounding line segment exactly once, one comes back to the starting vertex.

A closed polygon is called convex if the line segment joining any two points of the polygon lies in the polygon. Figure 1 shows a closed polygon which is convex and one which is not convex. (Informally, a closed polygon is convex if its border doesn't have any "dents".) 

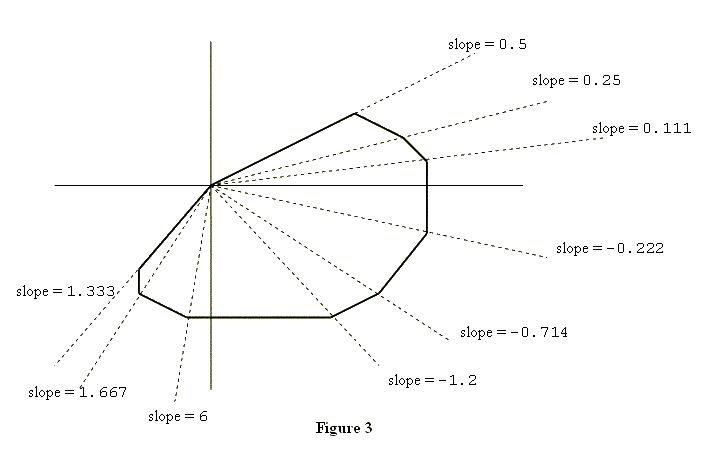
The subject of this problem is a closed convex polygon in the coordinate plane, one of whose vertices is the origin (x = 0, y = 0). Figure 2 shows an example. Such a polygon will have two properties significant for this problem.

The first property is that the vertices of the polygon will be confined to three or fewer of the four quadrants of the coordinate plane. In the example shown in Figure 2, none of the vertices are in the second quadrant (where x < 0, y > 0).

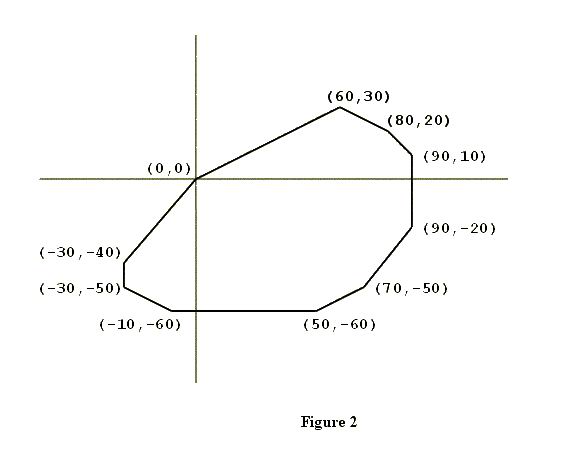
To describe the second property, suppose you "take a trip" around the polygon: start at (0, 0), visit all other vertices exactly once, and arrive at (0, 0). As you visit each vertex (other than (0, 0)), draw the diagonal that connects the current vertex with (0, 0), and calculate the slope of this diagonal. Then, within each quadrant, the slopes of these diagonals will form a decreasing or increasing sequence of numbers, i.e., they will be sorted. Figure 3 illustrates this point. 
 

Input

The input lists the vertices of a closed convex polygon in the plane. The number of lines in the input will be at least three but no more than 50. Each line contains the x and y coordinates of one vertex. Each x and y coordinate is an integer in the range -999..999. The vertex on the first line of the input file will be the origin, i.e., x = 0 and y = 0. Otherwise, the vertices may be in a scrambled order. Except for the origin, no vertex will be on the x-axis or the y-axis. No three vertices are colinear.

Output

The output lists the vertices of the given polygon, one vertex per line. Each vertex from the input appears exactly once in the output. The origin (0,0) is the vertex on the first line of the output. The order of vertices in the output will determine a trip taken along the polygon's border, in the counterclockwise direction. The output format for each vertex is (x,y) as shown below.

Sample Input

0 0
70 -50
60 30
-30 -50
80 20
50 -60
90 -20
-30 -40
-10 -60
90 10

Sample Output

(0,0)
(-30,-40)
(-30,-50)
(-10,-60)
(50,-60)
(70,-50)
(90,-20)
(90,10)
(80,20)
(60,30)

题目叙述很长，其实就是给出一组包括原点在内的点，求出这组点的凸包的各个定点，按照逆时针方向从原点开始输出整个凸包的顶点
两种方法可以做：一个是Graham-Scan，还有就是直接极坐标排序，选取原点为基准点来排
代码如下

/*极坐标排序方法*/
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>
#define EPS 1e-8

using namespace std;
struct point{
    double x, y;
};
const int maxn = ;
point p[maxn], pp;//pp是基准点
int n;
int sgn(double x)
{
    if (fabs(x) < EPS)
        return ;
    return x <  ? - : ;
}
double get_direction(point p1, point p2, point p3)
{
    return ((p3.x - p1.x) * (p2.y - p1.y) - (p2.x - p1.x) * (p3.y - p1.y));
}
double get_distance(point p1, point p2)
{
    return sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
}
bool cmp(const point p1, const point p2)//极坐标排序的比较函数
{
    if (sgn(get_direction(pp, p1, p2)) < )
        return true;
    if (sgn(get_direction(pp, p1, p2)) ==  && get_distance(pp, p1) < get_distance(pp, p2))
        return true;
    return false;
}
int main()
{
    n = ;
    while (~scanf("%lf %lf", &p[n].x, &p[n].y))
        n++;
    int i;
    for (i = ; i < n; i++)
    {
        if (p[i].x ==  && p[i].y == )
            break;
    }
    pp = p[i];
    p[i] = p[];
    p[] = pp;

    sort(p, p + n, cmp);
    for (int i = ; i < n; i++)
        printf("(%.0f,%.0f)\n", p[i].x, p[i].y);

    return ;
}

普通的Graham

/*************************************************************************
    > File Name:            poj_2007.cpp
    > Author:               Howe_Young
    > Mail:                 1013410795@qq.com
    > Created Time:         2015年04月16日 星期四 14时47分43秒
 ************************************************************************/

#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <algorithm>
#include <cstdio>
#define EPS 1e-8
using namespace std;
struct point{
    double x, y;
};
const int maxn = ;
point p[maxn];
int n, top, convex[maxn];
int sgn(double x)
{
    if (fabs(x) < EPS)
        return ;
    return x <  ? - : ;
}
bool cmp(const point p1, const point p2)
{
    return ((p1.y == p2.y && p1.x < p2.x) || p1.y < p2.y);
}
double get_direction(point p1, point p2, point p3)
{
    return ((p3.x - p1.x) * (p2.y - p1.y) - (p2.x - p1.x) * (p3.y - p1.y));
}
void Graham()
{
    top = ;
    for (int i = ; i < n; i++)
    {
        while (top >  && sgn(get_direction(p[convex[top - ]], p[convex[top - ]], p[i])) >= )
            top--;
        convex[top++] = i;
    }
    int tmp = top;
    for (int i = n - ; i >= ; i--)
    {
        while (top > tmp && sgn(get_direction(p[convex[top - ]], p[convex[top - ]], p[i])) >= )
            top--;
        convex[top++] = i;
    }
}
int main()
{
    n = ;
    while (~scanf("%lf %lf", &p[n].x,  &p[n].y)) n++;
    sort(p, p + n, cmp);
    Graham();
    int k;
    for (k = ; k < top; k++)
        if (p[convex[k]].x ==  && p[convex[k]].y == )
            break;
    for (int i = k; i < top - ; i++)
        printf("(%.0f,%.0f)\n", p[convex[i]].x, p[convex[i]].y);
    for (int i = ; i < k; i++)
        printf("(%.0f,%.0f)\n", p[convex[i]].x, p[convex[i]].y);
    return ;
}