leecode 每日解题思路 127-Factorial Trailing Zeroes

原题描述：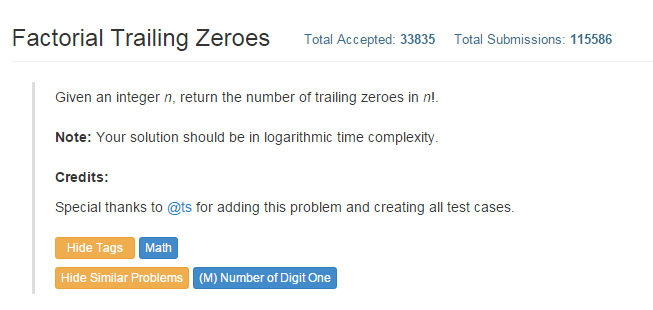

原题地址： Factorial Trailing Zeroes

题目描述很直接， 给出一个整数N, 求这个N的阶乘后尾有几个零。（要求O(logN)时间复杂度）

个人思路：

　　一开始，最简单的思维就是直接求要知道， n!的增长速度， 比O(n^2)还要大， 对于32位整型来说， 当N=13的时候， 数据就已经开始溢出了，

　　

　　好吧， 就算使用long型也是到N=21时，表示数位也不够用了，

      

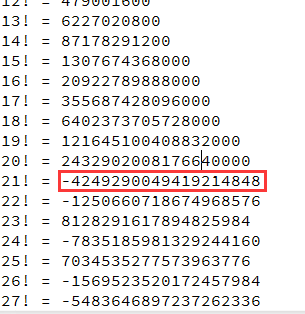
　　那么， 这条路其实是走不通的， （就算考虑使用大数阶乘解决方案， 但这背离了这道题目的初衷，而且也达不到O(logN)的时间复杂度要求）：

到这里， 我们先想想，1~10这十个数字，那些数相乘后有末尾零，也就是10的倍数？，显而易见的，只有碰到任意的偶数与5的倍数相乘是，才有得

才会多出一个零。 从而， 我们这边5的倍数这个元素就是关键点。

　　其实，到了上一步，这个问题已经解决掉一半了， 剩下的工作就是求取给出的1~N个数里， 存在几个5的倍数， done!

　　当时我就觉得问题已经解决，而且时间复杂度只有O(1)呢 : )

　　

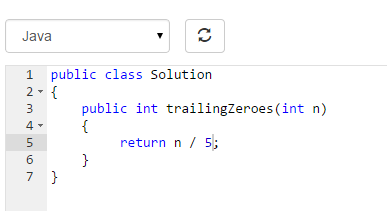
　　马上提交， 结果呵呵：Wrong Anwser

　　

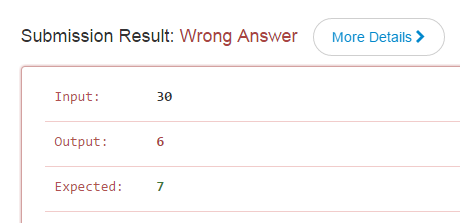
　　但是觉得30里不就6个5的倍数么， 得到的数尾应该就是6个零才对啊，然后我仔细盯着着这6个数：

　　

　　机智的朋友们应该一经发现了， 可是我却呆了一会才发现， 老子当时就是一拍大腿: "卧槽， 还有一种情况没有考虑!"

　　

　　没错， 就是这个罪魁祸首， 虽然他也是5的倍数， 但是他是5的n次数（包括其倍数， 例如25*4 = 100,100/10 = 10, 还是5的倍数，就是这种情况没考虑）， 也就是意味他需要n次消化掉才不会有,  既然还要考虑到5的n次， 那么， 每次每隔5一次数， 然后再在结果中隔5取一次数， done!

　　

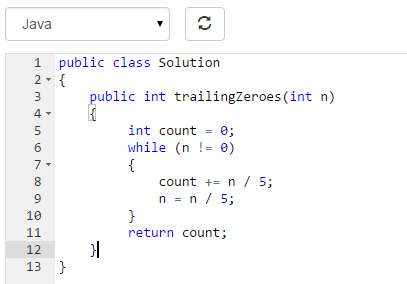
　　这次也是果断提交（时间复杂度 O(log(N)), 底数为5， 肯定比默认底数为2来的更快。）：duang!

　　另外， 关于执行速度， 貌似用C的话， 递归反而是最快的， 我估计是测试用例的问题吧， 反正不在今天的讨论范围,有兴趣的同学自己研究下,或者在评论区指教下，谢谢！