【NOIP 2012 开车旅行】***

题目描述

小 A 和小 B 决定利用假期外出旅行，他们将想去的城市从 1 到 N 编号，且编号较小的

城市在编号较大的城市的西边，已知各个城市的海拔高度互不相同，记城市 i 的海拔高度为

Hi，城市 i 和城市 j 之间的距离 d[i,j]恰好是这两个城市海拔高度之差的绝对值，即

d[i,j] = |Hi− Hj|。

旅行过程中，小 A 和小 B 轮流开车，第一天小 A 开车，之后每天轮换一次。他们计划

选择一个城市 S 作为起点，一直向东行驶，并且最多行驶 X 公里就结束旅行。小 A 和小 B

的驾驶风格不同，小 B 总是沿着前进方向选择一个最近的城市作为目的地，而小 A 总是沿

着前进方向选择第二近的城市作为目的地（注意：本题中如果当前城市到两个城市的距离

相同，则认为离海拔低的那个城市更近）。如果其中任何一人无法按照自己的原则选择目的

城市，或者到达目的地会使行驶的总距离超出 X 公里，他们就会结束旅行。

在启程之前，小 A 想知道两个问题：

1．对于一个给定的 X=X0，从哪一个城市出发，小 A 开车行驶的路程总数与小 B 行驶

的路程总数的比值最小（如果小 B 的行驶路程为 0，此时的比值可视为无穷大，且两个无穷大视为相等）。如果从多个城市出发，小 A 开车行驶的路程总数与小 B 行驶的路程总数的比

值都最小，则输出海拔最高的那个城市。

1. 对任意给定的 X=Xi和出发城市 Si，小 A 开车行驶的路程总数以及小 B 行驶的路程

总数。

输入输出格式

输入格式：

第一行包含一个整数 N，表示城市的数目。

第二行有 N 个整数，每两个整数之间用一个空格隔开，依次表示城市 1 到城市 N 的海

拔高度，即 H1，H2，……，Hn，且每个 Hi都是不同的。

第三行包含一个整数 X0。

第四行为一个整数 M，表示给定 M 组 Si和 Xi。

接下来的 M 行，每行包含 2 个整数 Si和 Xi，表示从城市 Si出发，最多行驶 Xi公里。

输出格式：

输出共 M+1 行。

第一行包含一个整数 S0，表示对于给定的 X0，从编号为 S0的城市出发，小 A 开车行驶

的路程总数与小 B 行驶的路程总数的比值最小。

接下来的 M 行，每行包含 2 个整数，之间用一个空格隔开，依次表示在给定的 Si和

Xi下小 A 行驶的里程总数和小 B 行驶的里程总数。

输入输出样例

输入样例#1：

drive1
4
2 3 1 4
3
4
1 3
2 3
3 3
4 3

drive2
 10
4 5 6 1 2 3 7 8 9 10
7
10
1 7
2 7
3 7
4 7
5 7
6 7
7 7
8 7
9 7
10 7

输出样例#1：

drive1
1
1 1
2 0
0 0
0 0 

drive2
2
3 2
2 4
2 1
2 4
5 1
5 1
2 1
2 0
0 0
0 0

说明

【输入输出样例 1 说明】

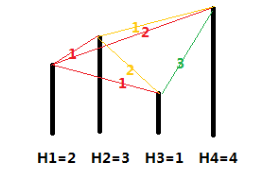
各个城市的海拔高度以及两个城市间的距离如上图所示。

如果从城市 1 出发，可以到达的城市为 2,3,4，这几个城市与城市 1 的距离分别为 1,1,2，

但是由于城市 3 的海拔高度低于城市 2，所以我们认为城市 3 离城市 1 最近，城市 2 离城市

1 第二近，所以小 A 会走到城市 2。到达城市 2 后，前面可以到达的城市为 3,4，这两个城

市与城市 2 的距离分别为 2,1，所以城市 4 离城市 2 最近，因此小 B 会走到城市 4。到达城

市 4 后，前面已没有可到达的城市，所以旅行结束。

如果从城市 2 出发，可以到达的城市为 3,4，这两个城市与城市 2 的距离分别为 2,1，由

于城市 3 离城市 2 第二近，所以小 A 会走到城市 3。到达城市 3 后，前面尚未旅行的城市为

4，所以城市 4 离城市 3 最近，但是如果要到达城市 4，则总路程为 2+3=5>3，所以小 B 会

直接在城市 3 结束旅行。

如果从城市 3 出发，可以到达的城市为 4，由于没有离城市 3 第二近的城市，因此旅行

还未开始就结束了。

如果从城市 4 出发，没有可以到达的城市，因此旅行还未开始就结束了。

【输入输出样例 2 说明】

当 X=7 时，

如果从城市 1 出发，则路线为 1 -> 2 -> 3 -> 8 -> 9，小 A 走的距离为 1+2=3，小 B 走的

距离为 1+1=2。（在城市 1 时，距离小 A 最近的城市是 2 和 6，但是城市 2 的海拔更高，视

为与城市 1 第二近的城市，所以小 A 最终选择城市 2；走到 9 后，小 A 只有城市 10 可以走，

没有第 2 选择可以选，所以没法做出选择，结束旅行）

如果从城市 2 出发，则路线为 2 -> 6 -> 7 ，小 A 和小 B 走的距离分别为 2，4。

如果从城市 3 出发，则路线为 3 -> 8 -> 9，小 A 和小 B 走的距离分别为 2，1。

如果从城市 4 出发，则路线为 4 -> 6 -> 7，小 A 和小 B 走的距离分别为 2，4。

如果从城市 5 出发，则路线为 5 -> 7 -> 8 ，小 A 和小 B 走的距离分别为 5，1。

如果从城市 6 出发，则路线为 6 -> 8 -> 9，小 A 和小 B 走的距离分别为 5，1。

如果从城市 7 出发，则路线为 7 -> 9 -> 10，小 A 和小 B 走的距离分别为 2，1。

如果从城市 8 出发，则路线为 8 -> 10，小 A 和小 B 走的距离分别为 2，0。

全国信息学奥林匹克联赛（NOIP2012）复赛

提高组 day1

第 7 页 共 7 页

如果从城市 9 出发，则路线为 9，小 A 和小 B 走的距离分别为 0，0（旅行一开始就结

束了）。

如果从城市 10 出发，则路线为 10，小 A 和小 B 走的距离分别为 0，0。

从城市 2 或者城市 4 出发小 A 行驶的路程总数与小 B 行驶的路程总数的比值都最小，

但是城市 2 的海拔更高，所以输出第一行为 2。

【数据范围】

对于 30%的数据，有 1≤N≤20，1≤M≤20；

对于 40%的数据，有 1≤N≤100，1≤M≤100；

对于 50%的数据，有 1≤N≤100，1≤M≤1,000；

对于 70%的数据，有 1≤N≤1,000，1≤M≤10,000；

对于100%的数据，有1≤N≤100,000，1≤M≤10,000，-1,000,000,000≤Hi≤1,000,000,000，

0≤X0≤1,000,000,000，1≤Si≤N，0≤Xi≤1,000,000,000，数据保证 Hi互不相同。

NOIP 2012 提高组 第一天 第三题

%%%%%%奥爷爷

【其实我几乎是抄代码的ORZ。。。奥爷爷的代码太美了ORZ。。。

一开始看错题了ORZ【是总距离

总距离的话就容易想到是倍增【有个很猥琐的地方是它是轮流开车的【但是2^i(i>0)都是偶数嘛orz= =【就是说走了一截还是那个人先走

然后前面预处理的地方= =额= =一开始还打set。。。其实双向链表就好【我竟然没想到，我可是链表的小粉丝啊ORZ= =

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<queue>
 #include<cmath>
 using namespace std;
 #define Maxn 100010
 #define Maxd 20
 #define LL long long

 LL myabs(LL x) {return x>?x:-x;}

 LL h[Maxn],id[Maxn];
 LL lt[Maxn],nt[Maxn];

 bool cmp(LL x,LL y)
 {
     return (h[x]==h[y])?(x<y):(h[x]<h[y]);
 }

 LL now;
 bool cmp2(LL x,LL y)
 {
     if(myabs(h[x]-h[now])==myabs(h[y]-h[now])) return h[x]<h[y];
     return myabs(h[x]-h[now])<myabs(h[y]-h[now]);
 }

 LL s1[Maxn][Maxd],s2[Maxn][Maxd];
 LL f[Maxn][Maxd];
 LL nr[Maxn],n;

 void init()
 {
     scanf("%lld",&n);
     for(LL i=;i<=n;i++) scanf("%lld",&h[i]);
     for(LL i=;i<=n;i++) id[i]=i;
     sort(id+,id++n,cmp);
     memset(nt,,sizeof(nt));
     memset(lt,,sizeof(lt));
     for(LL i=;i<n;i++)
     {
         nt[id[i]]=id[i+];
         lt[id[i+]]=id[i];
     }
     for(LL i=;i<=n;i++)
     {
         id[]=;
         if(nt[i]) id[++id[]]=nt[i];
         if(nt[nt[i]]) id[++id[]]=nt[nt[i]];
         if(lt[i]) id[++id[]]=lt[i];
         if(lt[lt[i]]) id[++id[]]=lt[lt[i]];
         now=i;
         sort(id+,id++id[],cmp2);
         if(id[]>=) nr[i]=id[];
         if(id[]>=) f[i][]=id[],s1[i][]=myabs(h[id[]]-h[i]);
         if(lt[i]) nt[lt[i]]=nt[i];
         if(nt[i]) lt[nt[i]]=lt[i];
     }
     for(LL i=;i<=n;i++)
     {
         f[i][]=nr[f[i][]];
         s1[i][]=s1[i][];
         s2[i][]=myabs(h[f[i][]]-h[nr[f[i][]]]);
     }
     for(LL j=;j<=;j++)
      for(LL i=;i<=n;i++)
      {
        f[i][j]=f[f[i][j-]][j-];
        s1[i][j]=s1[i][j-]+s1[f[i][j-]][j-];
        s2[i][j]=s2[i][j-]+s2[f[i][j-]][j-];
      }
 }

 LL a1,a2;

 void get_ans(LL ss,LL xx)
 {
     a1=;a2=;LL sum=;
     for(LL i=;i>=;i--)
     {
         if(f[ss][i]&&sum+s1[ss][i]+s2[ss][i]<=xx)
         {
             a1+=s1[ss][i];
             a2+=s2[ss][i];
             sum+=s1[ss][i]+s2[ss][i];
             ss=f[ss][i];
         }
     }
 }

 void ffind()
 {
     LL x0,A=,B=;
     now=;h[]=;
     scanf("%lld",&x0);
     for(LL i=;i<=n;i++)
     {
         get_ans(i,x0);
         if(B!=&&a2!=&&((A*a2>a1*B)||(A*a2==a1*B&&h[i]>h[now]))) A=a1,B=a2,now=i;
         else if(B==&&((a2==&&h[i]>h[now])||a2!=)) A=a1,B=a2,now=i;
     }
     printf("%lld\n",now);
     LL q;
     scanf("%lld",&q);
     for(LL i=;i<=q;i++)
     {
         LL ss,xx;
         scanf("%lld%lld",&ss,&xx);
         get_ans(ss,xx);
         printf("%lld %lld\n",a1,a2);
     }
 }

 int main()
 {
     init();
     ffind();
     return ;
 }

2016-11-16 15:55:40