Arrays.sort() ----- DualPivotQuicksort

Arrays.sort() ----- DualPivotQuicksort

DualPivotQuicksort是Arrays.sort()对基本类型的排序算法，它不止使用了双轴快速排序，还使用了TimSort、插入排序、成对插入排序、3-way快速排序。

算法介绍

成对插入排序

具体执行过程：

1. 将要插入的数据，第一个值赋值a1,第二个值赋值a2
2. 然后判断a1与a2的大小，使a1要大于a2
3. 接下来，首先是插入大的数值a1，将a1与k之前的数字一一比较，直到数值小于a1为止，把a1插入到合适的位置，注意：比a1大的值右移2位
4. 接下来，插入小的数值a2,将a2与此时k之前的数字一一比较，直到数值小于a2为止，将a2插入到合适的位置，注意：比a2大的值右移1位
5. 最后把最后一个没有遍历到的数据插入到合适位置

3-way快速排序

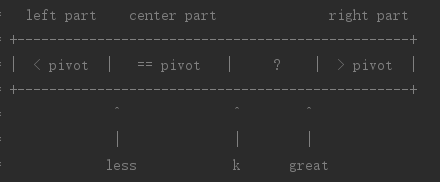
具体执行过程：

1. a[k] < pivot 交换a[less]和a[k]，然后less和k都自增1，k继续扫描
2. a[k] = pivot k自增1，k接着继续扫描
3. a[k] > pivot 交换a[great]和a[k],但是我们不能直接将a[k]与a[great]交换，因为目前a[great]和pivot的关系未知，所以我们这个时候应该从great的位置自右向左扫描。而a[great]与pivot的关系可以继续分为三种情况讨论:
   1. a[great] > pivot great自减1，great接着继续扫描
   2. a[great] == pivot 交换a[k]和a[great]，k自增1，great自减1，k继续扫描（注意此时great的扫描就结束了）
   3. a[great] < pivot: 此时我们注意到a[great] < pivot, a[k] > pivot, a[less] == pivot，那么我们只需要将a[great]放到a[less]上，a[k]放到a[great]上，而a[less]放到a[k]上。然后less和k自增1，great自减1，k继续扫描（注意此时great的扫描就结束了）

双轴快速排序

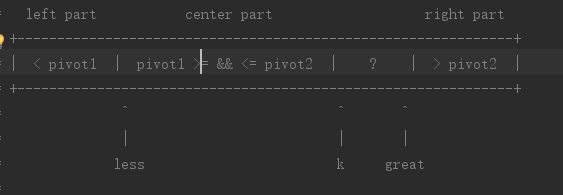
具体执行过程：

1. a[k] < pivot1 less先自增，交换a[less]和a[k]，k自增1，k接着继续扫描
2. a[k] >= pivot1 && a[k] <= pivot2 k自增1，k接着继续扫描
3. a[k] > pivot2: 这个时候显然a[k]应该放到最右端大于pivot2的部分。但此时，我们不能直接将a[k]与a[great]交换,因为目前a[great]和pivot1以及pivot2的关系未知，所以我们这个时候应该从great自右向左扫描。而a[great]与pivot1和pivot2的关系可以继续分为三种情况讨论
   1. a[great] > pivot2 j接着继续扫描
   2. a[great] >= pivot1且a[great] <= pivot2 交换a[k]和a[great]，great自减1，k自增1，k继续扫描（注意此时great的扫描就结束了）
   3. a[great] < pivot1 先将i自增1，此时我们注意到a[great] < pivot1, a[k] > pivot2, pivot1 <= a[less] <=pivot2，那么我们只需要将a[great]放到a[less]上，a[k]放到a[great]上，而a[less]放到a[k]上。k自增1，great自减1，然后k继续扫描（此时great的扫描就结束了）

注意

1. pivot1和pivot2在始终不参与k，greate扫描过程。
2. 扫描结束时，a[less-1]表示了小于pivot1部分的最后一个元素，A[greate+1]表示了大于pivot2的第一个元素，这时我们只需要交换pivot1（即A[L]）和A[less-1]，交换pivot2（即A[R]）与A[greate+1]，同时我们可以确定A[less-1]和A[greate+1]所在的位置在后续的排序过程中不会发生变化（这一步非常重要，否则可能引起无限递归导致的栈溢出），最后我们只需要对A[L, less-2]，A[less, great]，A[great+1, R]这三个部分继续递归上述操作即可。

TimSort

TimSort可以看另一篇文章：Arrays.sort() ----- TimSort

jdk1.8源码

static void sort(int[] a, int left, int right,
                 int[] work, int workBase, int workLen) {
    // Use Quicksort on small arrays
    if (right - left < QUICKSORT_THRESHOLD) {
        sort(a, left, right, true);
        return;
    }
	//大于阈值使用阉割版的TimSort，去掉了自适应
	........

}

private static void sort(int[] a, int left, int right, boolean leftmost) {
    int length = right - left + 1;

    // 小于一个阈值的使用插入排序
    if (length < INSERTION_SORT_THRESHOLD) {
        if (leftmost) {//位于整个数组最左边，使用传统插入排序
            for (int i = left, j = i; i < right; j = ++i) {
                int ai = a[i + 1];
                while (ai < a[j]) {
                    a[j + 1] = a[j];
                    if (j-- == left) {
                        break;
                    }
                }
                a[j + 1] = ai;
            }
        } else {//成对插入排序
            /*
             * 跳过左边已排序的部分
             */
            do {
                if (left >= right) {
                    return;
                }
            } while (a[++left] >= a[left - 1]);

            /*
             * Every element from adjoining part plays the role
             * of sentinel, therefore this allows us to avoid the
             * left range check on each iteration. Moreover, we use
             * the more optimized algorithm, so called pair insertion
             * sort, which is faster (in the context of Quicksort)
             * than traditional implementation of insertion sort.
             */
            for (int k = left; ++left <= right; k = ++left) {
                int a1 = a[k], a2 = a[left];

                if (a1 < a2) {
                    a2 = a1; a1 = a[left];
                }
                while (a1 < a[--k]) {
                    a[k + 2] = a[k];
                }
                a[++k + 1] = a1;

                while (a2 < a[--k]) {
                    a[k + 1] = a[k];
                }
                a[k + 1] = a2;
            }
            int last = a[right];

            while (last < a[--right]) {
                a[right + 1] = a[right];
            }
            a[right + 1] = last;
        }
        return;
    }

    // Inexpensive approximation of length / 7
    int seventh = (length >> 3) + (length >> 6) + 1;

    /*
     * Sort five evenly spaced elements around (and including) the
     * center element in the range. These elements will be used for
     * pivot selection as described below. The choice for spacing
     * these elements was empirically determined to work well on
     * a wide variety of inputs.
     */
    int e3 = (left + right) >>> 1; // The midpoint
    int e2 = e3 - seventh;
    int e1 = e2 - seventh;
    int e4 = e3 + seventh;
    int e5 = e4 + seventh;

    // Sort these elements using insertion sort
    if (a[e2] < a[e1]) { int t = a[e2]; a[e2] = a[e1]; a[e1] = t; }

    if (a[e3] < a[e2]) { int t = a[e3]; a[e3] = a[e2]; a[e2] = t;
        if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; }
    }
    if (a[e4] < a[e3]) { int t = a[e4]; a[e4] = a[e3]; a[e3] = t;
        if (t < a[e2]) { a[e3] = a[e2]; a[e2] = t;
            if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; }
        }
    }
    if (a[e5] < a[e4]) { int t = a[e5]; a[e5] = a[e4]; a[e4] = t;
        if (t < a[e3]) { a[e4] = a[e3]; a[e3] = t;
            if (t < a[e2]) { a[e3] = a[e2]; a[e2] = t;
                if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; }
            }
        }
    }

    // Pointers
    int less  = left;  // The index of the first element of center part
    int great = right; // The index before the first element of right part

    if (a[e1] != a[e2] && a[e2] != a[e3] && a[e3] != a[e4] && a[e4] != a[e5]) {//双轴快速排序
        /*
         * Use the second and fourth of the five sorted elements as pivots.
         * These values are inexpensive approximations of the first and
         * second terciles of the array. Note that pivot1 <= pivot2.
         */
        int pivot1 = a[e2];
        int pivot2 = a[e4];

        /*
         * The first and the last elements to be sorted are moved to the
         * locations formerly occupied by the pivots. When partitioning
         * is complete, the pivots are swapped back into their final
         * positions, and excluded from subsequent sorting.
         */
        a[e2] = a[left];
        a[e4] = a[right];

        /*
         * Skip elements, which are less or greater than pivot values.
         */
        while (a[++less] < pivot1);
        while (a[--great] > pivot2);

        /*
         * Partitioning:
         *
         *   left part           center part                   right part
         * +--------------------------------------------------------------+
         * |  < pivot1  |  pivot1 <= && <= pivot2  |    ?    |  > pivot2  |
         * +--------------------------------------------------------------+
         *               ^                          ^       ^
         *               |                          |       |
         *              less                        k     great
         *
         * Invariants:
         *
         *              all in (left, less)   < pivot1
         *    pivot1 <= all in [less, k)     <= pivot2
         *              all in (great, right) > pivot2
         *
         * Pointer k is the first index of ?-part.
         */
        outer:
        for (int k = less - 1; ++k <= great; ) {
            int ak = a[k];
            if (ak < pivot1) { // Move a[k] to left part
                a[k] = a[less];
                /*
                 * Here and below we use "a[i] = b; i++;" instead
                 * of "a[i++] = b;" due to performance issue.
                 */
                a[less] = ak;
                ++less;
            } else if (ak > pivot2) { // Move a[k] to right part
                while (a[great] > pivot2) {
                    if (great-- == k) {
                        break outer;
                    }
                }
                if (a[great] < pivot1) { // a[great] <= pivot2
                    a[k] = a[less];
                    a[less] = a[great];
                    ++less;
                } else { // pivot1 <= a[great] <= pivot2
                    a[k] = a[great];
                }
                /*
                 * Here and below we use "a[i] = b; i--;" instead
                 * of "a[i--] = b;" due to performance issue.
                 */
                a[great] = ak;
                --great;
            }
        }

        // Swap pivots into their final positions
        a[left]  = a[less  - 1]; a[less  - 1] = pivot1;
        a[right] = a[great + 1]; a[great + 1] = pivot2;

        // Sort left and right parts recursively, excluding known pivots
        sort(a, left, less - 2, leftmost);
        sort(a, great + 2, right, false);

		//如果中间区域太大，使用双轴的思想，优化中间区域
        if (less < e1 && e5 < great) {
            /*
             * Skip elements, which are equal to pivot values.
             */
            while (a[less] == pivot1) {
                ++less;
            }

            while (a[great] == pivot2) {
                --great;
            }

            /*
             * Partitioning:
             *
             *   left part         center part                  right part
             * +----------------------------------------------------------+
             * | == pivot1 |  pivot1 < && < pivot2  |    ?    | == pivot2 |
             * +----------------------------------------------------------+
             *              ^                        ^       ^
             *              |                        |       |
             *             less                      k     great
             *
             * Invariants:
             *
             *              all in (*,  less) == pivot1
             *     pivot1 < all in [less,  k)  < pivot2
             *              all in (great, *) == pivot2
             *
             * Pointer k is the first index of ?-part.
             */
            outer:
            for (int k = less - 1; ++k <= great; ) {
                int ak = a[k];
                if (ak == pivot1) { // Move a[k] to left part
                    a[k] = a[less];
                    a[less] = ak;
                    ++less;
                } else if (ak == pivot2) { // Move a[k] to right part
                    while (a[great] == pivot2) {
                        if (great-- == k) {
                            break outer;
                        }
                    }
                    if (a[great] == pivot1) { // a[great] < pivot2
                        a[k] = a[less];
                        /*
                         * Even though a[great] equals to pivot1, the
                         * assignment a[less] = pivot1 may be incorrect,
                         * if a[great] and pivot1 are floating-point zeros
                         * of different signs. Therefore in float and
                         * double sorting methods we have to use more
                         * accurate assignment a[less] = a[great].
                         */
                        a[less] = pivot1;
                        ++less;
                    } else { // pivot1 < a[great] < pivot2
                        a[k] = a[great];
                    }
                    a[great] = ak;
                    --great;
                }
            }
        }

        // Sort center part recursively
        sort(a, less, great, false);

    } else { //使用3-ways快速排序
        /*
         * Use the third of the five sorted elements as pivot.
         * This value is inexpensive approximation of the median.
         */
        int pivot = a[e3];

        /*
         * Partitioning degenerates to the traditional 3-way
         * (or "Dutch National Flag") schema:
         *
         *   left part    center part              right part
         * +-------------------------------------------------+
         * |  < pivot  |   == pivot   |     ?    |  > pivot  |
         * +-------------------------------------------------+
         *              ^              ^        ^
         *              |              |        |
         *             less            k      great
         *
         * Invariants:
         *
         *   all in (left, less)   < pivot
         *   all in [less, k)     == pivot
         *   all in (great, right) > pivot
         *
         * Pointer k is the first index of ?-part.
         */
        for (int k = less; k <= great; ++k) {
            if (a[k] == pivot) {
                continue;
            }
            int ak = a[k];
            if (ak < pivot) { // Move a[k] to left part
                a[k] = a[less];
                a[less] = ak;
                ++less;
            } else { // a[k] > pivot - Move a[k] to right part
                while (a[great] > pivot) {
                    --great;
                }
                if (a[great] < pivot) { // a[great] <= pivot
                    a[k] = a[less];
                    a[less] = a[great];
                    ++less;
                } else { // a[great] == pivot
                    /*
                     * Even though a[great] equals to pivot, the
                     * assignment a[k] = pivot may be incorrect,
                     * if a[great] and pivot are floating-point
                     * zeros of different signs. Therefore in float
                     * and double sorting methods we have to use
                     * more accurate assignment a[k] = a[great].
                     */
                    a[k] = pivot;
                }
                a[great] = ak;
                --great;
            }
        }

        /*
         * Sort left and right parts recursively.
         * All elements from center part are equal
         * and, therefore, already sorted.
         */
        sort(a, left, less - 1, leftmost);
        sort(a, great + 1, right, false);
    }
}

参考资料

https://www.cnblogs.com/nullzx/p/5880191.html

https://www.jianshu.com/p/6d26d525bb96