[学习笔记] Treap

想必大家都知道一种叫做二叉搜索树这东西吧，那么我们知道，在某些特殊情况下，二叉搜索树会退化成一条链，而且如果出题人成心想卡你的话也很简单，分分钟把你(n log n)的期望卡成。那么我们该如何避免这种尴尬状况的出现呢？我们的范浩强大佬就创造了一种名为Treap的算法。

那么这个算法是如何实现的呢？

首先，我们发现：

当我们将一组数放入一棵二叉搜索树的顺序改变时，那么你最终得到的二叉搜索树也会发生变化。

这便是Treap算法优化二叉搜索树的突破口。这二叉搜索树的这一个特点也就意味着我们完全可以将一棵已经退化成一条链的二叉搜索树优化成一个两边相对平衡的二叉搜索树。

在这里，我隆重介绍一种在一颗二叉搜索树中可谓BUG级别的操作——左/右旋。

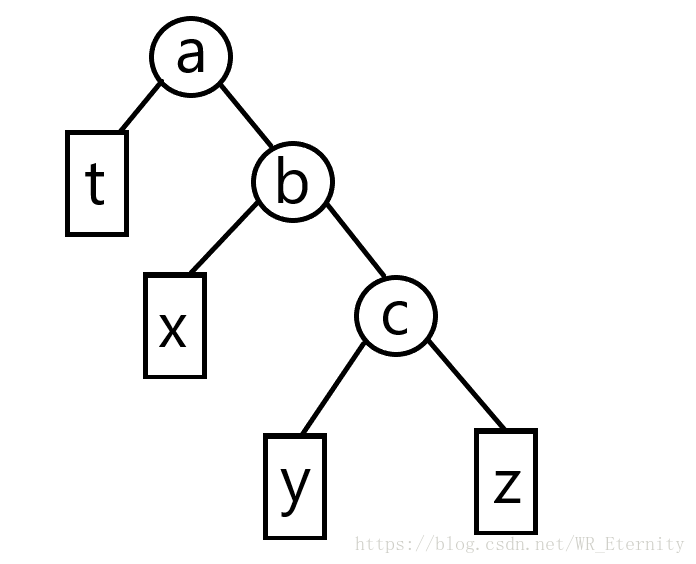
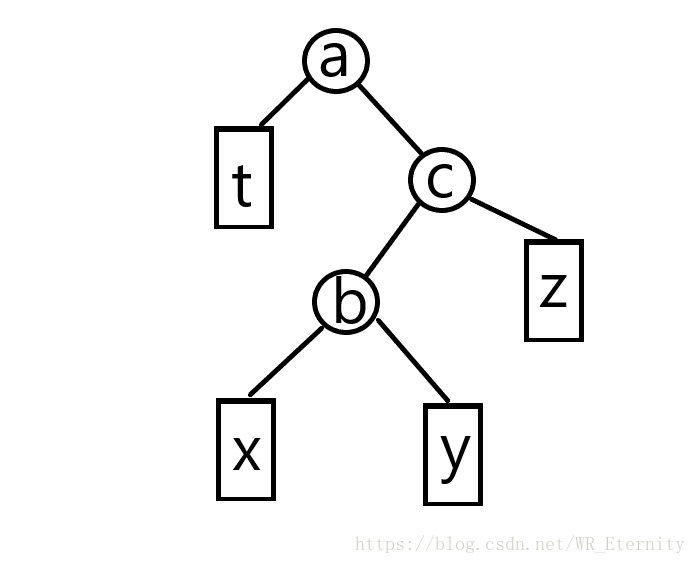
这个操作可以在满足一颗二叉搜索树性质的同时交换父亲与儿子的位置，也就是说这个操作可以逆天到让爸爸给他儿子当儿子，儿子当爸爸，而且还是被法律所允许的！！！（想想就恐(ji)怖(dong)）嗯，具体操作如下图：

a，b，c分别为三个节点，其中我们要交换的是b节点和c节点。t为a的整颗左子树，x为b的整颗左子树，y为c的整颗左子树，z为c的整颗右子树。可以看见，右图由左图左旋得到，而左图就是由右图右旋得到的。

学会了这个操作也就意味这我们可以对这颗二叉搜索树为所欲为了！

所以我们现在所要考虑的就是如何做到让其相对平衡？

其实答案很简单，就是给每个数随机一个第二关键字，并且在满足一颗二叉搜索树性质的同时，用堆来维护这个第二关键字（我这里采用了大根堆），然后我们便能够得到一颗相对平衡的二叉搜索树了！

这也便是Treap这个名字的由来：Tree（树）+Heap（堆）

1、废话不多说，先给大家附上我的变量定义

type
    treap=record
        key,fix,cnt,siz:longint;
        ch:array[0..1]of longint;

//ch数组表示它连接的儿子节点ch[-1]为左儿子，ch[1]为右儿子（这么定义就是为了偷懒。。。）
//key为第一关键字（就是它的数值）fix为第二关键字（我们随机出来的）
//cnt表示与当前节点数值相同的点的个数，size表示以他为根的子树的大小
//father为它的父亲节点
//注意，因为旋转操作是涉及到祖孙三代的，所以既要记录儿子又要记录父亲。

end; 

2、逆天的旋转操作

procedure rotate(var x:longint;d:longint);
var
    son:longint;
begin
    son:=t[x].ch[d];
    t[x].ch[d]:=t[son].ch[1-d];
    t[son].ch[1-d]:=x;
    update(x); update(son);
    x:=son;
end;

3、更新操作

procedure update(x:longint);
begin
    t[x].siz:=t[x].cnt+t[t[x].ch[0]].siz+t[t[x].ch[1]].siz;
end;

4、插入操作

删除操作分为三步：

1、找到该数在Treap中的位置，并将路径上的点size域+1；

2、插入该数，若树中已有该数，则将该数的cnt域+1，否则就新建一个叶子节点；

3、回溯时，判断儿子和父亲的fix（第二关键字）域是否满足堆的性质，若不满足则用旋转操作把父亲结点旋下来，将儿子节点转上去，使其继续满足堆的性质；

procedure inset(var k:longint;key:longint);
var
    d:longint;
begin
    if k=0 then
    begin
        inc(cnt); k:=cnt;                              //新建节点
        t[k].key:=key; t[k].fix:=random(100000000);
        t[k].cnt:=1; t[k].siz:=1;
        exit;
    end else inc(t[k].siz);                            //路径上经过的siz都加1
    if t[k].key=key then begin inc(t[k].cnt); exit; end;
    d:=ord(key>t[k].key);                              //往哪走
    inset(t[k].ch[d],key);
    if t[t[k].ch[d]].fix>t[k].fix then rotate(k,d);    //维护堆的性质
end;

5、删除操作

找到删除结点的位置后有三种情况：

1、该节点有多个，也就是t[x].cnt>1：此时只要将t[x].cnt-1即可。

2、它只有一个儿子：用它的儿子来代替它。（没儿子直接删）

3、它有两个儿子：将它第二关键字值较大（若是小根堆则为较小）的节点旋上来，继续递归，直至到达1或2。

procedure delet(var k:longint;key:longint);
begin
    if k=0 then exit;                                          //找不到
    if t[k].key=key then
    begin
        if t[k].cnt>1 then                                     //情况1
            begin dec(t[k].cnt); dec(t[k].siz); exit; end;
        if (t[k].ch[0]=0)or(t[k].ch[1]=0) then                 //情况2
            begin k:=t[k].ch[0]+t[k].ch[1]; exit; end;
        rotate(k,ord(t[t[k].ch[0]].fix<t[t[k].ch[1]].fix));    //情况3
        delet(k,key);
    end else
    begin
        dec(t[k].siz);                                         //路径上的节点siz都减1
        delet(t[k].ch[ord(t[k].key<key)],key);                 //往哪走
    end;
end;

6、查排名

function rank(k,key:longint):longint;
begin
    if k=0 then exit(0);                                              //找不到
    if key=t[k].key then exit(t[t[k].ch[0]].siz)                      //找到了，这时整棵左子树都比它小
    else if key<t[k].key then exit(rank(t[k].ch[0],key))              //往左走
         else exit(t[t[k].ch[0]].siz+rank(t[k].ch[1],key)+t[k].cnt);  //往右走，这时整棵左子树和节点都比它小
end;

7、查找第k小数

感觉和上面查排名的操作差不多，就是反了一下罢了。（这里的k是节点编号，其实找的是第x小数）

和权值线段树上二分很像哦。

function find_kth(k,x:longint):longint;
begin
    if k=0 then exit(-1);                                           //找不到
    if x<=t[t[k].ch[0]].siz then exit(find_kth(t[k].ch[0],x));      //左子树规模比x大，说明在左子树中
    if x<=t[t[k].ch[0]].siz+t[k].cnt then exit(t[k].key);           //找到了
    exit(find_kth(t[k].ch[1],x-t[k].cnt-t[t[k].ch[0]].siz));        //在右子树中
end;

8、找前驱/后继

前驱就是在它的左子树中找一个最大的数，而后继则为在它的右子树中找一个最小的数。

在注意一下在找最大/最小值时别忘了它的父亲就行。（因为可能和它的值一样）

function find_pre(k,key:longint):longint;
begin
    if k=0 then exit(-maxlongint);
    if t[k].key>=key then exit(find_pre(t[k].ch[0],key));
    exit(max(find_pre(t[k].ch[1],key),t[k].key));
end;
function find_suc(k,key:longint):longint;
begin
    if k=0 then exit(maxlongint);
    if t[k].key<=key then exit(find_suc(t[k].ch[1],key));
    exit(min(find_suc(t[k].ch[0],key),t[k].key));
end;

下面附上我完整的代码：

type
    treap=record
        key,fix,cnt,siz:longint;
        ch:array[0..1]of longint;
    end;
var
    t:array[-1..100000]of treap;
    i,opt,x,cnt,q,root:longint;
function min(a,b:longint):longint;
begin
    if a<b then exit(a) else exit(b);
end;
function max(a,b:longint):longint;
begin
    if a>b then exit(a) else exit(b);
end;
procedure update(x:longint);
begin
    t[x].siz:=t[x].cnt+t[t[x].ch[0]].siz+t[t[x].ch[1]].siz;
end;
procedure rotate(var x:longint;d:longint);
var
    son:longint;
begin
    son:=t[x].ch[d];
    t[x].ch[d]:=t[son].ch[1-d];
    t[son].ch[1-d]:=x;
    update(x); update(son);
    x:=son;
end;
procedure inset(var k:longint;key:longint);
var
    d:longint;
begin
    if k=0 then
    begin
        inc(cnt); k:=cnt;
        t[k].key:=key; t[k].fix:=random(100000000);
        t[k].cnt:=1; t[k].siz:=1;
        exit;
    end else inc(t[k].siz);
    if t[k].key=key then begin inc(t[k].cnt); exit; end;
    d:=ord(key>t[k].key);
    inset(t[k].ch[d],key);
    if t[t[k].ch[d]].fix>t[k].fix then rotate(k,d);
end;
procedure delet(var k:longint;key:longint);
begin
    if k=0 then exit;
    if t[k].key=key then
    begin
        if t[k].cnt>1 then
            begin dec(t[k].cnt); dec(t[k].siz); exit; end;
        if (t[k].ch[0]=0)or(t[k].ch[1]=0) then
            begin k:=t[k].ch[0]+t[k].ch[1]; exit; end;
        rotate(k,ord(t[t[k].ch[0]].fix<t[t[k].ch[1]].fix));
        delet(k,key);
    end else
    begin
        dec(t[k].siz);
        delet(t[k].ch[ord(t[k].key<key)],key);
    end;
end;
function rank(k,key:longint):longint;
begin
    if k=0 then exit(0);
    if key=t[k].key then exit(t[t[k].ch[0]].siz)
    else if key<t[k].key then exit(rank(t[k].ch[0],key))
         else exit(t[t[k].ch[0]].siz+rank(t[k].ch[1],key)+t[k].cnt);
end;
function find_kth(k,x:longint):longint;
begin
    if k=0 then exit(-1);
    if x<=t[t[k].ch[0]].siz then exit(find_kth(t[k].ch[0],x));
    if x<=t[t[k].ch[0]].siz+t[k].cnt then exit(t[k].key);
    exit(find_kth(t[k].ch[1],x-t[k].cnt-t[t[k].ch[0]].siz));
end;
function find_pre(k,key:longint):longint;
begin
    if k=0 then exit(-maxlongint);
    if t[k].key>=key then exit(find_pre(t[k].ch[0],key));
    exit(max(find_pre(t[k].ch[1],key),t[k].key));
end;
function find_suc(k,key:longint):longint;
begin
    if k=0 then exit(maxlongint);
    if t[k].key<=key then exit(find_suc(t[k].ch[1],key));
    exit(min(find_suc(t[k].ch[0],key),t[k].key));
end;
begin
    randomize;
    read(q);
    root:=0;
    while q>0 do
    begin
        read(opt,x);
        if opt=1 then inset(root,x) else
        if opt=2 then delet(root,x) else
        if opt=3 then writeln(rank(root,x)+1) else
        if opt=4 then writeln(find_kth(root,x)) else
        if opt=5 then writeln(find_pre(root,x)) else
        if opt=6 then writeln(find_suc(root,x));
        dec(q);
    end;
end.