CTSC2010
星际旅行
https://www.luogu.com.cn/problem/P4189
题目:且每个星球的\(H_i\)大于等于与该星球直接相连的星球数(即度数)。
想到先从根到所有点都走一遍,然后贪心地考虑u到v的转移。
#include <bits/stdc++.h>
using namespace std;
namespace MAIN {
int n, h[50005], ans, ret[50005], son[50005];
vector<int> G[50005];
inline int read() {
int x = 0; char c = getchar();
while (c < '0' || c > '9') c = getchar();
while (c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
return x;
}
void dfs(int u, int fa) {
for (int i = 0; i < G[u].size(); ++i) {
int v = G[u][i];
if (v == fa) continue;
dfs(v, u);
int x = min(h[u], h[v]);
h[u] -= x, h[v] -= x;
ans += x * 2;
if (h[v]) son[u] = v;
}
}
void get(int u, int fa) {
ret[u] = ans;
for (int i = 0; i < G[u].size(); ++i) {
int v = G[u][i], t;
if (v == fa) continue;
if (h[u]) --h[u], ++ans, t = 1;
else if (son[v]) --h[son[v]], ++ans, t = 2;
else ++h[v], --ans, t = 3;
get(v, u);
if (t == 1) ++h[u], --ans;
else if (t == 2) ++h[son[v]], --ans;
else --h[v], ++ans;
}
}
inline int main() {
n = read();
for (int i = 1; i <= n; ++i) h[i] = read();
for (int i = 1; i < n; ++i) {
int u = read() + 1, v = read() + 1;
G[u].push_back(v);
G[v].push_back(u);
--h[u], --h[v];
ans += 2;
}
dfs(1, 0);
get(1, 0);
for (int i = 1; i <= n; ++i) printf("%d\n", ret[i]);
return 0;
}
} int main() { return MAIN::main(); }
产品销售
https://www.luogu.com.cn/problem/P4217
满足需求,并且耗费最少,考虑用模拟费用流。研究图的结构,发现是类似于
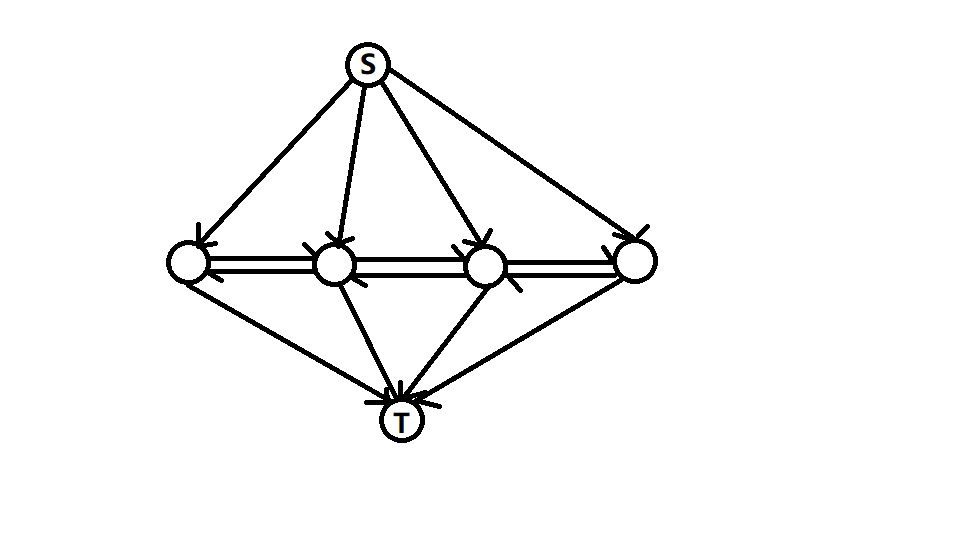
因为费用流中一定要流的边的增广的先后不影响答案,且和S、T连的边不会退流,考虑从左到右增广。
1.从左到右的边不会变,用直接维护最小值和位置就好了。
2.从右到左的边会出现反边(由之前的点从左到右增广产生)。显然最短路会先走负权边,所以只需一个线段树支持区间修改,最小值查询即可。当转移的点在边i左边时i的流量只会增加,在i右边时只会减小,所以一条边正负转化的次数是\(O(1)\)的,再建一颗线段树维护是否有边正负变化即可。
#include <bits/stdc++.h>
using namespace std;
namespace MAIN {
int n, D[100005], U[100005], P[100005], M[100005], C[100005], sc[100005], sm[100005];
long long ans;
inline int read() {
int x = 0; char c = getchar();
while (c < '0' || c > '9') c = getchar();
while (c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
return x;
}
namespace tree1 {
pair<int, int> t[400005];
void build(int p, int l, int r) {
if (l == r) { t[p] = make_pair(sc[l] + P[l], l); return; }
int mid = l + r >> 1;
build(p << 1, l, mid);
build(p << 1 | 1, mid + 1, r);
t[p] = min(t[p << 1], t[p << 1 | 1]);
}
pair<int, int> query(int p, int l, int r, int L, int R) {
if (l > R || L > r || L > R) return make_pair(2e9, -1);
if (L <= l && r <= R) return t[p];
int mid = l + r >> 1;
return min(query(p << 1, l, mid, L, R), query(p << 1 | 1, mid + 1, r, L, R));
}
void modify(int p, int l, int r, int x) {
if (l == r) { t[p] = make_pair(2e9, l); return; }
int mid = l + r >> 1;
if (x <= mid) modify(p << 1, l, mid, x);
else modify(p << 1 | 1, mid + 1, r, x);
t[p] = min(t[p << 1], t[p << 1 | 1]);
}
}
namespace tree3 {
pair<int, int> t[400005];
int tag[400005];
void push(int p) {
if (tag[p]) {
t[p << 1].first += tag[p];
t[p << 1 | 1].first += tag[p];
tag[p << 1] += tag[p];
tag[p << 1 | 1] += tag[p];
tag[p] = 0;
}
}
void build(int p, int l, int r) {
if (l == r) { t[p] = make_pair(sm[l] + P[l], l); return; }
int mid = l + r >> 1;
build(p << 1, l, mid);
build(p << 1 | 1, mid + 1, r);
t[p] = min(t[p << 1], t[p << 1 | 1]);
}
void add(int p, int l, int r, int L, int R, int x) {
if (l > R || L > r || L > R) return;
if (L <= l && r <= R) {
t[p].first += x;
tag[p] += x;
return;
}
push(p);
int mid = l + r >> 1;
add(p << 1, l, mid, L, R, x);
add(p << 1 | 1, mid + 1, r, L, R, x);
t[p] = min(t[p << 1], t[p << 1 | 1]);
}
pair<int, int> query(int p, int l, int r, int L, int R) {
if (l > R || L > r || L > R) return make_pair(2e9, -1);
if (L <= l && r <= R) return t[p];
push(p);
int mid = l + r >> 1;
return min(query(p << 1, l, mid, L, R), query(p << 1 | 1, mid + 1, r, L, R));
}
void modify(int p, int l, int r, int x) {
if (l == r) { t[p] = make_pair(2e9, l); return; }
int mid = l + r >> 1;
push(p);
if (x <= mid) modify(p << 1, l, mid, x);
else modify(p << 1 | 1, mid + 1, r, x);
t[p] = min(t[p << 1], t[p << 1 | 1]);
}
}
namespace tree2 {
int tag[400005], Min[400005], Max[400005];
inline void push(int p) {
if (tag[p]) {
tag[p << 1] += tag[p];
tag[p << 1 | 1] += tag[p];
Min[p << 1] += tag[p];
Min[p << 1 | 1] += tag[p];
Max[p << 1] += tag[p];
Max[p << 1 | 1] += tag[p];
tag[p] = 0;
}
}
int query(int p, int l, int r, int L, int R) {
if (l > R || L > r || L > R) return 2e9;
if (L <= l && r <= R) return Min[p];
int mid = l + r >> 1;
push(p);
return min(query(p << 1, l, mid, L, R), query(p << 1 | 1, mid + 1, r, L, R));
}
void add(int p, int l, int r, int L, int R, int x) {
if (l > R || L > r || L > R) return;
if (L <= l && r <= R) {
tag[p] += x;
Min[p] += x;
Max[p] += x;
return;
}
int mid = l + r >> 1;
push(p);
add(p << 1, l, mid, L, R, x);
add(p << 1 | 1, mid + 1, r, L, R, x);
Min[p] = min(Min[p << 1], Min[p << 1 | 1]);
Max[p] = max(Max[p << 1], Max[p << 1 | 1]);
}
void change0(int p, int l, int r, int L, int R) {
if (l > R || L > r || Max[p] < 2e9 || L > R) return;
if (l == r) {
tree3::add(1, 1, n, 1, l, -M[l] - C[l + 1]);
Min[p] = Max[p] = 0;
return;
}
int mid = l + r >> 1;
push(p);
change0(p << 1, l, mid, L, R);
change0(p << 1 | 1, mid + 1, r, L, R);
Min[p] = min(Min[p << 1], Min[p << 1 | 1]);
Max[p] = max(Max[p << 1], Max[p << 1 | 1]);
}
void change1(int p, int l, int r, int L, int R) {
if (l > R || L > r || Min[p] || L > R) return;
if (l == r) {
tree3::add(1, 1, n, 1, l, C[l + 1] + M[l]);
Min[p] = Max[p] = 2e9;
return;
}
int mid = l + r >> 1;
push(p);
change1(p << 1, l, mid, L, R);
change1(p << 1 | 1, mid + 1, r, L, R);
Min[p] = min(Min[p << 1], Min[p << 1 | 1]);
Max[p] = max(Max[p << 1], Max[p << 1 | 1]);
}
void build() { for (int i = 0; i <= 400000; ++i) Min[i] = Max[i] = 2e9; }
}
int main() {
#ifndef ONLINE_JUDGE
freopen("data.in", "r", stdin);
freopen("mine.out", "w", stdout);
#endif
n = read();
for (int i = 1; i <= n; ++i) D[i] = read();
for (int i = 1; i <= n; ++i) U[i] = read();
for (int i = 1; i <= n; ++i) P[i] = read();
for (int i = 1; i < n; ++i) M[i] = read();
for (int i = 2; i <= n; ++i) {
C[i] = read();
sc[i] = sc[i - 1] + C[i];
}
tree1::build(1, 1, n);
for (int i = n - 1; i >= 1; --i)
sm[i] = sm[i + 1] + M[i];
tree3::build(1, 1, n);
tree2::build();
for (int i = 1; i <= n; ++i) {
while (D[i]) {
pair<int, int> x = tree1::query(1, 1, n, i, n), y = tree3::query(1, 1, n, 1, i - 1);
x.first -= sc[i], y.first -= tree3::query(1, 1, n, i, i).first - P[i];
if (x < y) {
int flow = min(D[i], U[x.second]);
ans += 1ll * flow * x.first;
D[i] -= flow, U[x.second] -= flow;
if (U[x.second] == 0)
tree1::modify(1, 1, n, x.second);
tree2::change0(1, 1, n, i, x.second - 1);
tree2::add(1, 1, n, i, x.second - 1, flow);
} else {
int flow = min(min(D[i], U[y.second]), tree2::query(1, 1, n, y.second, i - 1));
ans += 1ll * flow * y.first;
D[i] -= flow, U[y.second] -= flow;
if (U[y.second] == 0)
tree3::modify(1, 1, n, y.second);
tree2::add(1, 1, n, y.second, i - 1, -flow);
tree2::change1(1, 1, n, y.second, i - 1);
}
}
}
printf("%lld\n", ans);
return 0;
}
} int main() { MAIN::main(); return 0; }
性能优化
https://www.luogu.com.cn/problem/P4191
观察代码发现求\(A*B^C\)的循环卷积。由单位根反演得只需求A、B、C的长度为n的dft序列即可。
由已知\((n + 1)\)的约数很小,fft把n分成d份即可。
#include <bits/stdc++.h>
using namespace std;
namespace MAIN {
int mod, n, C, g, a[500005], b[500005], aa[500005], c[10][500005];
vector<int> fac;
inline int read() {
int x = 0; char c = getchar();
while (c < '0' || c > '9') c = getchar();
while (c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
return x;
}
inline int fpow(int a, int b) {
int ret = 1;
for (; b; b >>= 1, a = 1ll * a * a % mod)
if (b & 1)
ret = 1ll * ret * a % mod;
return ret;
}
inline int getgen() {
vector<int> v;
for (int i = 2; i < mod - 1; ++i)
if ((mod - 1) % i == 0)
v.push_back(i);
for (int i = 2; ; ++i) {
bool flag = true;
for (const int &x : v)
if (fpow(i, x) == 1) {
flag = false;
break;
}
if (flag) return i;
}
}
inline void getfac() {
for (int i = 2, x = n; i <= 10; ++i) {
while (x % i == 0) {
fac.push_back(i);
x /= i;
}
}
}
void fft(int n, int *a, int t, int dep) {
if (n == 1) return;
int r = t == 1 ? fpow(g, (mod - 1) / n) : fpow(fpow(g, (mod - 1) / n), mod - 2);
int c[10][n / fac[dep]];
for (int i = 0; i < fac[dep]; ++i) {
for (int j = 0; j < n / fac[dep]; ++j)
c[i][j] = a[j * fac[dep] + i];
fft(n / fac[dep], c[i], t, dep + 1);
}
for (int i = 0, wi = 1; i < n; ++i, wi = 1ll * wi * r % mod) {
a[i] = 0;
for (int j = 0, w = 1; j < fac[dep]; ++j, w = 1ll * w * wi % mod)
a[i] = (a[i] + 1ll * w * c[j][i % (n / fac[dep])]) % mod;
}
}
int main() {
n = read(), C = read(), mod = n + 1, g = getgen(), getfac();
for (int i = 0; i < n; ++i) a[i] = read();
for (int i = 0; i < n; ++i) b[i] = read();
fft(n, a, 1, 0);
fft(n, b, 1, 0);
for (int i = 0; i < n; ++i) a[i] = 1ll * a[i] * fpow(b[i], C) % mod;
fft(n, a, -1, 0);
for (int i = 0, inv = fpow(n, mod - 2); i < n; ++i) printf("%d\n", 1ll * a[i] * inv % mod);
return 0;
}
} int main() { MAIN::main(); return 0; }
珠宝商
https://www.luogu.com.cn/problem/P4218
看到求所有路径的和,容易想到点分治、后缀自动机。发现对于每个\(u\)对答案的贡献为
\(\sum\limits_{p=1}^m\sum\limits_{a}\sum\limits_{b}[a到u在模式串的结束位置为p]且[u到b在模式串的开始位置为p]\)
发现右边的式子和左边的式子是同理的,只需把字符串翻转一下即可。
考虑\(\sum\limits_{a}[a到u在模式串的结束位置为p]\)
设在当前自动机上的节点为x,只需处理出在当前节点的前面加字符c的转移即可(一般是往后加)
1. 长度<val[x], 只需判断前一个是否是c即可
2. 长度=val[x], 通过x在parent树上的儿子来转移(儿子的val比父亲大)
复杂度是假的,菊花图就爆了。感觉可以再用数据结构维护一下,不写了:)
#include <bits/stdc++.h>
using namespace std;
namespace MAIN {
vector<int> G[50005];
bool flag[50005];
int n, m, S, root, mxs[50005], pos1[50005], pos2[50005], W;
char a[50005], s[50005];
long long ans;
struct SAM {
int val[100005], par[100005], go[100005][26], root, ncnt, last, R[100005], s[50005], siz[100005], fr[100005][26], js[50005], id[100005], num[100005];
SAM() { root = ncnt = last = 1; }
inline void extend(int w) {
int p = last, np = ++ncnt;
val[np] = val[p] + 1;
R[np] = val[np];
siz[np] = 1;
for (; p && go[p][w] == 0; p = par[p]) go[p][w] = np;
if (p == 0) par[np] = root;
else {
int q = go[p][w];
if (val[q] == val[p] + 1) par[np] = q;
else {
int nq = ++ncnt;
val[nq] = val[p] + 1;
memcpy(go[nq], go[q], sizeof(go[q]));
par[nq] = par[q];
par[q] = nq;
par[np] = nq;
for (; p && go[p][w] == q; p = par[p]) go[p][w] = nq;
}
}
last = np;
}
inline void pre() {
for (int i = 1; i <= ncnt; ++i) ++js[val[i]];
for (int i = 1; i <= m; ++i) js[i] += js[i - 1];
for (int i = 1; i <= ncnt; ++i) id[js[val[i]]--] = i;
for (int i = ncnt; i >= 1; --i) {
int u = id[i];
siz[par[u]] += siz[u];
R[par[u]] = R[u];
fr[par[u]][s[R[u] - val[par[u]]]] = u;
}
}
inline void calc(int u, int fa, int p, int len) {
if (len == val[p]) p = fr[p][a[u]];
else if (s[R[p] - len] != a[u]) p = 0;
if (p == 0) return;
++num[p], ++len;
for (auto &v : G[u])
if (!flag[v] && v != fa)
calc(v, u, p, len);
}
inline void pushdown() {
for (int i = 1; i <= ncnt; ++i)
num[id[i]] += num[par[id[i]]];
}
} s1, s2;
inline int read() {
int x = 0; char c = getchar();
while (c < '0' || c > '9') c = getchar();
while (c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
return x;
}
inline void getrt(int u) {
function<int(int, int)> count = [&](int u, int fa) {
int siz = 1;
for (auto &v : G[u]) {
if (flag[v] || v == fa) continue;
siz += count(v, u);
}
return siz;
};
S = count(u, 0), root = -1;
function<int(int, int)> find = [&](int u, int fa) {
int siz = 1;
for (auto &v : G[u]) {
if (flag[v] || v == fa) continue;
siz += find(v, u);
}
mxs[u] = max(siz, S - siz);
if (root == -1 || mxs[u] < mxs[root]) root = u;
return siz;
};
find(u, 0);
}
inline void calc(int u, int fa, int op) {
memset(s1.num, 0, sizeof(s1.num));
memset(s2.num, 0, sizeof(s2.num));
if (op == 1) {
s1.calc(u, 0, 1, 0);
s2.calc(u, 0, 1, 0);
} else {
s1.calc(u, fa, s1.go[1][a[fa]], 1);
s2.calc(u, fa, s2.go[1][a[fa]], 1);
}
s1.pushdown();
s2.pushdown();
for (int i = 1; i <= m; ++i)
ans += op * s1.num[pos1[i]] * s2.num[pos2[m + 1 - i]];
}
void div(int u) {
if (S <= W) {
function<void(int, int)> meiju = [&](int u, int fa) {
function<void(int, int, int)> work = [&](int u, int fa, int p) {
if (p == 0) return;
ans += s1.siz[p];
for (auto &v : G[u])
if (!flag[v] && v != fa)
work(v, u, s1.go[p][a[v]]);
};
work(u, 0, s1.go[1][a[u]]);
for (auto &v : G[u])
if (!flag[v] && v != fa)
meiju(v, u);
};
meiju(u, 0);
return;
}
flag[u] = 1;
calc(u, u, 1);
for (auto &v : G[u]) {
if (flag[v]) continue;
calc(v, u, -1);
getrt(v);
div(root);
}
}
inline int main() {
n = read(), m = read(), W = sqrt(n);
for (int i = 1; i < n; ++i) {
int u = read(), v = read();
G[u].push_back(v);
G[v].push_back(u);
}
scanf("%s", a + 1);
for (int i = 1; i <= n; ++i) a[i] -= 'a';
scanf("%s", s + 1);
for (int i = 1; i <= m; ++i) s[i] -= 'a';
for (int i = 1; i <= m; ++i) s1.extend(s[i]), pos1[i] = s1.last, s1.s[i] = s[i];
for (int i = 1; i <= m; ++i) s2.extend(s[m + 1 - i]), pos2[i] = s2.last, s2.s[i] = s[m + 1 - i];
s1.pre(), s2.pre();
getrt(1);
div(root);
printf("%lld\n", ans);
return 0;
}
} int main() { return MAIN::main(); }
三国围棋擂台赛
https://www.luogu.com.cn/problem/P4190
很明显的状压dp,注意先把每队的第一个人手算出来,再dp。
#include <bits/stdc++.h>
using namespace std;
namespace MAIN {
double dp[65][65][65][3][3][8], a_b[10][10], a_c[10][10], b_c[10][10], ans;
int n;
inline double min(const double &x, const double &y) { return x < y ? x : y; }
inline double max(const double &x, const double &y) { return x > y ? x : y; }
double fun(int sa, int sb, int sc, int x, int y, int l) {
if (sa == 0 && x != 0) return 0;
if (sb == 0 && sc == 0 && x == 0) return 1;
if (dp[sa][sb][sc][x][y][l] > -1) return dp[sa][sb][sc][x][y][l];
double ret;
if (x == 0) {
if (sc == 0 || (sb != 0 && y == 1)) {
ret = 1;
for (int i = 1; i < n; ++i)
if (sb >> i - 1 & 1)
ret = min(ret, a_b[l][i] * fun(sa, sb ^ 1 << i - 1, sc, 0, 2, l) + (1 - a_b[l][i]) * fun(sa, sb ^ 1 << i - 1, sc, 1, 2, i));
} else {
ret = 1;
for (int i= 1; i < n; ++i)
if (sc >> i - 1 & 1)
ret = min(ret, a_c[l][i] * fun(sa, sb, sc ^ 1 << i - 1, 0, 1, l) + (1 - a_c[l][i]) * fun(sa, sb, sc ^ 1 << i - 1, 2, 1, i));
}
} else if (x == 1) {
if (sc == 0 || (sa != 0 && y == 0)) {
ret = 0;
for (int i = 1; i < n; ++i)
if (sa >> i - 1 & 1)
ret = max(ret, a_b[i][l] * fun(sa ^ 1 << i - 1, sb, sc, 0, 2, i) + (1 - a_b[i][l]) * fun(sa ^ 1 << i - 1, sb, sc, 1, 2, l));
} else {
ret = 1;
for (int i = 1; i < n; ++i)
if (sc >> i - 1 & 1)
ret = min(ret, b_c[l][i] * fun(sa, sb, sc ^ 1 << i - 1, 1, 0, l) + (1 - b_c[l][i]) * fun(sa, sb, sc ^ 1 << i - 1, 2, 0, i));
}
} else {
if (sb == 0 || (sa != 0 && y == 0)) {
ret = 0;
for (int i = 1; i < n; ++i)
if (sa >> i - 1 & 1)
ret = max(ret, a_c[i][l] * fun(sa ^ 1 << i - 1, sb, sc, 0, 1, i) + (1 - a_c[i][l]) * fun(sa ^ 1 << i - 1, sb, sc, 2, 1, l));
} else {
ret = 1;
for (int i = 1; i < n; ++i)
if (sb >> i - 1 & 1)
ret = min(ret, b_c[i][l] * fun(sa, sb ^ 1 << i - 1, sc, 1, 0, i) + (1 - b_c[i][l]) * fun(sa, sb ^ 1 << i - 1, sc, 2, 0, l));
}
}
return dp[sa][sb][sc][x][y][l] = ret;
}
inline int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
scanf("%lf", &a_b[i][j]);
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
scanf("%lf", &a_c[i][j]);
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
scanf("%lf", &b_c[i][j]);
int st = (1 << n - 1) - 1;
for (int i = 0; i <= st; ++i)
for (int j = 0; j <= st; ++j)
for (int k = 0; k <= st; ++k)
for (int x = 0; x < 3; ++x)
for (int y = 0; y < 3; ++y)
for (int l = 1; l <= n; ++l)
dp[i][j][k][x][y][l] = -1;
ans += 1.0 / 3 * (a_b[n][n] * (a_c[n][n] * fun(st, st, st, 0, 1, n) + (1 - a_c[n][n]) * fun(st, st, st, 2, 1, n)) +
(1 - a_b[n][n]) * (b_c[n][n] * fun(st, st, st, 1, 0, n) + (1 - b_c[n][n]) * fun(st, st, st, 2, 0, n)));
ans += 1.0 / 3 * (a_c[n][n] * (a_b[n][n] * fun(st, st, st, 0, 2, n) + (1 - a_b[n][n]) * fun(st, st, st, 1, 2, n)) +
(1 - a_c[n][n]) * (b_c[n][n] * fun(st, st, st, 1, 0, n) + (1 - b_c[n][n]) * fun(st, st, st, 2, 0, n)));
ans += 1.0 / 3 * (b_c[n][n] * (a_b[n][n] * fun(st, st, st, 0, 2, n) + (1 - a_b[n][n]) * fun(st, st, st, 1, 2, n)) +
(1 - b_c[n][n]) * (a_c[n][n] * fun(st, st, st, 0, 1, n) + (1 - a_c[n][n]) * fun(st, st, st, 2, 1, n)));
printf("%.6lf\n", ans);
return 0;
}
} int main() { return MAIN::main(); return 0; }
CTSC2010的更多相关文章
- [CTSC2010]珠宝商 SAM+后缀树+点分治
[CTSC2010]珠宝商 不错的题目 看似无法做,n<=5e4,8s,根号算法? 暴力一: n^2,+SAM上找匹配点的right集合sz,失配了直接退出 暴力二: O(m) 统计过lca=x ...
- [CTSC2010]性能优化
[CTSC2010]性能优化 循环卷积快速幂 两个注意点:n+1不是2^k*P+1形式,任意模数又太慢?n=2^k1*3^k2*5^k3*7^k4 多路分治!深刻理解FFT运算本质:分治,推式子得到从 ...
- 【BZOJ1921】【CTSC2010】珠宝商(点分治,后缀自动机)
[BZOJ1921][CTSC2010]珠宝商(点分治,后缀自动机) 题面 洛谷 BZOJ权限题 题解 如果要我们做暴力,显然可以以某个点为根节点,然后把子树\(dfs\)一遍,建出特征串的\(SAM ...
- P4218 [CTSC2010]珠宝商
P4218 [CTSC2010]珠宝商 神题... 可以想到点分治,细节不写了... (学了个新姿势,sam可以在前面加字符 但是一次点分治只能做到\(O(m)\),考虑\(\sqrt n\)点分治, ...
- 「CTSC2010」产品销售
「CTSC2010」产品销售 30pts的费用流都会吧... 100pts只要模拟费用流就行了,是不是很简单呀( 咕咕咕 令\(M_i\)表示\(i-1\to i\)的正向边,\(M_i^{'}\)表 ...
- Luogu4191:[CTSC2010]性能优化
传送门 题目翻译:给定两个 \(n\) 次多项式 \(A,B\) 和一个整数 \(C\),求 \(A\times B^C\) 在模 \(x^n\) 意义下的卷积 显然就是个循环卷积,所以只要代入 \( ...
- [CTSC2010]星际旅行
https://www.luogu.org/problemnew/show/P4189 题解 模拟费用流. 首先有一个非常好的条件,每个点的限制次数都大于等于这个点的度数. 然后我们可以从\(0\)开 ...
- [BZOJ1921] [CTSC2010]珠宝商
Description Input 第一行包含两个整数 N,M,表示城市个数及特征项链的长度. 接下来的N-1 行, 每行两个整数 x,y, 表示城市 x 与城市 y 有直接道路相连.城市由1~N进行 ...
- Bzoj1917 [Ctsc2010]星际旅行
Time Limit: 10 Sec Memory Limit: 259 MBSubmit: 185 Solved: 118 Description 公元3000年,地球联盟已经攻占了银河系内的N ...
- 洛谷P4218 [CTSC2010]珠宝商(后缀自动机+点分治)
传送门 这题思路太清奇了……->题解 //minamoto #include<iostream> #include<cstdio> #include<cstring ...
随机推荐
- 嵌入式Linux软链接使用技巧
软链接概述 软链接是Linux下常用的一种共享文件方式.目录的方式,这种方式类似于Windows下的快捷方式.一般一个文件或者目录在不同的路径都需要的时候,可以通过创建软链接的方式来共享,这样只系统下 ...
- 浅谈Java 线程池原理及使用方式
一.简介 什么是线程池? 池的概念大家也许都有所听闻,池就是相当于一个容器,里面有许许多多的东西你可以即拿即用.java中有线程池.连接池等等.线程池就是在系统启动或者实例化池时创建一些空闲的线程,等 ...
- js垃圾回收和内存泄漏
js垃圾回收和内存泄漏 js垃圾回收 Js具有自动垃圾回收机制.垃圾收集器会按照固定的时间间隔周期性的执行. 1.标记清除(常用) 工作原理:是当变量进入环境时,将这个变量标记为"进入环境& ...
- VSM
好吧,在被这个算法折腾了许多天之后,我终于对它竖起了中指.这几天的经历让我明白了一个道理:对于数学基础不好的人来说,对待图形学最好远观不可亵玩焉:如果坚持硬闯却又碰巧E文不咋地,那受罪程度真叫人生不如 ...
- linux中root用户查看所有用户的历史操作命令
转载https://blog.csdn.net/qq_27786919/article/details/91353351 1.创建用户审计文件存放目录和审计日志文件 :mkdir -p /var/lo ...
- oracle之事务和锁
Oracle的事务和锁(PPT-I-283-293) 10.1 什么是事务 必须具备以下四个属性,简称ACID 属性:原子性(Atomicity): 事务是一个完整的操作.事务的各步操作是不可分的( ...
- 突发!美商务部宣布封禁微信,TikTok——面对科技封锁,如何应对
刚刚美国商务部忽然发布了这则新闻,为了回应特朗普2020年8月6号的行政令,称这些应用程序存在安全威胁. 禁令中称,自2020年9月20日起,美国政府将: 1 禁止通过美国在线移动应用程序商店分发或维 ...
- 【读书】Into The Air:进入空气稀薄地带
珠穆朗玛峰,世界第一高峰,北部在中国境内,南部在尼泊尔境内.喜欢户外运动的人,曾经在20多岁的时候曾经"大言不惭"说这一辈子一定要去一次珠峰.<Into the Air> ...
- Redis可视化工具推荐
前言 Redis可视化工具目前好用的免费的几乎难以寻迹,百度能搜索到的推荐比较多的是Redis Desktop Manager 官网地址:https://redisdesktop.com/pricin ...
- kali上密码工具使用例如mudusa,hydra等
思路 各种密码类别大致数学原理 https://blog.csdn.net/carol980206/article/details/96705859 https://www.jianshu.com/p ...
