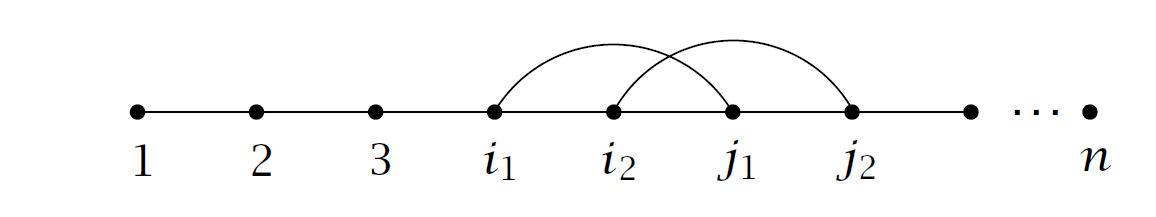The Involution Principle

Catalan Paths
Vandermonde Determinant
The Pfaffian

Catalan Paths

从 $(0,0)$ 走到 $(n,n)$, 每次只能向上或者向右走，不能穿过直线 $y=x$ 的方案数。

设从 $(0,0)$ 到 $(n,n)$ 的路径集合为 $S$，从 $(1,0)$ 到 $(n+1,n)$ 的路经集合 $S^+$，从 $(0,1)$ 到 $(n+1,n)$ 的路经集合 $S^-$，显然有 $|S^+|=\binom{2n}{n},|S^-|=\binom{2n}{n-1}$。对于一条路径 $W\in S^+\cup S^-$，让 $\phi W$ 表示一条路径，如果 $W$ 没有穿过 $y=x$，那么 $\phi W=W$，否则 $\phi W$ 表示 $W$ 关于 $W$ 与 $y=x$ 的第一个交点的对称路径。

显然对于任意一条路径 $W\in S^-$，它都会穿过 $y=x$，并且 $\phi W\in S^+$，所以 $C_n=\binom{2n}{n}-\binom{2n}{n-1}=\frac{\binom{2n}n}{n+1}$

Vandermonde Determinant

$\det\begin{gathered}\begin{pmatrix} x_1^{n-1} & x_2^{n-1} & ... & x_n^{n-1} \\ x_1^{n-2} & x_2^{n-2} & ... & x_n^{n-2} \\ ... \\ x_1 & x_2 & ... & x_n \\ 1 & 1 & ... & 1 \end{pmatrix}\end{gathered}=\prod\limits_{1\le i<j\le n}(x_i-x_j)$

Proof.

$\text{The left-hand side}\colon\sum\limits_{\sigma\in S(n)}(\text{sign }\sigma)x_{\sigma(1)}^{n-1}x_{\sigma(2)}^{n-2}\cdots x_{\sigma(n)}^0$

$\text{The right-hand side}\colon(-1)^mx_1^{a_1}x_2^{a_2}\cdots x_n^{a_n}\ (\sum\limits_{i=1}^na_i=\binom{n}{2},m=\#\{j\colon x_j\text{ is taken from }x_i-x_j\})$

考虑建立竞赛图 $T$，对于一条边 $e=(u,v)$ 我们称 $u$ 是赢家，并定义 $e$ 的权重:$w(e)=x_u\text{ with sign }e=\begin{cases}1 & u<v\\-1 & u>v\end{cases}$

再定义 $w(T)=\prod\limits_{e\in T}w(e),\text{sign }T=\prod\limits_{e\in T}\text{ sign }e$

那显然就有 $\prod\limits_{1\le i<j\le n}=\sum\limits_{T}(\text{sign }T)w(T)$

从另一个方面也很好解释为啥这两个很容易能看成相等的，因为竞赛图个数和 $\prod\limits_{1\le i<j\le n}$ 拆开之后的项数都是 $2^{\binom{n}{2}}$

于是现在只需要建立竞赛图与行列式的关系。

首先考虑所有无环的竞赛图，显然可以给 $1,2...n$ 排一个序构成排列 $\sigma$，容易观察到 $w(T_{\sigma})=x_{\sigma(1)}^{n-1}x_{\sigma(2)}^{n-2}\cdots x_{\sigma(n)^0},\text{ sign }T_{\sigma}=(-1)^{\text{inv }\sigma}=\text{sign }\sigma$

所以有 $\det=\sum\limits_{\sigma\in S(n)}(\text{sign }\sigma)w(T_{\sigma})$

现在考虑想办法过滤掉有环的竞赛图，让集合 $S$ 表示所有有环的竞赛图集合， $S^+=\{T\in S\colon \text{sign }T=1\},S^-=\{T\in S\colon \text{sign }T=-1\}$

对于一个有环的竞赛图 $T$，显然会存在一些点对使得其入度相同，我们找出所有点对中最小的点 $i_0$ 和与 $i_0$ 入度相同的最小的点 $j_0$，那么对于一个点 $k\not= i_0, j_0$，不妨设 $i_0\rightarrow j_0$，那么三元组 $i_0,j_0,k$ 之间的连边关系只可能有下面四种情况:

显然有 $\#\text{II}=\#\text I + 1$

考虑设 $\phi T$ 表示图 $T$ 将边 $(i_0,j_0)$ 反向后得到的新图，显然有 $\text{sign }T=-\text{sign }\phi T,w(T)=w(\phi T)$，且一个在 $S^+$ 中，一个在 $S^{-}$ 中，于是这些图的贡献会被抵消掉，故原式得证.

The Pfaffian

称对于集合 $\{1,2...n\}$ 的任意一个两两划分为在 $\{1,2...n\}$上的一个匹配 $\mu$，写作 $\mu=i_1j_1,i_2j_2,...,i_{n/2}j_{n/2}\text{ with }i_k<j_k\text{ for all }k$，对于一个斜对称矩阵 $A$，我们记一个符号 $a_{\mu}=a_{i_1j_1}a_{i_2j_2}\cdots a_{i_{n/2}j_{n/2}}$

为了定义 $\mu$ 的符号，考虑画图列出 $1,2...;\#\mu$ 表示匹配交叉的数量，并且 $\text{sign }\mu=(-1)^{\#\mu}$

对于这个矩阵 $A$，我们定义 $pfaffian\text{ Pf}(A)=\sum\limits_{\mu}(\text{sign }\mu)a_{\mu}$

那么有定理 $\det A=[\text{Pf}(A)]^2$

Proof.

首先还是考虑行列式的常见形式 $\det A=\sum\limits_{\sigma\in S(n)}(\text{sign }\sigma)a_{\sigma}\ (a_{\sigma}=a_{1\sigma(1)}a_{2\sigma(2)}\cdots a_{n\sigma(n)})$

定义 $S$ 是所有排列中至少包含一个奇环的排列的集合。对于 $\sigma\in S,\text{let }\sigma=\sigma_1\sigma_2\cdots\sigma_t$ 为其环分解，其中 $\sigma_1$ 是所有奇环中最小标号所在的奇环，然后定义

显然除了 $\sigma_1=(k)$ 的情况有 $a_{\sigma}=-a_{\sigma'},(\text{sign }\sigma)a_{\sigma}=-(\text{sign }\sigma')a_{\sigma'}$，而对于 $\sigma_1=(k)$ 的情况，显然有 $a_{\sigma}=0$。

于是可以获得结论:$\det A=\sum\limits_{\sigma\in E}(\text{sign }\sigma)a_{\sigma}$，其中 $E\in S(n)$ 是所有只包含偶环的排列。

要证明定理，需要找到一个 $(\mu_1,\mu_2)$ 到 $\sigma\in E$ 的双射关系 $\phi$ 使得 $(\text{sign }\mu_1)a_{\mu_1}\cdot (\text{sign }\mu_2)a_{\mu_2}=(\text{sign }\sigma)a_{\sigma}$，这里简单举一个例子:

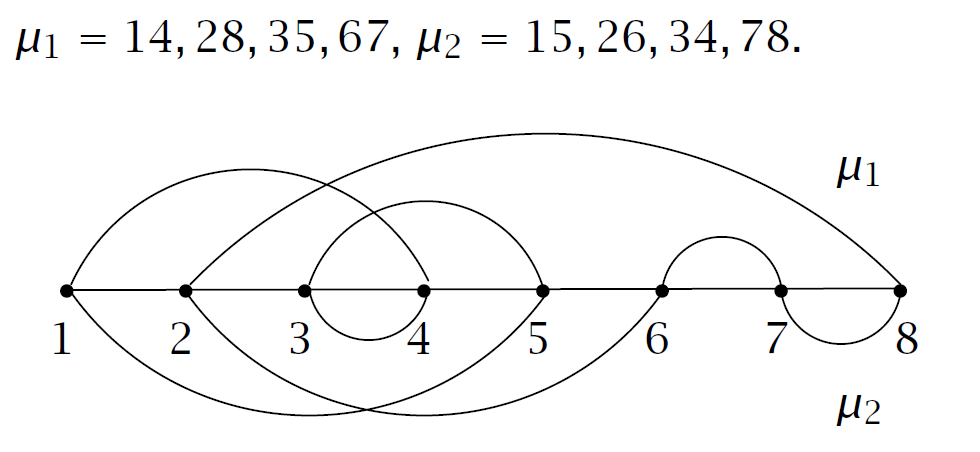
先不考虑符号的问题观察一番。

考虑正向拼凑 $\sigma$，考虑如下过程:每次选出未访问过的最小标号点，然后依次沿着 $\mu1,\mu2$ 中的匹配边走，最后一定会走出若干个偶环。

考虑反向求 $\mu1,\mu2$ ，考虑如下过程:每次选一个偶环，从上面的最小标号点开始依次把边划分给 $\mu1,\mu2$。

现在就只用考虑符号是否能对上。

假设 $\phi(\mu_1,\mu_2)=(-1)^{e(\sigma)}a_{\sigma},e_(\sigma)=\#\{i\colon i>\sigma(i)\}$

令 $\sigma$ 的环分解是 $\sigma_1\sigma_2\cdots\sigma_t;$ 那么 $\text{sign }\sigma=(-1)^t$

所以只需要证明 $\text{sign }\mu_1\cdot\text{sign }\mu_2=(-1)^{e(\sigma)+t}$ 即 $\#\mu_1+\#\mu_2-e(\sigma)\equiv t\ (\text{mod 2})$

容易证明，对于这个环分解，如果我们交换 $i,i+1$ 的位置，得到的 $\#\mu_1'+\#\mu_2'-e(\sigma)'$ 和 $\#\mu_1+\#\mu_2-e(\sigma)$ 奇偶性相同，故可以把 $\sigma$ 经过多次交换变成

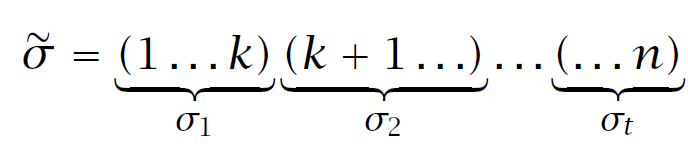
把匹配画出来显然长这样

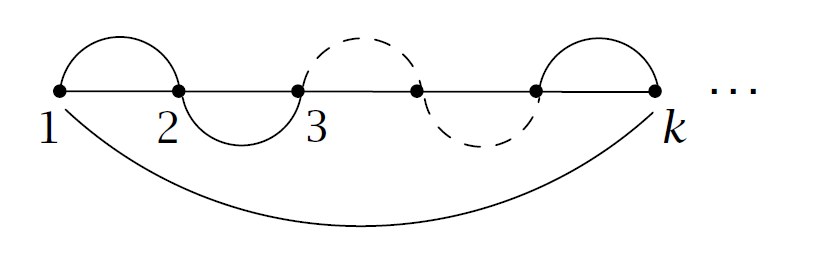
显然对于这个东西， $\#\mu_1'=\#\mu_2'=0,e(\sigma)'=t$ ，故原定理得证.