题解-洛谷P4724 【模板】三维凸包

洛谷P4724 【模板】三维凸包

给出空间中 \(n\) 个点 \(p_i\)，求凸包表面积。

数据范围：\(1\le n\le 2000\)。

---

这篇题解因为是世界上最逊的人写的，所以也会有求凸包体积的讲解。

---

三位向量的运算

• 模长： 即向量长度，\(|\vec{a}|=\sqrt{x_a^2+y_a^2+z_a^2}\)。

• 点积： 标量 \(\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos<\vec{a},\vec{b}>=x_ax_b+y_ay_b+z_az_b\)，为 \(\vec{a}\) 的模长乘以 \(\vec{b}\) 在 \(\vec{a}\) 上的投影的模长。

• 叉积： 向量 \(\vec{a}*\vec{b}=(y_az_b-z_ay_b,z_ax_b-x_az_b,x_ay_b-y_ax_b)\)，模长为平四面积。

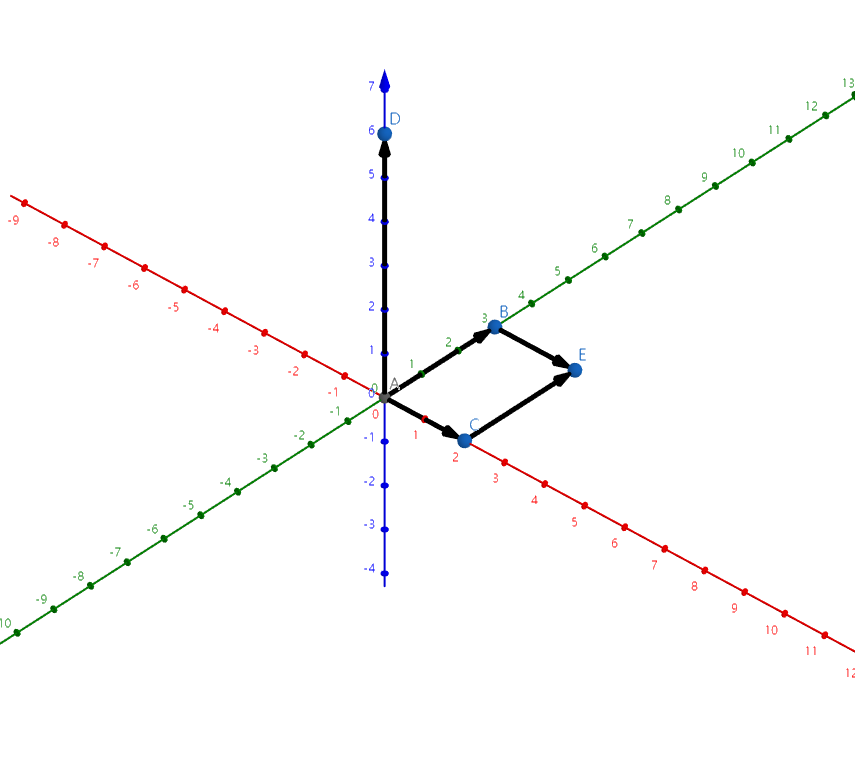
上图 \(\vec{AC}*\vec{AB}=\vec{AD}\)，\(\vec{AD}\) 垂直 \(\vec{AC}\) 与 \(\vec{AB}\) 的平面，模长为平四面积。

---

会用到的计算与判定

• 判断点 \(E\) 在平面 \(ABC\) 上方：

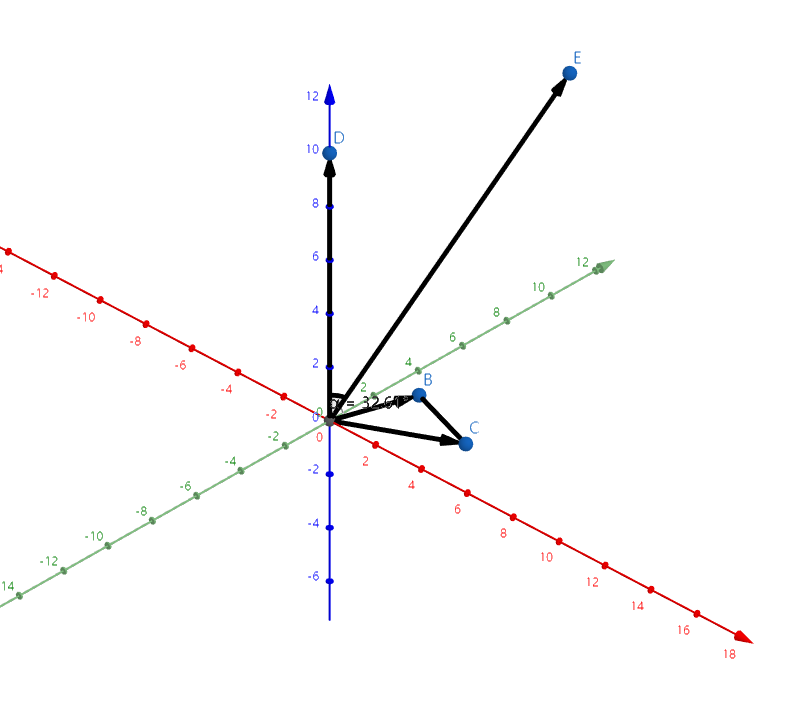
作 \(\vec{AD}=\vec{AC}*\vec{AB}\)，用 \(\vec{AE}\cdot \vec{AD}>0\) 来判断 \(\angle DAE<\frac{\pi}{2}\)。

• 求点 \(E\) 到平面 \(ABC\) 的距离：

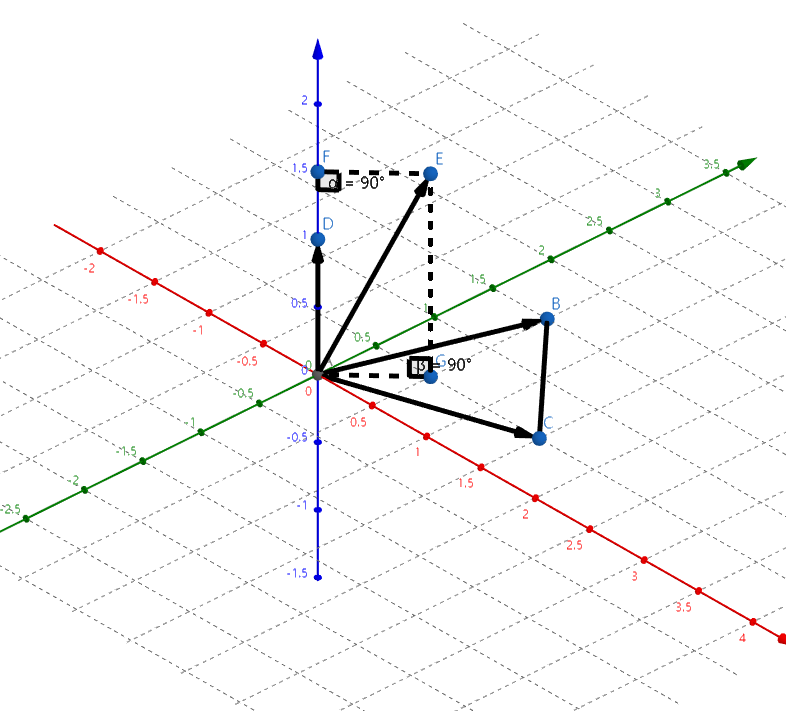
距离 \({\rm dist}(E,\triangle ABC)=EG=AF=\frac{\vec{AD}\cdot \vec{AE}}{|\vec{AD}|}=\frac{\vec{AD}\cdot \vec{AE}}{|\vec{AC}*\vec{AB}|}\)。

---

处理凸包

设凸包为 \(Con\)，用逆时针顺序三个点表示一个三角形面。

每加入一个新点 \(p_{new}\) 的时候，把它当作光源照向之前的凸包，将未照到的面留下，加上 \(p_{new}\) 和光影边缘形成的新面。

引用巨佬的图：

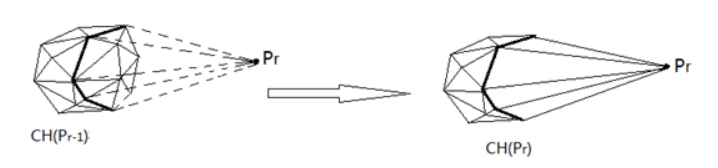
判断照不照得到用判定“点 \(E\) 在平面 \(ABC\) 上方”的方法。

判断光影边缘用 \(vis\) 数组。\(vis_{i,j}\) 表示 \((i,j,k)\)（即 \((i,j)\) 逆时针方向上的面）这个面是否照光，如果 \([vis_{i,j}=1]\&\&[vis_{j,i}=0]\)，说明 \((i,j)\) 是光影边缘，需加面 \((i,j,p_{new})\)。

重复加点，得到 \(m\) 个 \(Con\) 上的面 \(f_i=(A,C,B)\)。

\[\sum_{i=1}^m S_i=\sum\frac{|\vec{AC}*\vec{AB}|}{2}
\]

\[V_{Con}=\sum \frac{\frac{|\vec{AC}*\vec{AB}|}{2}\cdot {\rm dist}(D,f_i)}{3}
\]

其中 \(D\) 是一个定点，需要在 \(Con\) 内或表面上，可以选 \(p_1\)，上面是三棱锥体积计算公式。

---

时间复杂度 \(\Theta(n^2)\)，空间复杂度 \(\Theta(n^2)\)。

每加入一个点，面最多增加 \(2\) 个。

证明：设光影边缘上有 \(n\) 个点，因为每个面是三角形，所以要去掉的面 \(\ge n-2\)（中间可能有点），增加的面数为 \(n\)，所以增加的点数 \(\le 2\)。

---

代码

• 求表面积

#include <bits/stdc++.h>
using namespace std;

//Start
typedef long long ll;
typedef double db;
#define mp(a,b) make_pair(a,b)
#define x first
#define y second
#define be(a) a.begin()
#define en(a) a.end()
#define sz(a) int((a).size())
#define pb(a) push_back(a)
const int inf=0x3f3f3f3f;
const ll INF=0x3f3f3f3f3f3f3f3f;

//Data
const int N=2000;
const db eps=1e-9;
int n,m;
db ans;

//Convex
mt19937 orz(time(0));
db reps(){return (1.*(orz()%98)/97-.5)*eps;}
struct point{
	db x,y,z;
	void shake(){x+=reps(),y+=reps(),z+=reps();}
	db len(){return sqrt(x*x+y*y+z*z);}
	point operator-(point p){return (point){x-p.x,y-p.y,z-p.z};}
	point operator*(point p){return (point){y*p.z-p.y*z,z*p.x-p.z*x,x*p.y-p.x*y};}
	db operator^(point p){return x*p.x+y*p.y+z*p.z;}
}a[N];
struct plane{
	int v[3];
	point flag(){return (a[v[1]]-a[v[0]])*(a[v[2]]-a[v[0]]);}
	db area(){return flag().len()/2;}
	int see(point p){return ((p-a[v[0]])^flag())>0;}
}f[N],g[N];
int vis[N][N];
void Convex(){
	#define ft f[j].v[t]
	#define bk f[j].v[(t+1)%3]
	f[m++]=(plane){0,1,2},f[m++]=(plane){2,1,0};
	for(int i=3;i<n;i++){
		int cnt=0,b;
		for(int j=0;j<m;j++){
			if(!(b=f[j].see(a[i]))) g[cnt++]=f[j];
			for(int t=0;t<3;t++) vis[ft][bk]=b;
		}
		for(int j=0;j<m;j++)
			for(int t=0;t<3;t++)
				if(vis[ft][bk]&&!vis[bk][ft]) g[cnt++]=(plane){ft,bk,i};
		m=cnt;
		for(int j=0;j<m;j++) f[j]=g[j];
	}
} 

//Main
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=0;i<n;i++) cin>>a[i].x>>a[i].y>>a[i].z,a[i].shake();
	Convex();
	for(int i=0;i<m;i++) ans+=f[i].area();
	cout.precision(3);
	cout<<fixed<<ans<<'\n';
	return 0;
}

• 求体积

#include <bits/stdc++.h>
using namespace std;

//Start
typedef long long ll;
typedef double db;
#define mp(a,b) make_pair(a,b)
#define x first
#define y second
#define be(a) a.begin()
#define en(a) a.end()
#define sz(a) int((a).size())
#define pb(a) push_back(a)
const int inf=0x3f3f3f3f;
const ll INF=0x3f3f3f3f3f3f3f3f;

//Data
const int N=2000;
const db eps=1e-9;
int n,m;
db ans;

//Convex
mt19937 orz(time(0));
db reps(){return (1.*(orz()%98)/97-.5)*eps;}
struct point{
	db x,y,z;
	void shake(){x+=reps(),y+=reps(),z+=reps();}
	db len(){return sqrt(x*x+y*y+z*z);}
	point operator-(point p){return (point){x-p.x,y-p.y,z-p.z};}
	point operator*(point p){return (point){y*p.z-p.y*z,z*p.x-p.z*x,x*p.y-p.x*y};}
	db operator^(point p){return x*p.x+y*p.y+z*p.z;}
}a[N];
struct plane{
	int v[3];
	point flag(){return (a[v[1]]-a[v[0]])*(a[v[2]]-a[v[0]]);}
	db area(){return flag().len()/2;}
	db dist(point p){return fabs(((p-a[v[0]])^flag())/flag().len());}
	int see(point p){return ((p-a[v[0]])^flag())>0;}
}f[N],g[N];
int vis[N][N];
void Convex(){
	#define ft f[j].v[t]
	#define bk f[j].v[(t+1)%3]
	f[m++]=(plane){0,1,2},f[m++]=(plane){2,1,0};
	for(int i=3;i<n;i++){
		int cnt=0,b;
		for(int j=0;j<m;j++){
			if(!(b=f[j].see(a[i]))) g[cnt++]=f[j];
			for(int t=0;t<3;t++) vis[ft][bk]=b;
		}
		for(int j=0;j<m;j++)
			for(int t=0;t<3;t++)
				if(vis[ft][bk]&&!vis[bk][ft]) g[cnt++]=(plane){ft,bk,i};
		m=cnt;
		for(int j=0;j<m;j++) f[j]=g[j];
	}
} 

//Main
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=0;i<n;i++) cin>>a[i].x>>a[i].y>>a[i].z,a[i].shake();
	Convex();
	for(int i=0;i<m;i++) ans+=f[i].area()*f[i].dist(a[0])/3;
	cout.precision(2);
	cout<<fixed<<ans<<'\n';
	return 0;
}

---

祝大家学习愉快！