浅谈 Johnson 算法

目录

• 前言
• 引入
• 算法概述
  • 算法流程
  • 正确性证明
• 代码实现
• 结语

前言

Johnson 和 Floyd 一样是用来解决无负环图上的全源最短路。

在稀疏图上的表现远远超过 Floyd，时间复杂度 \(O(nm\log m)\)。

算法本身一点都不复杂（前提是你已经掌握了多种最短路算法），而且正确性很容易证明。

注意：全文多处引自SF dalao 的文章。

再次注意：模板题贴在这里，请熟读题面再看代码。

引入

想想求一个有 \(\leq 3000\) 个点和 \(\leq 6000\) 条边的有负权图的全源最短路，你发现 Floyd \(O(n^3)\) 爆体而亡。

那怎么办办呢...，我们先假设没有负权，然后可以想到一下很暴力的做法：

既然没有负权我们可以用 \(n\) 遍 dijkstra 来解决问题，复杂的 \(O(nm\log m)\)，可以接受，20pts 到手。

但是它有负权啊，你这做法有个毛线用啊

所以有一个奇怪的想法滋生在我们的脑海中：如果我们将每一个边权都加上一个定值使之为正呢？

这个想法很直接，乍一想好像还挺有道理，正在你暗暗佩服自己的睿智时，我会告诉你：这是错的。

例如对于下图：\(1\) 到 \(2\) 的最短路为 \(1\to 5\to 3\to 2\)。

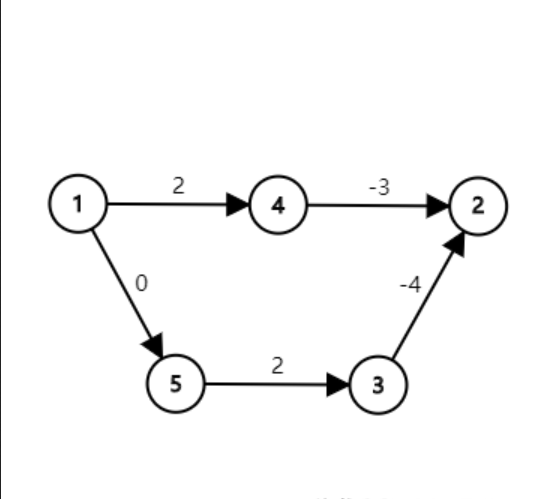
但是在所有边权加上 \(5\) 之后呢？

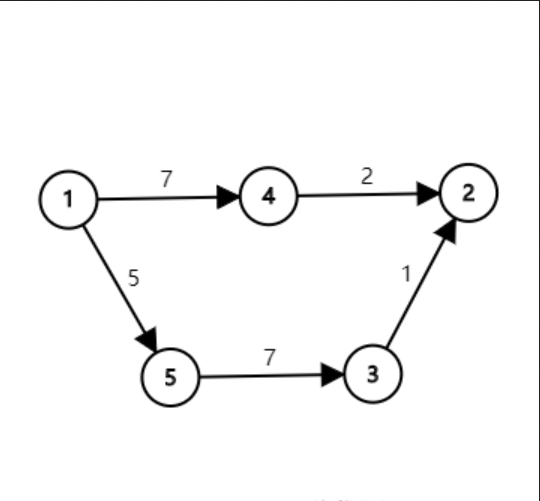
观察上图，发现最短路变成了 \(1\to 4\to 2\)，这显然是不对的。

除了有图有真相之外，我们还可以用柯学的方法来解释为什么这是错的：

因为这里的每一条路径增加的并不是一个定值。

例如这里 \(1\to 4\to 2\) 只增加了 \(10\)，而 \(1\to 5\to 3\to 2\) 却增加了 \(15\)。

显然在这种情况下，边数少的一条路径更有利，从而导致错误。

那么怎样才能使每一条路径都增加一个定值，每条边权又都变成正数呢？

这就是 Johnson 算法的核心了。

算法概述

Johnson 算法分为两步：

1. 预处理势能函数 \(h\)。（人话：跑一遍 spfa）
2. 根据势能函数求解全源最短路。（人话：跑 \(n\) 遍 dijkscal）

算法流程

这里先介绍算法流程再介绍正确性，第一遍阅读时能读懂多少就读懂多少，看完下面的证明后再回头看一眼即可。

我们新建一个虚拟节点（在这里我们就设它的编号为 \(0\)），从这个点向其他所有点连一条边权为 \(0\) 的边。

接下来用 Bellman-Ford 算法（spfa 的弱化版）求出从 \(0\) 号点到其他所有点的最短路，记为 \(h_i\)。

假如存在一条从 \(u\) 点到 \(v\) 点，边权为 \(w\) 的边，则我们将该边的边权重新设置为 \(w+h_u-h_v\)。

接下来以每个点为起点，跑 \(n\) 轮 dijkstra 算法即可求出任意两点间的最短路了。

容易看出，该算法的时间复杂度是 \(O(nm\log m)\)。

正确性证明

为什么这样重新标注边权的方式是正确的呢？

提醒一下，本文采用通俗易懂的寓言来描述证明过程，势能什么的还是参考其他人的文章吧。

咳咳，回归正题，为什么这样重新标注边权的方式是正确的呢？

假设重新标记后，\(s\) 到 \(t\) 的路径为 \(s\to p_1\to p_2\to ...\to p_k\to t\)。

那么加权之后的长度表达式为：

\((w(s,p_1)+h_s−h_{p1})+(w(p_1,p_2)+h_{p1}−h_{p2})+⋯+(w(p_k,t)+h_{pk}−h_t)\)

化简后得到：

\(w(s,p_1)+w(p_1,p_2)+ \dots +w(p_k,t)+h_s-h_t\)

那么显然，无论从那个方向走来，\(h_s-h_t\) 始终不变，变化的仅仅是路径上的边权。

即我们引言中的第一个要求：每一条路径都增加一个定值。

接下来我们需要证明新图中所有边的边权非负，因为在非负权图上，dijkstra 算法能够保证得出正确的结果。

根据三角形不等式，新图上任意一边 \((u,v)\) 上两点满足： \(h_v \leq h_u + w(u,v)\)。

这条边重新标记后的边权为 \(w'(u,v)=w(u,v)+h_u-h_v \geq 0\)。这样我们证明了新图上的边权均非负。

至此，我们就证明了 Johnson 算法的正确性。

代码实现

代码实现还是挺简单的，就不做过多介绍了。

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cmath>
#include<queue>
#include<cstdlib>
#define N 30010
#define M 60010
#define INF 1000000000
using namespace std;

int n,m,head[N],cnt=0,sum[N];
long long h[N],dis[N];
bool vis[N];
struct Edge{
	int nxt,to,val;
}ed[M];

int read(){
	int x=0,f=1;char c=getchar();
	while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
	while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
	return x*f;
}

void add(int u,int v,int w){
	ed[++cnt].nxt=head[u];
	ed[cnt].to=v,ed[cnt].val=w;
	head[u]=cnt;
	return;
}

void spfa(){
	queue<int>q;
	memset(h,63,sizeof(h));
	memset(vis,false,sizeof(vis));
	h[0]=0,vis[0]=true;q.push(0);
	while(!q.empty()){
		int u=q.front();q.pop();
		if(++sum[u]>=n){
			printf("-1\n");exit(0);
		}
		vis[u]=false;
		for(int i=head[u];i;i=ed[i].nxt){
			int v=ed[i].to,w=ed[i].val;
			if(h[v]>h[u]+w){
				h[v]=h[u]+w;
				if(!vis[v]) q.push(v),vis[v]=true;
			}
		}
	}
	return;
}

void dijkstra(int s){
	priority_queue<pair<long long,int> >q;
	for(int i=1;i<=n;i++)
		dis[i]=INF;
	memset(vis,false,sizeof(vis));
	dis[s]=0;
	q.push(make_pair(0,s));
	while(!q.empty()){
		int u=q.top().second;q.pop();
		if(vis[u]) continue;
		vis[u]=true;
		for(int i=head[u];i;i=ed[i].nxt){
			int v=ed[i].to,w=ed[i].val;
			if(dis[v]>dis[u]+w){
				dis[v]=dis[u]+w;
				if(!vis[v]) q.push(make_pair(-dis[v],v));
			}
		}
	}
	return;
}

int main(){
	n=read(),m=read();
	int u,v,w;
	for(int i=1;i<=m;i++)
		u=read(),v=read(),w=read(),add(u,v,w);
	for(int i=1;i<=n;i++)
		add(0,i,0);
	spfa();
	for(int u=1;u<=n;u++)
		for(int j=head[u];j;j=ed[j].nxt)
			ed[j].val+=h[u]-h[ed[j].to];
	for(int i=1;i<=n;i++){
		dijkstra(i);
		long long ans=0;
		for(int j=1;j<=n;j++){
			if(dis[j]==INF) ans+=(long long)j*INF;
			else ans+=(long long)j*(dis[j]+h[j]-h[i]);
		}
		printf("%lld\n",ans);
	}
	return 0;
}

结语

例题比较难找，之后遇到了会继续 Update 的，同时希望同学们遇到 Johnson 的题目及时私信告诉我。

注意：全文多处引自SF dalao 的文章。

完结撒花