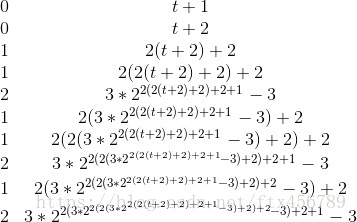牛客网多校第4场 A.Ternary String 【欧拉降幂】
题目:戳这里
学习博客:戳这里
欧拉函数的性质:
① N是不为0的整数。φ(1)=1(唯一和1互质的数就是1本身)
② 除了N=2,φ(N)都是偶数.
③ 小于N且与N互质的所有数的和是φ(n)*n/2。
④ 欧拉函数是积性函数——若m,n互质,φ(m*n)=φ(m)*φ(n)。
⑤ 当N为奇数时,φ(2*N)=φ(N)
⑥ 若N是质数p的k次幂,φ(N)=p^k-p^(k-1)=(p-1)p^(k-1),因为除了p的倍数外,其他数都跟N互质。
⑦ 当N是质数时,φ(N) = N-1
广义欧拉定理:
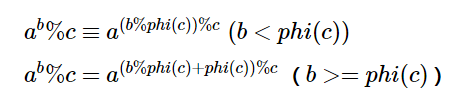
题意和解题思路见上面的学习博客
重点图:
通过这题的计算我们可以发现,对于任何模的欧拉降幂都是可以直接预处理的。
因为phi(1) = 1,而1e9 + 7递归求的phi才28个。
1 #include<iostream>
2 #include<algorithm>
3 #include<stdio.h>
4 #include<string.h>
5 #include<string>
6 #include <cmath>
7 using namespace std;
8 typedef long long ll;
9 const ll mod = 1e9 + 7;
10 const int maxn = 2e5 + 10;
11 char s[maxn];
12 ll qmul(ll a, ll b, ll m)
13 {
14 ll ans = 0;
15 while(b)
16 {
17 if(b & 1)
18 ans = (ans + a) % m;
19 b >>= 1;
20 a = (a + a) % m;
21 }
22 return ans;
23 }
24 ll qmod(ll a, ll b, ll m)
25 {
26 ll ans = 1;
27 while(b)
28 {
29 if(b & 1)
30 ans = qmul(ans, a, m) % m;
31 b >>= 1;
32 a = qmul(a, a, m) %m;
33 }
34 return ans;
35 }
36 ll phi(ll x)
37 {
38 ll i, res = x;
39 for(i = 2; i < sqrt(x * 1.0) + 1; ++i)
40 {
41 if(!(x % i))
42 {
43 res = res / i * (i - 1);
44 while(!(x % i))
45 {
46 x /= i;
47 }
48 }
49 }
50 if(x > 1)
51 res = res / x * (x - 1);
52 return res;
53 }
54 ll p[33];
55 int main()
56 {
57 p[0] = p[1] = mod;
58 int cnt = 0;
59 for(int i = 2;; ++i)
60 {
61 p[i] = phi(p[i - 1]);
62 if(p[i] == 1)
63 {
64 cnt = i;
65 break;
66 }
67 }
68 int t;
69 scanf("%d", &t);
70 while(t--)
71 {
72 int n;
73 scanf("%s", s);
74 n = strlen(s);
75 int num = 0;
76 int pos = 0;
77 for(int i = n - 1; i >= 0; --i)
78 {
79 if(s[i] == '2')
80 ++num;
81 if(num == 28)
82 {
83 pos = i;
84 break;
85 }
86
87 }
88 ll ans = 0;
89 ++num;
90 for(int i = pos; i < n; ++i)
91 {
92 if(s[i] == '0')
93 ans = (ans + 1) % p[num];
94 if(s[i] == '1')
95 ans = (2 * ans % p[num] + 2 % p[num]) % p[num];
96 if(s[i] == '2')
97 {
98 --num;
99 ans = (3 % p[num] * qmod(2, ans + 1, p[num])) % p[num];
100 ans = (ans % p[num] - 3 + p[num]) % p[num];
101 }
102 }
103 printf("%lld\n", ans % mod);
104 }
105
106 }
牛客网多校第4场 A.Ternary String 【欧拉降幂】的更多相关文章
- 牛客网多校第3场Esort string (kmp)
链接:https://www.nowcoder.com/acm/contest/141/E 来源:牛客网 题目描述 Eddy likes to play with string which is a ...
- 牛客网多校第3场C-shuffle card 平衡树或stl(rope)
链接:https://www.nowcoder.com/acm/contest/141/C 来源:牛客网 题目描述 Eddy likes to play cards game since there ...
- 牛客网多校赛第九场A-circulant matrix【数论】
链接:https://www.nowcoder.com/acm/contest/147/A 来源:牛客网 时间限制:C/C++ 1秒,其他语言2秒 空间限制:C/C++ 262144K,其他语言524 ...
- 牛客网多校训练第二场D Kth Minimum Clique
链接:https://ac.nowcoder.com/acm/contest/882/D来源:牛客网 Given a vertex-weighted graph with N vertices, fi ...
- 牛客网多校第5场 H subseq 【树状数组+离散化】
题目:戳这里 学习博客:戳这里 题意:给n个数为a1~an,找到字典序第k小的序列,输出该序列所有数所在位置. 解题思路:先把所有序列预处理出来,方法是设一个数组为dp,dp[i]表示以i为开头的序列 ...
- 牛客网多校第5场 I vcd 【树状数组+离散化处理】【非原创】
题目:戳这里 学习博客:戳这里 作者:阿狸是狐狸啦 n个点,一个点集S是好的,当且仅当对于他的每个子集T,存在一个右边无限延长的矩形,使的这个矩形包含了T,但是和S-T没有交集. 求有多少个这种集合. ...
- 牛客网多校第4场 J Hash Function 【思维+并查集建边】
题目链接:戳这里 学习博客:戳这里 题意: 有n个空位,给一个数x,如果x%n位数空的,就把x放上去,如果不是空的,就看(x+1)%n是不是空的. 现在给一个已经放过数的状态,求放数字的顺序.(要求字 ...
- 2018牛客网暑期ACM多校训练营(第四场) A - Ternary String - [欧拉降幂公式][扩展欧拉定理]
题目链接:https://www.nowcoder.com/acm/contest/142/A 题目描述 A ternary string is a sequence of digits, where ...
- 牛客网多校训练第一场 J - Different Integers(树状数组 + 问题转换)
链接: https://www.nowcoder.com/acm/contest/139/J 题意: 给出n个整数的序列a(1≤ai≤n)和q个询问(1≤n,q≤1e5),每个询问包含两个整数L和R( ...
随机推荐
- 30分钟带你理解 Raft 算法
为什么需要 Raft? Raft 是什么? Raft 的目标 前置条件:复制状态机 Raft 基础 Leader 选举(选举安全特性) 日志复制(Leader只附加.日志匹配) 安全 学习资料 使用 ...
- Linux学习安装
Linux学习安装 服务器指的是网络中能对其他机器提供某些服务的计算机系统,相对普通PC, 服务器指的是高性能计算机,稳定性.安全性要求更高 linux安装学习 1.虚拟机 一台硬件的机器 安装vmw ...
- cfsetispeed、cfsetospeed和cfsetspeed探究
在我https://www.cnblogs.com/Suzkfly/p/11055532.html这篇博客中有一个疑问,就是在串口设置波特率的域中,没有将输入输出波特率分开,那为什么会有几个不同的设置 ...
- ES入门及安装软件
es介绍 Elasticsearch,简称es,是一款高扩展的分布式全文检索引擎.它可以近乎实时的存储,检索数据.es是面向文档型的数据库,一条数据就是一个文档,用json做为文档序列化的格式.es是 ...
- There are only two hard things in Computer Science: cache invalidation and naming things.
TwoHardThings https://martinfowler.com/bliki/TwoHardThings.html https://github.com/cch123/golang-not ...
- python_3 装饰器之初次见面
装饰器 定义:本质是函数,(只不过是用来装饰其他函数而已),就是为其他函数添加附加功能 原则: 1. 不能修改被修饰函数的源代码 2.不能修改被修饰函数的调用方式 实现装饰器的知识储备 1.函数即&q ...
- LOJ10090
题目描述 原题来自:USACO 2005 Dec. Gold FJ 有 n 头奶牛(2<=n<=1000) ,编号为1..n .奶牛们将按照编号顺序排成一列队伍(可能有多头奶牛在同一位置上 ...
- 利用burp抓取https的包
本片文章仅供学习使用,切勿触犯法律! 0x01.打开burp的代理监听器 0x02.使用代理访问 这里我是用的是mantra,其他浏览器同理. 0x03.浏览器输入http://burp 点击CA C ...
- vue项目在IE下报 [vuex] vuex requires a Promise polyfill in this browser错误
ie浏览器下报错 vue刚搭建的项目,在谷歌浏览器能够正常访问,但是在ie11等ie浏览器下无法显示页面,打开控制台查看无报错信息,打开仿真一栏,提示[vuex] vuex requires a Pr ...
- Java——介绍
Java基础语法: 一个Java程序可以认为是一系列对象的集合,而这些对象通过彼此的方法来协同工作. 对象: 对象是类的一个实例,有状态和行为.例如,一条狗是一个对象,它的状态有:颜色.名字.品种:行 ...