hdu1828 Picture(线段树+扫描线+矩形周长)

看这篇博客前可以看一下扫描线求面积：线段树扫描线（一、Atlantis HDU - 1542（覆盖面积） 二、覆盖的面积 HDU - 1255（重叠两次的面积）） 

解法一·：两次扫描线

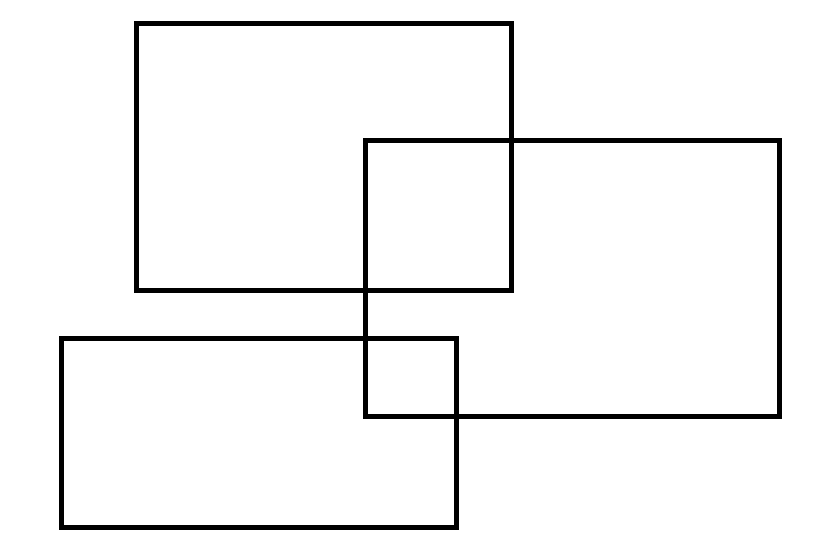
如图我们可以先用扫描线找出来横线的周长和，再用扫描线找纵线周长和

这里以横线来举例：

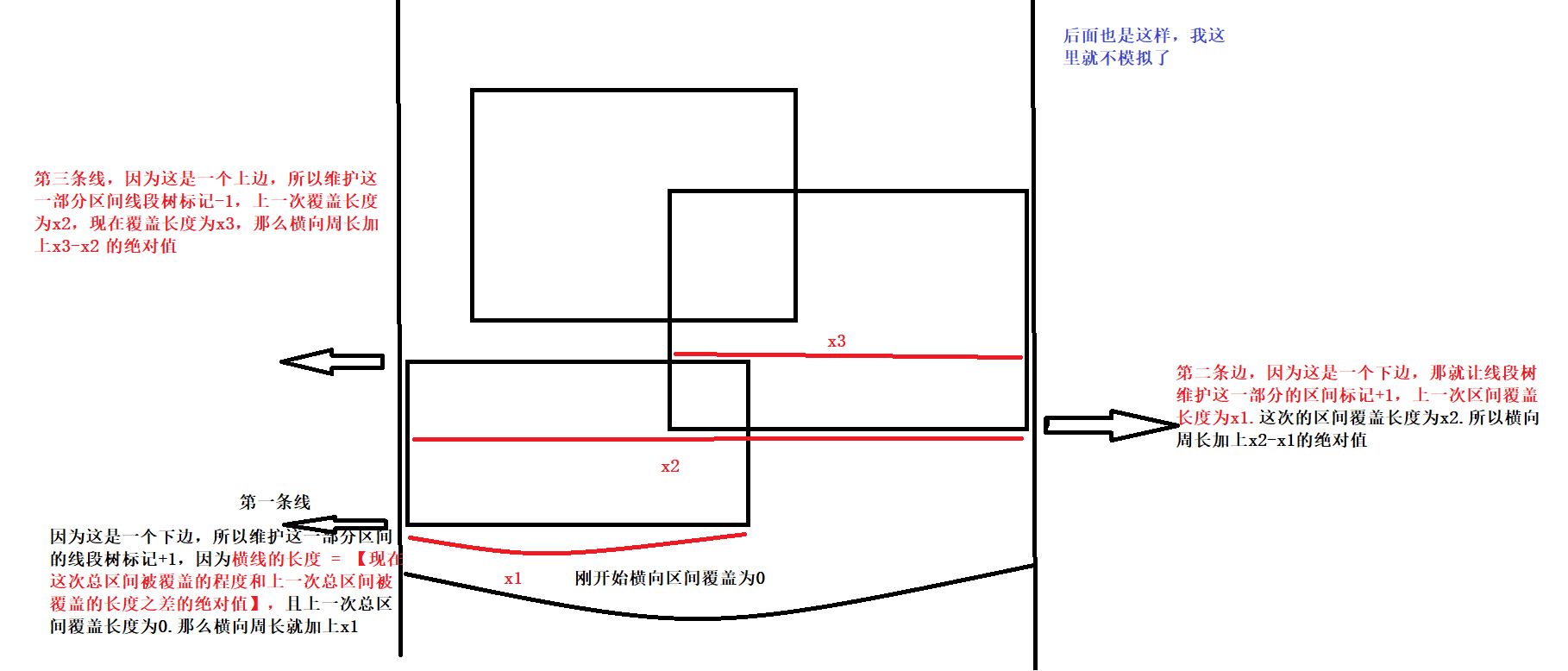
横线的长度 = 【现在这次总区间被覆盖的程度和上一次总区间被覆盖的长度之差的绝对值】

下面有一点要注意的（参考链接：https://www.cnblogs.com/violet-acmer/p/11461660.html）

需要注意的是，在求解矩形面积并的时候，排序策略是按照 h 从小到大排序，并不需要考虑 h 相同的情况；
但是求矩形周长并的时候就不行了，必须得考虑 h 相同的情况下的排序策略；
以下例求解横线并的长度为例；
　　　　n=2
　　　　(2,1),(4,3)
　　　　(3,3),(4,5)

假设与处理矩形面积并的排序策略相同，只考虑按 h 升序排列，那么排列后的数据为：
　　　　e1:{l=2 , r=4 , h=1 , f=1}e1:{l=2 , r=4 , h=1 , f=1}
　　　　e2:{l=2 , r=4 , h=3 , f=−1}e2:{l=2 , r=4 , h=3 , f=−1}
　　　　e3:{l=3 , r=4 , h=3 , f=1}e3:{l=3 , r=4 , h=3 , f=1}
　　　　e1:{l=3 , r=4 , h=5 , f=−1}e1:{l=3 , r=4 , h=5 , f=−1}
　　让我们手动模拟一下这个求解过程；
　　定义 ans 表示答案，len 表示当前更新后的横线并的总长度，pre 表示上一次更新后的 len 值；
　　初始化 ans=0,len=0,pre=0;
　　首先处理 e1e1，update() 后，len = 2;
　　更新 ans += |len-pre| = 2 , pre=len=2;
　　处理 e2e2，update() 后，len = 0;
　　此时，更新 ans += |len-pre| = 2+2 = 4 , pre=len=0，出现问题了是吧，因为来到此处的时候，ans=3才对；
　　继续向上更新， e3e3，update() 后，len=1;
　　更新 ans += |len-pre| = 4+1 = 5 , pre=len=1;
　　e4e4，update() 后，len=0；
　　更新 ans += |len-pre| = 5+1 = 6；
　　但是正确答案应该是 ans = 4；
　　多的 2 就是因为排序策略不当而产生的；
　　所以，当 h 相同的时候，应该先处理 f = 1 的边，即如果可以先加入边，那就优先执行加边操作；

第二种解法：参考：https://blog.csdn.net/qq3434569/article/details/78220821

看出什么了吗？这张图在上面那张图的基础上多了几条竖线。

我的意思是说，我们可以只做一次自下而上的扫描就把横线竖线都算出来！

竖线的算法和上面说的方法一样：【现在这次总区间被覆盖的程度和上一次总区间被覆盖的长度之差的绝对值】

竖线要怎么计算？

首先我们现在改一下线段树保存的属性，我们用如下信息记录线段树的节点：

1. l , r : 该节点代表的线段的左右端点坐标

2.len : 这个区间被覆盖的长度（即计算时的有效长度）

3.s : 表示这个区间被覆盖了几次

4. lc , rc : 标记这个节点的左右两个端点是否被覆盖（0表示没有，1表示有）

5.num :这个区间有多少条线段（这个区间被多少条线段覆盖）

这里的num涉及到竖线的计算，故解释一下,举几个例子：

若区间[0,10]被[1,2][4,5]覆盖，则num = 2

若区间[0,10]被[1,3][4,5]覆盖，则num = 1（两区间刚好连在一起）

若区间[0,10]被[1,5][2,6]覆盖，则num = 1（两区间连起来还是一段）

然后就可以计算竖线了：

竖线的长度 = 【下一条即将被扫到的横线的高度 - 现在扫到的横线的高度】*2*num

乘2是因为每条线段有两个端点；

看上图中棕色线段的竖线有4条，因为棕色的横线由2条线段组成

白色线段的竖线只有2条，因为白色的横线由1条线段组成（虽然这1条线段是由许多线段组合而成，但它依旧只算1条线段）

这样，依旧只扫一次就可以算出周长。

本题用第二种方法写的代码：

 1 #include <cstdio>
 2 #include <cstring>
 3 #include <cctype>
 4 #include <algorithm>
 5 using namespace std;
 6 #define lson l , m , rt << 1
 7 #define rson m + 1 , r , rt << 1 | 1
 8 const int maxn = 22222;
 9 struct Seg
10 {
11     int l, r, h, s;
12     Seg() {}
13     Seg(int a, int b, int c, int d) :l(a), r(b), h(c), s(d) {}
14     bool operator < (const Seg &cmp) const
15     {
16         return h < cmp.h;
17     }
18 } ss[maxn];
19 bool lbd[maxn << 2], rbd[maxn << 2];//标记这个节点的左右两个端点是否被覆盖（0表示没有，1表示有）
20 int numseg[maxn << 2];//这个区间有多少条线段（这个区间被多少条线段覆盖）
21 int cnt[maxn << 2];//表示这个区间被重复覆盖了几次
22 int len[maxn << 2];//这个区间被覆盖的长度
23 void PushUP(int rt, int l, int r)
24 {
25     if (cnt[rt])  //整个区间被覆盖
26     {
27         lbd[rt] = rbd[rt] = 1;
28         len[rt] = r - l + 1;
29         numseg[rt] = 2;//每条线段有两个端点
30     }
31     else if (l == r)  //这是一个点而不是一条线段
32     {
33         len[rt] = numseg[rt] = lbd[rt] = rbd[rt] = 0;
34     }
35     else  //是一条没有整个区间被覆盖的线段，合并左右子的信息
36     {
37         lbd[rt] = lbd[rt << 1]; // 和左儿子共左端点
38         rbd[rt] = rbd[rt << 1 | 1]; //和右儿子共右端点
39         len[rt] = len[rt << 1] + len[rt << 1 | 1];
40         numseg[rt] = numseg[rt << 1] + numseg[rt << 1 | 1];
41         if (lbd[rt << 1 | 1] && rbd[rt << 1]) numseg[rt] -= 2;//如果左子的右端点和右子的左端点都被覆盖了即两条线重合
42     }
43 }
44 void update(int L, int R, int c, int l, int r, int rt)
45 {
46     if (L <= l && r <= R)
47     {
48         cnt[rt] += c;
49         PushUP(rt, l, r);
50         return;
51     }
52     int m = (l + r) >> 1;
53     if (L <= m) update(L, R, c, lson);
54     if (m < R) update(L, R, c, rson);
55     PushUP(rt, l, r);
56 }
57 int main()
58 {
59     int n;
60     while (~scanf("%d", &n))
61     {
62         int m = 0;
63         int lbd = 10000, rbd = -10000;
64         for (int i = 0; i < n; i++)
65         {
66             int a, b, c, d;
67             scanf("%d%d%d%d", &a, &b, &c, &d);
68             lbd = min(lbd, a);
69             rbd = max(rbd, c);
70             ss[m++] = Seg(a, c, b, 1);
71             ss[m++] = Seg(a, c, d, -1);
72         }
73         sort(ss, ss + m);
74         //数据小可以不离散化
75         int ret = 0, last = 0;
76         for (int i = 0; i < m; i++)
77         {
78             if (ss[i].l < ss[i].r) update(ss[i].l, ss[i].r - 1, ss[i].s, lbd, rbd - 1, 1);
79             ret += numseg[1] * (ss[i + 1].h - ss[i].h);//竖线的长度 = 【下一条即将被扫到的横线的高度 - 现在扫到的横线的高度】*num
80             ret += abs(len[1] - last);//横线的长度 = 【现在这次总区间被覆盖的程度和上一次总区间被覆盖的长度之差的绝对值】
81             last = len[1];//每次都要更新上一次总区间覆盖的长度
82         }
83         printf("%d\n", ret);
84     }
85     return 0;
86 }