P1962 斐波那契数列-题解（矩阵乘法扩展）

https://www.luogu.org/problemnew/show/P1962(题目传送)

n的范围很大，显然用普通O(N)的递推求F(n)铁定超时了。这里介绍一种用矩阵快速幂实现的解法：

首先普及一下矩阵乘法：

一个m*q的m行q列的矩阵A*一个q*n的q行n列的矩阵B得到一个m*n的m行n列的矩阵AB,则有:

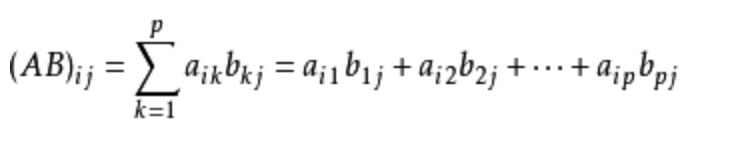
通俗的讲，就是新矩阵第i行j列的数等于第一个矩阵第i行的q个数分别乘第二个矩阵的第j列的q个数并把它们加起来的和。注意，矩阵乘法满足结合律和分配律，但不满足交换律。

我们可以把第n项F(n)、第n-1项F(n-1)写成一个1*2的矩阵[Fn  ​​Fn-1] 并考虑怎样由前面的[Fn-1  ​​Fn-2]推过来。可以先把[Fn  ​​Fn-1]写成[1*Fn-1+1*Fn-2  ​​1*Fn-1+0*Fn-2]的形式，试推导一个矩阵base，使

[Fn-1  ​​Fn-2]*base=[Fn  ​​Fn-1]=[Fn-1+Fn-2  ​​Fn-1]，因为Fn-1和Fn-2都在结果矩阵的第一列以系数为1的形式出现，结果矩阵是一个1*2的矩阵，所以base为一个2*2的矩阵，且第一列为1，1；

Fn-1和Fn-2在结果矩阵的第二列以系数为1、0的形式出现，所以结果矩阵第二列为1,0。即base= ，[Fn-1  ​​Fn-2]*=[Fn  ​​Fn-1]。

同理可以推出[Fn-2  ​​Fn-3]**=[Fn  ​​Fn-1]…………[F2 F1]*^(n-2)=[Fn Fn-1]。

此时本题的核心便是计算出base=的n-2次方就行了，可以用矩阵快速幂做（换汤不换药）

代码如下：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 using namespace std;
 const long long mod=;
 struct matrix{                    //用结构体构建矩阵类型
     long long a[][];
 }ans,a;
 int init()                        //初始化矩阵。ans存放题解中提到的1*2的矩阵，这里为了统一用同一种矩
                                 //阵乘法的处理，又发现若矩阵的一行（或一列）全为0，则乘法的结果矩阵
                                 //的对应行（或列）也全为0，不影响结果,便用0把ans扩充成2*2的矩阵了 。
 {
     ans.a[][]=ans.a[][]=;
     a.a[][]=a.a[][]=a.a[][]=;
 }
 matrix operator *(matrix a,matrix b)//矩阵乘法实现（运算符重载）
 {
     matrix c;
     for(int i=;i<=;i++)
         for(int j=;j<=;j++) c.a[i][j]=;
     for(int i=;i<=;i++)
         for(int j=;j<=;j++)
             for(int k=;k<=;k++)
             c.a[i][j]=(c.a[i][j]+a.a[i][k]*b.a[k][j])%mod;
     return c;
 }
 int main()
 {
     long long n;
     cin>>n;
     if(n<=)
     {
         cout<<;
         return ;
     }
     long long b=n-;
     init();
     while(b)                    //万年不变的快速幂
     {
         if(b&) ans=ans*a;
         a=a*a;
         b>>=;
     }
     cout<<ans.a[][];
     return ;
 }