probabilistic robotics_Kalman filter(一)

码农生活告一段落，继续。。。。

多元正态分布

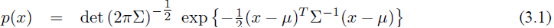
协方差矩阵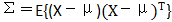，为正定对称矩阵。det表示行列式

协方差反应随机样本变量各分量之间的相关性。

当变量的假设模型不一致时，不适合用高斯滤波。

叠加高斯噪声的线性假设

联立1,2式可得状态转移概率

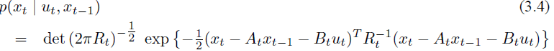
测量值

卡尔曼滤波

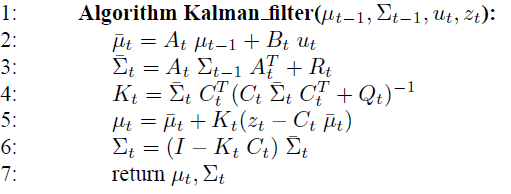
初始置信度

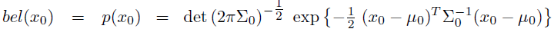
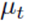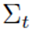1、 其中贝叶斯滤波中的后验概率bel(x)由均值和协方差表示。整个算法流程就是在对二者不停的做迭代计算。

2、 可以看出增益系数K由前验概率中的协方差以及测量系数、测量误差这三者来决定。

3、 均值的更新需要用的测量值zt，协方差的更新只与上次协方差以及本次增益系数有关。

推导过程太繁复，略过不看了。

扩展卡尔曼滤波

式3.2与3.5

由如下两式代替

1、状态转移函数以及测量概率函数由原来的线性假设变为了非线性假设，但误差还是符合正态分布。

2、但是整体的后验概率将不符合高斯分布（正态分布），用原来的贝叶斯滤波将不会有闭环解（closed-form solution），所以扩展卡尔曼滤波只能计算近似解。

3、扩展卡尔曼滤波通过对函数的泰勒展开来逼近线性函数。

泰勒展开

偏导公式：

在上一次的均值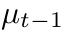处对做泰勒展开有：

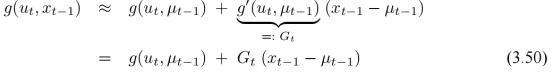
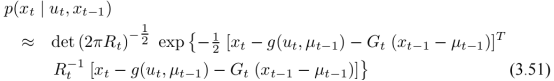
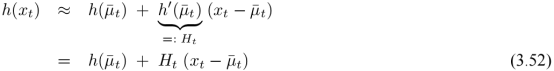
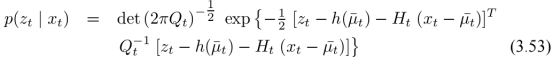
算法描述

对比KF，可以发现原来的A、B、C由G、H代替。

实际考虑

1、多模型考虑。有时候，会用到多个模型对状态进行估计，这些模型没有相互冲突。此时可采用对模型加权的方式进行处理。称为多假设（扩展）卡尔曼滤波（Multi-Hypthesis (Extended) Kalman Filter,MHEKF），其中的加权系数为似然估计。

2、局部非线性化，局部线性化程度高，泰勒展开越逼近真实结果，滤波效果越好。

3、不确定性（方差），当状态的不确定性（方差）很大时，经过非线性函数的变换，结果容易扩散，得到的概率密度函数更加扭曲。

4、比之泰勒展开更加高级的另两种方式，一种是无迹卡尔曼滤波（Unscented KF,UKF）,它通过使用加权统计线性回归过程实现随机线性化（机器学习）；另一种是矩匹配（moments mathching）,它仅通过对后验分布的真实均值与方差来计算。

下一步将用matlab进行模拟。