Andrew Ng机器学习笔记

Week_3 -- -Logistic Regression

This week, we’ll be covering logistic regression. Logistic regression is a method for classifying data into discrete outcomes. In this module, we introduce the notion of classification, the cost function for logistic regression, and the application of logistic regression to multi-class classification.

We’ll introduce regularization, which helps prevent models from over-fitting the training data.

1.Classification

例子：肿瘤与否，垃圾邮件与否

一般可以通过Threshold,阈值，来辨别

例如：０和１的话，可以选择0.5作为阈值

和回归问题差不多，不过这个数据是离散数据

For Now,we will focus on the Binary Classification Problem

in which you can take on only two values, 0 and 1. (Most of what we say here will also generalize to the multiple-class case.)

例如：识别垃圾邮件的时候，我们用$x^{(i)}$　来表示垃圾邮件的特征量feature, Y则只有２个值，１和０，表示是垃圾邮件和非垃圾邮件。

2.Hypothesis Representation假设函

讨论逻辑函数的假设函数----逻辑回归

首先我们需要的假设函数应该预测值在０到１之间

模仿线性回归的形式：　

\[h_\theta(x) = g(\theta^T X)
\]

其中定义g(Z) = $\frac1{1+e^{-z}}$

即是：$h_\theta(x) = \frac1{1+e^{\theta^T x}}$

如下图：

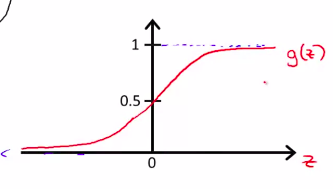
这可以理解为一个概率函数

可以写为　　　$h_\theta(x) = {(y = 1 | x,\theta)}$

概率参数为$\theta$和ｘ,y只有１或者０　。值就是有肿瘤的概率(1)

3. Decision Boundary 决策界限

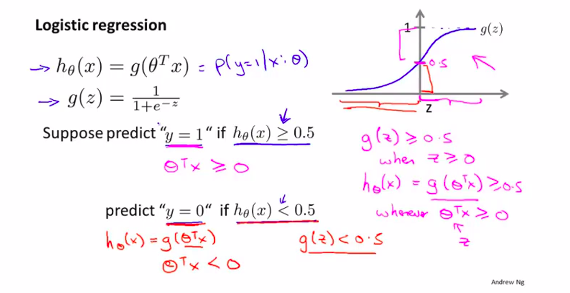
如上图所示：0.5即为决策界限

那么如何算出　决策界限呢？

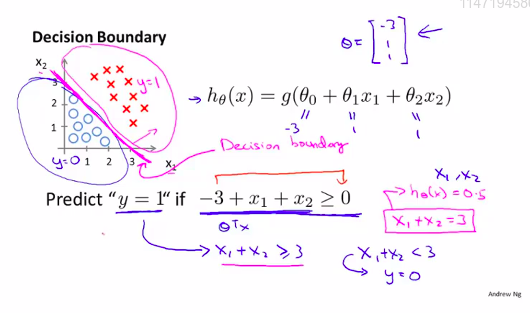
上面是线性的，那么，非线性拟合呢？

那就要通过增加参数\theta

5. 优化目标，代价函数cost function

目标：如何拟合$\theta$??

和线性回归的代价函数相似：

定义：$J(\theta) = \frac1m\sum_{i=1}^mCost(h_\theta(x),y)$

其中Cost 函数可以等于　$\frac12(h_\theta(x) - y)^2$

但是，在classification 中，h（x）是非线性的,所以，h(x)图像可能为：

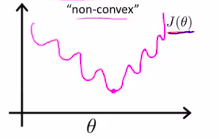
所以，根据ｈ（ｘ）的定义

可以定义cost函数

它的图像为：

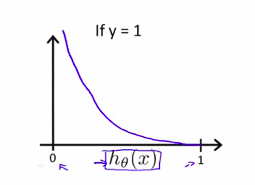
J(\theta)将会是一个凸函数且没有局部最优

6.更简单的方式找到代价函数.用梯度下降来拟合逻辑回归的参数$\theta$.Simplified Cost Function and Gradient Descent

代价函数可以不用分段函数：还可以用

$Cost(h_\theta(x),y) = -yln(1 - h_\theta(x)) - (1-y)ln(1-h_\theta(x))$

来表示，这样就不用分段了

所以，代价函数就是：

或者，用向量来表示：

类似，我们要找到Ｊ（$\theta $）的最小值

当然，使用Gradient Descent梯度下降

如图操作，注意此时ｈ函数不是和线性回归的是一样的

接下来，如何监测梯度下降？

当然，也可以用向量方法来实现：？？？？？（如何推导？？）

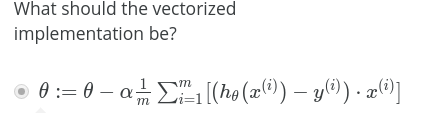
看这里更清楚：（截图功能真的是太赞了！）

7.高级优化Advanced Optimization

算法优化，Optimization algorithms

Gradient descent
Conjugate gradient
BFGS
L-BFGS 共轭梯度算法

后三种算法的优点：

No need to manually pick $\alpha$
Often faster than gradient descent

缺点：

More complex

代码细节不用知道！

可以以后学习tensorflow 来实现

8. Multiclass classification

例如，把邮件贴上不同的标签

那么，如何找到多元分类的决策界限？

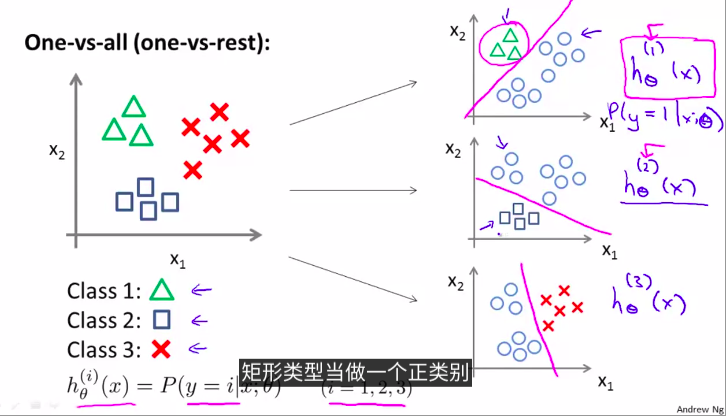
例如，3种的话，通过两两分类

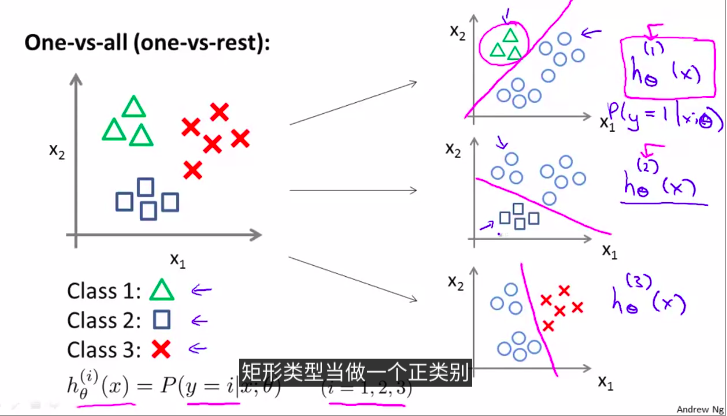
一对多方法。分为3个二元问题

上图拟合出3个分类器

$h_\theta^{(i)}(x) = P(y = i| x,\theta), (i = 1,2,3)$

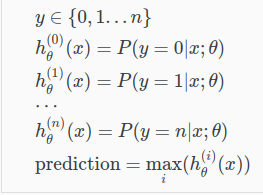
9. 过度拟合的问题over-fitting

变量太多，无法通过更多的数据来进行约束

以至于无法泛化到新数据中

线性：

第一个是under fitting ,欠拟合,有 high bias

第二个just right

第三个则是over fitting

逻辑回归：

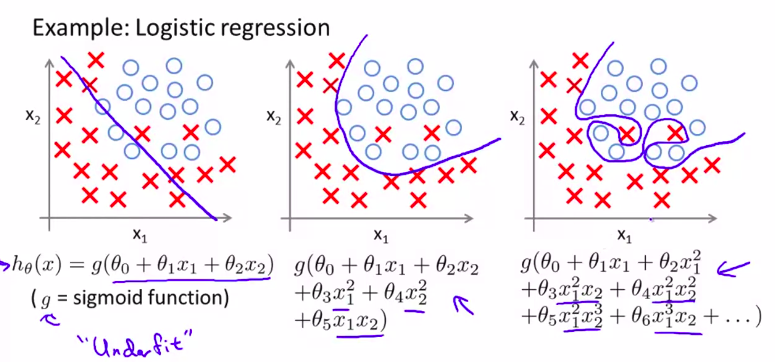
如何解决？

减少变量数目 reduce number of features
Regularization正则化

10. Regularization and its Cost function 正则化及其代价函数

像上节课一样，当过度拟合的时候，我们可以让其他的参数的影响尽可能的小

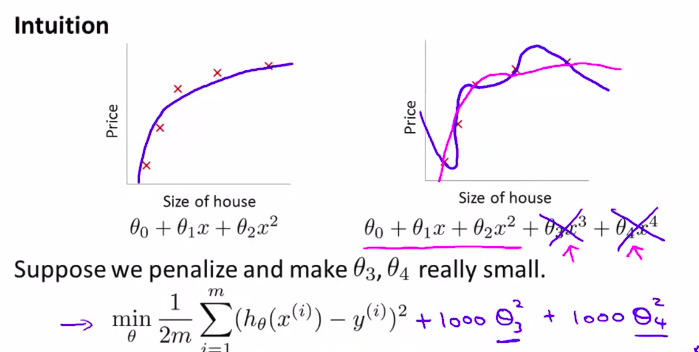
penalize惩罚$\theta_3和\theta_4$这两个参数。使他们尽可能为0

如何操作？

在最初的cost function中添加正则化项

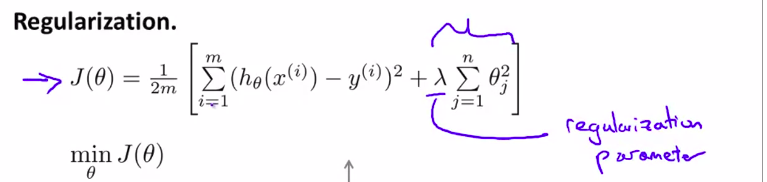
$\lambda$ 叫做正则化参数

$\lambda $太大的话，会under fitting

所以应该选择合适的正则化参数

一张图来解释：

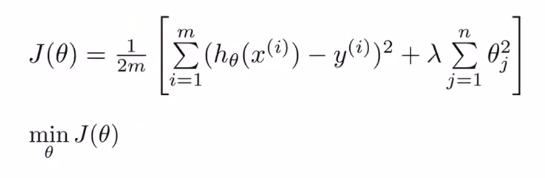
11. 正则线性回归Regularized Linear Regression

算法：

Gradient descent

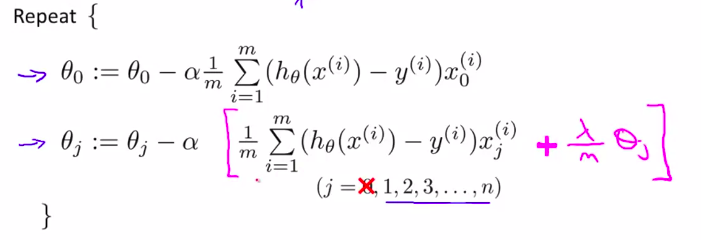
可以等价的写为：

$\theta_j := \theta_j(1- \alpha\frac1m) - \alpha\frac1m\sum_{i=1}^m(h_\theta(x^{(i)}_j)-y^{(i)}) x_j^{(i)}$

其中$1-\alpha\frac1m$这一项，如果学习率小，例子数量大的化，一般是比1小于一点点的值

而后面这一大坨，则和以前一模一样！！！

只不过前面这一项把theta压缩了！

Normal equation

使用了正则化，如何得到矩阵式子？

数学推导略！

或者写成：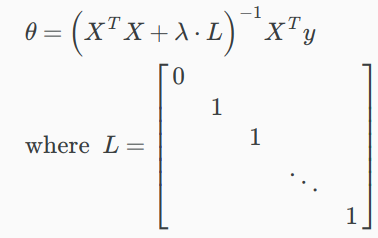

12. Regularized Logistic Regression 逻辑回归的正则化

和线性回归差不多，要添加正则项

算法类似，都要将0单独写出

下面来说明如何在更高级的算法中，应用正则化：

（学完octave后，应该就能看懂）

综上所述：

题目摘录：

第 3 题

Which of the following statements about regularization are true? Check all that apply.

Using too large a value of λ can cause your hypothesis to overfit the data; this can be avoided by reducing λ.

Using a very large value of λ cannot hurt the performance of your hypothesis; the only reason we do not set λ to be too large is to avoid numerical problems.

Consider a classification problem. Adding regularization may cause your classifier to incorrectly classify some training examples (which it had correctly classified when not using regularization, i.e. when λ=0).

Because logistic regression outputs values 0≤hθ(x)≤1, its range of output values can only be “shrunk” slightly by regularization anyway, so regularization is generally not helpful for it.

```
答案: 3 *
```

正则化方法的公式: J(θ)=12m[∑i=1m(hθ(x(i))−y(i))2+λ∑i=1nθ2j]J(θ)=12m[∑i=1m(hθ(x(i))−y(i))2+λ∑i=1nθj2]

选项1: λλ太大导致overfit不对,是underfit,当λλ太大时θ1θ2...θn≈0θ1θ2...θn≈0.只有θ0θ0起作用,拟合出来是一条直线. λλ太小才会导致overfit. 不正确 **
选项2: 同1. 不正确 **
选项3: 当λλ没有选择好时,可能会导致训练效果还不如不加的λλ好. 正确 **
选项4: “shrunk” slightly的是θθ, regularization是想要解决overfit. 不正确！

第 1 题

You are training a classification model with logistic

regression. Which of the following statements are true? Check

all that apply.

Introducing regularization to the model always results in equal or better performance on the training set.

Adding many new features to the model helps prevent overfitting ont the training set.

Introducing regularization to the model always results in equal or better performance on examples not in the training set.

Adding a new feature to the model always results in equal or better performance on the training set.

```
答案: 4 *
```