SAM复杂度证明

关于$SAM$的复杂度证明(大部分是对博客的我自己的理解和看法)

这部分是我的回忆,可省略

先回忆一下$SAM$

我所理解的$SAM$,首先扒一张图

初始串$aabbabd$

首先发现,下图里的$S->9$的一条直线是$aabbabd$是原串

那么从这里我们就可以看到$endpos$关系了,和$AC$自动机不同的是

发现一些子串结尾是相同的,那么就可以共用一个节点,那么从起点到这个点能表示的所有子串的$endpos$相同,那么显然可以共用这个点,这就是空间上的能省就省

又因为这个$SAM$是为了表示所有的子串或者后缀,那么$endpos$相同的话,也就是说在这个状态结束之后都会在这个点继续向后延伸

先粗糙的理解一下,那我们是不是可以理解为,我们要插入一个后缀,那么需要节省空间吧,那么如果一个以他为结尾的点,在多个子串里经过,那么就可以多次使用这个点

那么就拿下图的$4$举例,前面有三个满足条件(下面解释)的后缀有三个,那么这个节点可以被使用三次在三个后缀里

这个$4$节点表示的$endpos$也仅仅只是只是$endpos=4$

还是举例$ab$这个后缀为什么没在$S->7$的某条路径上,其实本应该出现的,发现这时$ab$在$S->8$的路径上,这个被分出来了,为何,因为这时$endpos(ab)!=7,$应该出现是因为他的$endpos$有$7$,没有出现是因为这是一个新的类型,如果归成一类的话,就无法满足经过这个之后统一在这个点出去了,那么只能自成一家

虽然自成一家了,也不是毫无关系,毕竟$endpos$集合有重复的部分,那么显然的,这个$endpos$集合是一个有序的,就是递增的,那么在一个串是另一个串后缀的时候,越短的串的$endpos$越大,而且大的集合必然包含小的集合,那么这个东西就是可以通过一个指向关系来确定了

转移边也是相当于$AC$自动机的转移边,就是这个$endpos$集合能到达的下个$endpos$集合,上文说了,我们把所有仅在这个点结束的统一放一起,那么可以在这里统一出发向能到达的所有$endpos$去转移

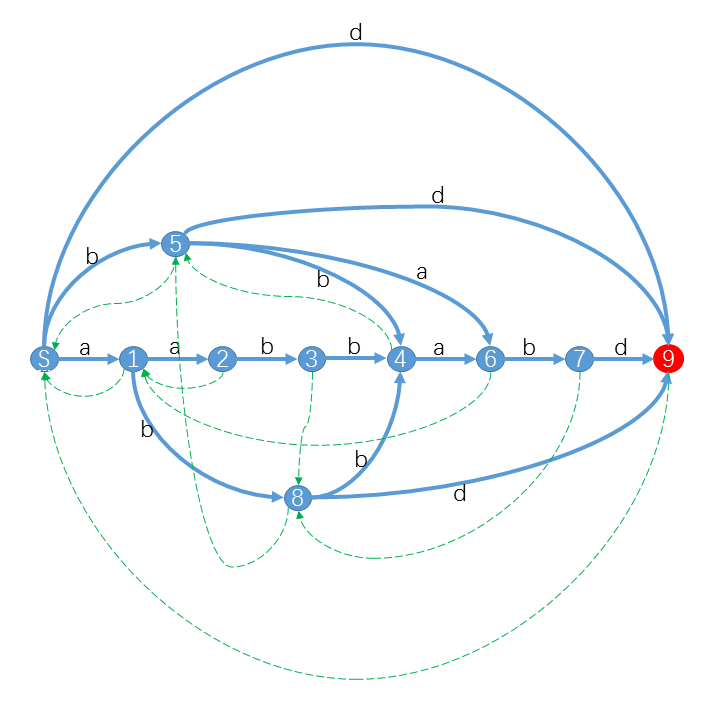
上面说的这些,到这里汇总一下,思考这个东西是如何构造的

找出所有后缀一个个插入$ \xcancel{\huge NO} $

增量法构造$\checkmark $

在增量的过程中思考一下复杂度

首先明确我们在自动机维护什么,修改时改变什么

维护$len_{max},len_{min},trans,link$

这个东西肯定在遍历$SAM$没啥用,那么我们可以用这几个东西快速找到插入点

构造自动机,假设我们目前插入$S_k$

我们建完了前面的自动机,需要加一个字符,也就是需要表示的字符多了$k-1$个,就是所有包含最后一个字符的子串

首先在后缀自动机上多一个节点,表示$endpos=k$,显然的,从大到小的所有新增字符串,首先,最大的$endpoz=k$,那么小的字符串的$endpos$可能不仅仅是$k$,可能在前面也出现了,在自动机上的体现就是一个节点的$tran[now][s[k]]!=0$,也就是说这个后缀曾经被表示了,这个时候看看上面的需要改变的部分,首先这个被表示的后缀的$endpos$发生了变化,多了一个位置,那么这个状态其他的如果没变的话,就需要把这个状态分开了,上面证明,越长的串$endpos$越小,那么会分成两部分,变的和不变的,注意$!$这个时候插入一个串要么增加一个节点,要么不变,不会再增加更多节点了,那么我们需要解决的仅仅是在跳跃找的时候的复杂度了(说实话,这个我没仔细看过...)

时间复杂度和你每次添加新字符多的状态数和需要跳几次有关

上文证明了,状态数$O(2\times n)$

放一份代码

//回顾
//Link一个字符串所有后缀变换时的链接位置
//trans是增加一个字符之后到的状态
//一个状态只有有好多串，但是转移边上只有一个字符
// 一个边上多个字符是后缀树
//其实SAM上的边表示状态转移
//由于状态之间相同的合并了，所以空间较优
#include<bits/stdc++.h>
#define MAXN 3100000
using namespace std;
string s;
int cnt[MAXN],tr[MAXN][30],len[MAXN],fa[MAXN],sz[MAXN];
int last=1,tot=1;
int ans=0;
vector<int>road[MAXN];
void add(int c)
{
     int p=last; //上一次增量的新点的位置
     int now;
     now=last=++tot; //更新新建节点位置
     cnt[now]=1;
     len[now]=len[p]+1; //当前节点的maxlen,如果不分裂，那么maxlen必然是上一个长度+1
     for(;p&&!tr[p][c];p=fa[p]) tr[p][c]=now;
     //更新trans,如果没有这个状态，那么就变成当前状态
     if(!p) fa[now]=1; //fa用来跳link
     //Link向前跳，串越来越小，状态越来越多
     //如果!p 证明这个串的所有后缀(新后缀)的(endpos)一样那么link直接指到1
     else
     {
            //开始拆点
           int q=tr[p][c];
           //这时候有一个转移状态
           //相当于原来有ababc的转移，那么abab加c已经有转移状态
           if(len[q]==len[p]+1) fa[now]=q;
           //如果发现这个点正好是last+1的maxlen，那么就相当于
           //有了一个转移的点，那么直接把now的Link指过去即可
           else
           {
                  //大力拆点
               int spilt=++tot;
               for(int i=0;i<=25;i++)
               {
                      //要拆点，拆成一个maxlen大的x和一个小的y
                   //由于越小放前面
                   //那么小的先和原来的相连，进行信息复制
                   //显然的，一个状态加一个字符都到一个新状态
                   tr[spilt][i]=tr[q][i];
               }
               fa[spilt]=fa[q];
               //spilt是小的，继承状态
               len[spilt]=len[p]+1;
               //发现现在其实只需要改Link
               //trans的作用是转移存在就不用管了
               //由于这个时候多了一个位置
               //那么从断点的位置Link必定改变
               //那么更改Link就可以了
               //发现其实尽管有这个转移边，但是状态不一样
               //那么就可以两个都连想spilt
               fa[q]=fa[now]=spilt;
               for(;p&&tr[p][c]==q;p=fa[p]) tr[p][c]=spilt;
               //更改前面的转移边
           }
     }
}
void dfs(int x)
{
     for(int i=0;i<road[x].size();i++)
     {
          int y=road[x][i];
          dfs(y);
          cnt[x]+=cnt[y];
     }
     if(cnt[x]!=1) ans=max(ans,cnt[x]*len[x]);
//     cout<<cnt[x]*len[x]<<endl;
}
int main()
{
    cin>>s;
    int len=s.size();
    s=' '+s;
    for(int i=1;i<=len;i++)
    {
        add(s[i]-'a');
    }
    for(int i=2;i<=tot;i++)
    {
        road[fa[i]].push_back(i);
        //后缀树
    }
    dfs(1);
    cout<<ans;
}

看一下$add$函数

其余的都是$O(1),$除了几个循环,那么看这几个循环

第一个循环

for(;p&&!tr[p][c];p=fa[p]) tr[p][c]=now;

每个点都有一个$trans$,每个点最多被赋值一次,均摊下来,每个点只被操作一次,点数是状态数,$O(|S|)$

其实你更改的是连续的一部分,每次都会改连续的一段,绝对不会出现一段被多次经过情况,那么每个点至多被经过一次

第二个循环

for(int i=0;i<=25;i++)
{
//要拆点，拆成一个maxlen大的x和一个小的y
//由于越小放前面
//那么小的先和原来的相连，进行信息复制
//显然的，一个状态加一个字符都到一个新状态
tr[spilt][i]=tr[q][i];
}

每次至多多一个状态去复制,那么复杂度是$O(25|S|)$,尽管是个$25$的常数...

第三个循环

for(;p&&tr[p][c]==q;p=fa[p]) tr[p][c]=spilt;
//更改前面的转移边

这个貌似好麻烦...

首先这个东西是更一下转移边,现在不是分成两部分了吗,一个是没有变化的部分,一个是变化的部分

那么改变$tran$的是能到这个旧的状态的需要把这些转移搞到旧状态上(新开的$split$点)来,相当于复制一遍

明确一点,我们第三个循环里的运行条件是tran[p][c]==q,可以发现每次循环的q必然不一样,因为我们会将此节点分裂,那么下一次找到的肯定是endpos小的节点,那么这个第三个循环的复杂度就和tran的个数有关,tran有多少个,总共就会循环多少个

我们改变的是所有与旧状态相连的边,那么我们考虑接下来的所有这个操作,本质是把这个点裂开,那 么考虑下面的裂开操作,是因为这个点的$endpos$变化,又证明,越短的串越容易改变,那么考虑变化的肯定不是这个点,而是这次分裂操作得到的另外一个点,感性理解一下,每次只裂开一个点,总不能把容易变得放一边,把不容易变得裂开吧,也就是说,每个节点至多被遍历到一次,每个节点的连边最多被遍历到一次,那么复杂度就和边数有关了

边数也就是$tran$的数量,在整个$SAM$的数目是$O(|S|)$的(怎么我看到的证明都不是人话啊...)

还是考虑搞一个生成树,目前的$SAM$并不完整

$trans$的作用是能遍历到所有子串,从终止节点往回跑所有以它为结尾的子串(倒着跑),发现不能表示出来了就加边,而且考虑加边的话是因为$endpos$不一样(一样的话就是能顺着跑下来了),那么最多加$endpos$集合大小条边

那么对于每个终止节点都跑一遍,最多加了$\sum(|endpos|)$(就是$endpos$集合大小的和),增加了$O(n)$个

那么$trans$也是$O(n)$了

从$3.7,21:00$开始写,中间有一场模拟赛,直到$3.8,13:05$写完

对着一个证明卡了半天~，像个zz,hhh