CF1656E Equal Tree Sums 题解

题目链接

思路分析

自认为是一道很好的构造题，但是我并不会做。

看了题解后有一些理解，在这里再梳理一遍巧妙的思路。

我们先来看这样的一张图：



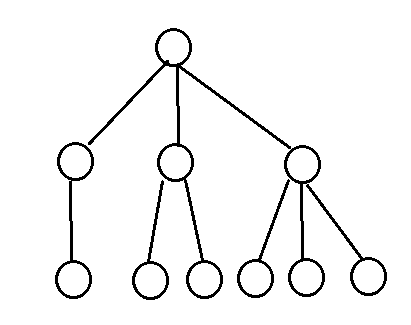
我们发现当去掉叶子节点的父亲时，剩下树的价值和等于叶子节点的价值和，显然全是正的不太可能。

对于叶子节点我们不妨设他们的权值都是 \(1\) ，此时若删去最大的祖先节点，可以发现第二层节点的权值差正好和其儿子的个数差相同。

于是我们初步推断出权值大小可能和儿子的个数有着密切的关系。（实际就是这样）

上面的问题好像没有什么突破口了，我们转而考虑如何确定一个节点的正负问题。

考虑到删掉一个节点后每个子树权值大小相等。猜测出每个节点的权值的正负是交错进行的。

直接用官方题解的话说：

黑白染色，黑点为正，白点为负，绝对值等于当前节点的度数。

这还是很好理解的，就上图而言，当删掉一个节点后，它的权值分配给它所有的子树。

所以每个块的的权值和为 \(1\) 或 \(-1\) 。

Code

代码的话直接模拟即可。

#include <bits/stdc++.h>

#define file(a) freopen(a".in", "r", stdin), freopen(a".out", "w", stdout)

#define Enter putchar('\n')
#define quad putchar(' ')

namespace IO {
template <class T> inline void read(T &a);
template <class T, class ...rest> inline void read(T &a, rest &...x);
template <class T> inline void write(T x);
template <class T, class ...rest> inline void write(T x, rest ...a);
}

#define N 100005

int T, n, x, y, in[N], ans[N];
std::vector <int> dis[N];

inline void dfs(int now, int father, int flag) {
  ans[now] = in[now] * flag;
  for (int t : dis[now]) {
    if (t == father) continue;
    dfs(t, now, -flag);
  }
}

signed main(void) {
  IO::read(T);
  while (T--) {
    IO::read(n);
    for (int i = 1; i <= n; i++) dis[i].clear(), in[i] = 0;
    for (int i = 1, x, y; i < n; i++) {
      IO::read(x, y);
      in[x] ++;
      in[y] ++;
      dis[x].push_back(y);
      dis[y].push_back(x);
    }
    dfs(1, 0, 1);
    for (int i = 1; i <= n; i++)
      printf("%d ", ans[i]);
    Enter;
  }
}

namespace IO {
template <class T> inline void read(T &a) {
  T s = 0, t = 1;
  char c = getchar();
  while ((c < '0' || c > '9') && c != '-')
    c = getchar();
  if (c == '-')
    c = getchar(), t = -1;
  while (c >= '0' && c <= '9')
    s = (s << 1) + (s << 3) + (c ^ 48), c = getchar();
  a = s * t;
}
template <class T, class ...rest> inline void read(T &a, rest &...x) {
  read(a); read(x...);
}

template <class T> inline void write(T x) {
  if (x == 0) putchar('0');
  if (x < 0) putchar('-'), x = -x;
  int top = 0, sta[50] = {0};
  while (x)
    sta[++top] = x % 10, x /= 10;
  while (top)
   putchar(sta[top] + '0'), top --;
   return ;
}
template <class T, class ...rest> inline void write(T x, rest ...a) {
  write(x); quad; write(a...);
}
}