python不确定性计算之模糊动态聚类实验

模糊动态聚类实验

本实验所采用的模糊聚类分析方法是基于模糊关系上的模糊聚类法，也称为系统聚类分析法，可分为三步：

第一步：数据标准化，建立模糊矩阵

第二步：建立模糊相似矩阵

第三步：聚类

本程序读取Excel文件，再由程序读入，在数据标准化中采用了最大值规格法，然后通过夹角余弦法或最大最小法构造模糊相似矩阵，然后按lambda截集进行动态聚类，聚类完成后，采用Xie-Beni指标和F统计指标两种方式进行评判，选出最优聚类和lambda的最优取值。

代码如下：

# -*- coding: utf-8 -*-
import numpy as np
import pprint
import xlrd #读取Excel的扩展工具
from copy import deepcopy
import warnings
#矩阵不用科学计数法的显示方式
np.set_printoptions(suppress=True)

def main():
    path = 'data.xlsx'
    # 0.读取数据
    matrix = read_excel(path)
    # 1.数据标准化
    #k = 2

    while( k != 1 and k != 2 and k !=3 ):
        print('请输入标准化方法：\n1.平移-标准差变换\n2.平移-极差变换\n3.最大值规格法')
        k = eval(input())    

    x_matrix = std_matrix(matrix,k)
    print(x_matrix)
    # 2.构造模糊相似矩阵
    k = -1
    while( k != 1 and k != 2 ):
        print('请输入构造模糊相似矩阵方法：\n1.夹角余弦法\n2.最大最小法')
        k = eval(input())
    if( k == 1 ):
        r_matrix = get_rmatrix1(x_matrix)
    else:
        r_matrix = get_rmatrix2(x_matrix)
    #print('===============标准化特征指标矩阵=============',x_matrix)
    #print('==================模糊相似矩阵R================',r_matrix)
    # 3.求传递闭包t(R)
    i = 0
    while True:
        t_r_matrix = get_tR(r_matrix)
        if (t_r_matrix == r_matrix).all():#每个元素都相等
            break
        else:
            r_matrix = t_r_matrix
            i = i + 1
    # 4.按lambda截集进行动态聚类
    result = lambda_clustering(t_r_matrix)
    warnings.filterwarnings("ignore")#因为存在除0情况，需忽略警告

    # 5.利用Xie_beni指数或F统计寻找最优分类
    k = -1
    while( k != 1 and k != 2 ):
        print('请输入评判Lambda取值的标准：\n1.Xie-Beni指标\n2.F统计指标')
        k = eval(input())
    if( k == 1 ):
        Xie_Beni(result,x_matrix)
    else:
        F_Statistics(result,x_matrix)

# 1.标准化:
def std_matrix(x_matrix,k):
    x = deepcopy(x_matrix)
    #获得特征指标矩阵x的行列数
    x_rows = x.shape[0]#读取矩阵第一维度的长度，即行数
    x_cols = x.shape[1]#读取矩阵第二维度的长度，即列数
    x_mean = np.mean(x,axis = 0)#均值
    x_std = np.std(x,axis = 0)#标准差
    #numerical python
    for i in range(x_rows):
        for j in range(x_cols):
            if(k == 1):
                x[i][j] = (x[i][j] - x_mean[j])/x_std[j]#平移-标准差变换(消除量纲)
            elif(k == 2):
                x[i][j] = ( x[i][j] - min(x[i]) ) / ( max(x[i]) - min(x[i]) )#平移-极差变换
            else:
                x[i][j] = round(x[i][j] / max(x_matrix.T[j]),2)#标准化:最大值规格法
    return x

# 2.构造模糊相似矩阵：采用夹角余弦法
def get_rmatrix1(x_matrix):
    x_rows = x_matrix.shape[0]#读取矩阵第一维度的长度，即行数
    x_cols = x_matrix.shape[1]#读取矩阵第二维度的长度，即列数
    # norm_matrix :每一行的2-范式值
    norm_matrix = np.linalg.norm(x_matrix,axis = 1)
    # r_matrix : 模糊相似矩阵
    r_matrix = np.zeros((x_rows,x_rows),dtype = 'float')#初值为零矩阵
    # 获得模糊相似接矩阵行列数
    r_rows = r_matrix.shape[0]
    r_cols = r_matrix.shape[1]
    for i in range(r_rows):
        for j in range(r_cols):
            #multi_matrix = x_matrix[i] * x_matrix[j]
            r_matrix[i][j] = abs(np.dot(x_matrix[i],x_matrix[j])) / (norm_matrix[i] * norm_matrix[j])#矩阵相乘，再除以2范式之积
    return r_matrix

# 2.构造模糊相似矩阵：采用最大最小法
def get_rmatrix2(x_matrix):
    # r_matrix : 模糊相似矩阵
    r_matrix = np.zeros((x_matrix.shape[0],x_matrix.shape[0]),dtype = 'float')
    for i in range(0,x_matrix.shape[0]):
        for j in range(0,x_matrix.shape[0]):
            max_sum = 0
            min_sum = 0
            for k in range(x_matrix.shape[1]):
                max_sum = max_sum + max(x_matrix[i][k], x_matrix[j][k])
                min_sum = min_sum + min(x_matrix[i][k], x_matrix[j][k])
            r_matrix[i][j] = round(min_sum / max_sum , 2)#最小值之和除以最大值之和
    return r_matrix

# 3.平方法求传递闭包t(R)
def get_tR(r_matrix):
    rows = r_matrix.shape[0]#读取矩阵第一维度的长度，即行数
    cols = r_matrix.shape[1]#读取矩阵第二维度的长度，即列数
    min_list = []
    new_mat = np.zeros((rows,cols),dtype = 'float')
    for m in range(rows):
        for n in range(cols):
            min_list = []
            now_row = r_matrix[m]
            for k in range(len(now_row)):
                #先取小,再取大
                min_cell = min(r_matrix[m][k],r_matrix[:,n][k])#先取小
                min_list.append(min_cell)
            new_mat[m][n] = max(min_list)#再取大
    return new_mat

def lambda_clustering(final_matrix):
    rows = final_matrix.shape[0]#读取矩阵第一维度的长度，即行数
    cols = final_matrix.shape[1]#读取矩阵第二维度的长度，即列数
    result = [] #返回的结果
    global lambda_list
    lambda_list = []  #所有的lambda值
    temp_matrix = np.zeros((rows,cols),dtype = 'float')
    global temp_class_all
    temp_class_all = []

    for i in range(0,rows):
        for j in range(0,cols):
            lambda_list.append(final_matrix[i][j])#提取各个特征值到lambda_list

    #print(final_matrix)
    lambda_list = list(set(lambda_list))#去重
    lambda_list.sort()

    #通过循环，逐个计算lambda值的分类情况
    for i in range(len(lambda_list)):
        temp_matrix = np.zeros((rows,cols),dtype = 'float')
        class_list = []  #分类情况
        mark_list = [] #存储当前lambda值已经被分组的样本
        for m in range(rows):
            for n in range(cols):
                if final_matrix[m][n] >= lambda_list[i]:
                    temp_matrix[m][n] = 1 #大于lambda则赋值为1
        #对某个lambda值进行分类
        for m in range(rows):
            if (m+1) in mark_list:
                continue
            now_class = [] #当前分类情况
            now_class.append(m+1)
            mark_list.append(m+1)
            for n in range(m+1,rows):
                if (temp_matrix[m] == temp_matrix[n]).all() :
                    #进行分类
                    now_class.append(n+1)#每个小的分类表
                    #print(now_class)
                    mark_list.append(n+1) #存储当前lambda值，已经被分组的样本
            class_list.append(now_class) #分类完成
        global temp_class
        temp_class = class_list
        result.append(['matrix:',temp_matrix,'lambda:',lambda_list[i],'class',temp_class])
        temp_class_all.append(temp_class)
    return result

# 5.利用Xie_beni指标寻找最优分类
def Xie_Beni(final_matrix,x_matrix):
    class_num = 0    #当前总类数
    class_list = []  #当前分类情况
    rate = float('inf') #Xie_Beni指数
    flag = 0 #标记Xie_Beni指数最大的分类情况
    i = 0
    for temp in final_matrix:
        this_in_measure = 0    #当前分类的类内紧密度，类中各点与类中心的距离平方和
        this_out_measure = float('inf')   #当前分类的类间分离度，最小的类与类中心的平方
        class_list = temp_class_all[i]
        class_num = len(class_list)
        means_list = [np.zeros((1,x_matrix.shape[1]),dtype = 'float')]*class_num #该分类下，每一类的均值
        #遍历每一类
        for i in range(class_num):
            #求每一类的类中心
            this_class_num = len(class_list[i])
            this_sum = np.zeros((1,x_matrix.shape[1]),dtype = 'float')
            this_means = np.zeros((1,x_matrix.shape[1]),dtype = 'float')
            for j in range(this_class_num):
                this_sum += x_matrix[class_list[i][j]-1]
            this_means = this_sum / this_class_num
            means_list[i] = this_means

        #计算当前分类类间分离度
        for m in range(len(means_list)):
            if len(means_list) == 1:
                this_out_measure = 0 #当所有样本分为一类的时候，类间分离度为无穷大，但这样的分类没有任何意义，所以置0，不予以比较。
                break
            for n in range(m+1,len(means_list)):
                temp = np.linalg.norm(means_list[m] - means_list[n])#计算向量欧氏距离
                if temp < this_out_measure:
                    this_out_measure = temp

        #计算当前分类类内紧密度
        for m in range(class_num):
            this_class_num = len(class_list[i])
            for n in range(this_class_num):
                add = np.linalg.norm(means_list[m] - np.array([x_matrix[n-1]]))#计算向量欧氏距离
                this_in_measure = this_in_measure + add

        this_rate = this_in_measure /  this_out_measure# 类内距离 ÷ 类间距离

        print('lambda =',round(lambda_list[i],2))
        print("Xie_Beni指数为%.2f"%this_rate)
        print('当前分类为',class_list)
        print("================================================")
        if (this_rate < rate):
            rate = this_rate
            flag = class_list
            best_lambda = lambda_list[i]
            min_num = this_rate
        i = i + 1

    print("****************最优分类结果如下****************")
    print('lambda的最优取值为 %.2f'%best_lambda)
    print('Xie_Beni指数最小值为%.2f'%min_num)
    print('最优分类为',flag)

# 5.利用 F统计指标
def F_Statistics(results, standard_matrix):
    #定义变量F 为F统计量数值    #定义class_class变量为类与类之间的距离  F的分子#    定义class_sample变量为类内样品间的距离  F的分母
    temp_F = []
    k = 0
    #print('temp_class_all:',temp_class_all)
    for result in results:
        mean_all = np.mean(standard_matrix, axis=0)#计算矩阵所有样品属性的平均值
        sorts = temp_class_all
        class_class = 0
        class_sample = 0

        #对于每个分类
        for sort in sorts:
            sort = sort[0]
            sort = [i-1 for i in sort]#将分类转化 [4, 9, 10]-->[3, 8, 9]因为矩阵下标从零开始
            # print(standard_matrix[sort])
            mean_j = np.mean(standard_matrix[sort], axis=0)#计算矩阵第j类样品的平均值

            #类间距离
            xj_av_reduce_xall_av = (np.sum((np.square(mean_j - mean_all)), axis=0))**(1/2) #第j类样品的平均值 - 所有样品属性的平均值
            class_class = class_class + (len(sort) * xj_av_reduce_xall_av**2)

            #计算类class_sample 为类内样品间的距离
            sum_xij_reduce_xj_av = 0#用来储存这个类中所有样品的xij_reduce_xj_av值
            for s in sort:#求每一个样品的xij_reduce_xj_av，对所有属性
                xij_reduce_xj_av = (np.sum(np.square((standard_matrix[s] - mean_j)), axis=0))**(1/2) #计算x(i,j) - 第j类样品的平均值
                sum_xij_reduce_xj_av = sum_xij_reduce_xj_av + (xij_reduce_xj_av**2)
            class_sample = class_sample + sum_xij_reduce_xj_av #类内样品间的距离

        F = (class_class / (len(sorts[k])-1)) / (class_sample / (standard_matrix.shape[0] - len(sorts[k]))) #类间距离 ÷ 类内距离

        if(F == float('inf')):
            #当所有样本分为一类的时候，类间分离度为无穷大，但这样的分类没有任何意义，所以置0，不予以比较。
            F = 0
        F = round(F,2)
        temp_F.append(F)

        print('lambda =',round(lambda_list[k],2))
        print('F统计量为',F)
        print('当前分类结果',temp_class_all[k])
        print("================================================")
        k = k + 1

    print("****************最优分类结果如下****************")
    print('lambda的最优取值为 %.2f'%lambda_list[np.argmax(temp_F)])
    print('F统计量最大值为%.2f'%max(temp_F))
    print('最优分类为',temp_class_all[np.argmax(temp_F)])#取F最大时候的下标

# 7.读取excel目录
def read_excel(path):
    #打开exel
    workbook = xlrd.open_workbook(path,'r')
    #获得sheet1名字
    sheet1 = workbook.sheets()[0]
    rows = sheet1.nrows
    cols = sheet1.ncols
    #建立特征指标矩阵
    x_matrix = np.zeros((rows-1,cols-1),dtype = 'float')
    #第一行是列名，从第二行开始
    for i in range(0,rows-1):
        #第一列是序号，从第二列开始
        for j in range(0,cols-1):
            x_matrix[i][j]= sheet1.cell(i+1,j+1).value
    return x_matrix

if __name__ == '__main__':
    main()

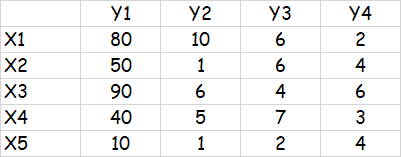
测试表格如下：