基于python的数学建模---洛伦兹线与数值解

import numpy as np
from scipy.integrate import odeint
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt

def dmove(Point, t, sets):
    p, r, b = sets
    x, y, z = Point
    return np.array([p * (y - x), x * (r - z), x * y - b * z])

t = np.arange(0, 30, 0.001)
#             func   y0         时间       超参  赋值给 P,R,B的值
P1 = odeint(dmove, (0., 1., 0.), t, args=([10., 28., 3.],))
#odeint 是将时间下所对应的x,y,z值求出
P2 = odeint(dmove, (0., 1.01, 0.), t, args=([10., 28., 3.],))
fig = plt.figure()
ax = Axes3D(fig)
#         X        Y         Z
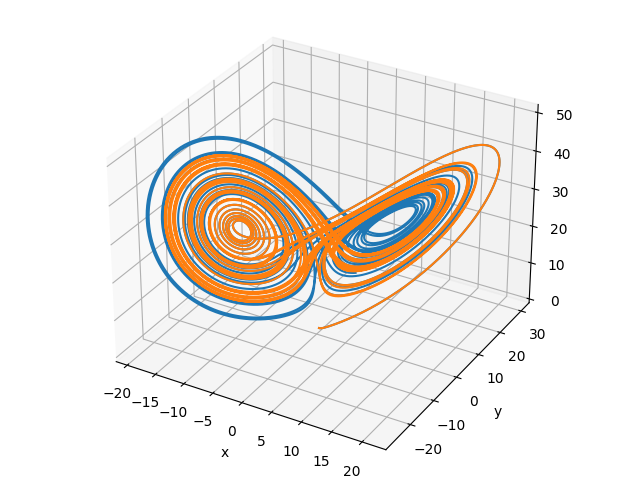
ax.plot(P1[:, 0], P1[:, 1], P1[:, 2])
ax.plot(P2[:, 0], P2[:, 1], P2[:, 2])
plt.xlabel("x")
plt.ylabel("y")
plt.show()