【二分答案+贪心】UVa 1335 - Beijing Guards

Beijing was once surrounded by four rings of city walls: the Forbidden City Wall, the Imperial City Wall, the Inner City Wall, and finally the Outer City Wall. Most of these walls were demolished in the 50s and 60s to make way for roads. The walls were protected by guard towers, and there was a guard living in each tower. The wall can be considered to be a large ring, where every guard tower has exaetly two neighbors.

The guard had to keep an eye on his section of the wall all day, so he had to stay in the tower. This is a very boring job, thus it is important to keep the guards motivated. The best way to motivate a guard is to give him lots of awards. There are several different types of awards that can be given: the Distinguished Service Award, the Nicest Uniform Award, the Master Guard Award, the Superior Eyesight Award, etc. The Central Department of City Guards determined how many awards have to be given to each of the guards. An award can be given to more than one guard. However, you have to pay attention to one thing: you should not give the same award to two neighbors, since a guard cannot be proud of his award if his neighbor already has this award. The task is to write a program that determines how many different types of awards are required to keep all the guards motivated.

Input

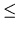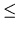The input contains several blocks of test eases. Each case begins with a line containing a single integer ln100000, the number of guard towers. The next n lines correspond to the n guards: each line contains an integer, the number of awards the guard requires. Each guard requires at least 1, and at most l00000 awards. Guard i and i + 1 are neighbors, they cannot receive the same award. The first guard and the last guard are also neighbors.

The input is terminated by a block with n = 0.

Output

For each test case, you have to output a line containing a single integer, the minimum number x of award types that allows us to motivate the guards. That is, if we have x types of awards, then we can give as many awards to each guard as he requires, and we can do it in such a way that the same type of award is not given to neighboring guards. A guard can receive only one award from each type.

Sample Input

3
4
2
2
5
2
2
2
2
2
5
1
1
1
1
1
0

Sample Output

8
5
3

题意: 有n个人, 每人都需要wi种礼物, 但是相邻的人得礼物是不可以相同的, 现在要你求出最少的礼物数满足全部人的需求, 每种礼物的数量是无限的.

解题思路:

1. 当n为偶数时, 答案是相邻两人之间的的w值最大和, 即p = max{ p, wi + wi+1 }.并且可以看出，此p为礼物数的下限。

2. 当n为奇数时, 采用二分答案求解, 左边界为相邻两人之间wi值最大和（注意奇数情况时，第1人和第n人会导致冲突），右边界为所有人的wi值之和；假设p种礼物是否满足分配:

假设: 第一个人得到礼物1~r1, 分配的贪心策略可以是: 偶数编号的人尽量往前取, 奇数的人尽量往后取. 这样需要第n个人在不冲突的条件下, 尽量可能的往后取wn样礼物. 最后判断编号1和编号n的人是否冲突即可.

例: p = 8, r = {2,2,5,2,5}

第一人:{1,2}, 第二人:{3,4}, 第三人:{8,7,6,5,2}, 第四人:{1,3}, 第五人:{8,7,6,5,4}

 bool ok(int m)
 {
     Left[] = w[]; Right[] = ;
     for(int i = ; i < n; i++)
     {
         if(i%)
         {
             if(w[]-Left[i-]-w[i] >= )
             {
                 Left[i] = w[i];
                 Right[i] = ;
             }
             else
             {
                 Left[i] = w[]-Left[i-];
                 Right[i] = w[i]-Left[i];
             }
         }
         else
         {
             if(m-w[]-Right[i-]-w[i] >= )
             {
                 Left[i] = ;
                 Right[i] = w[i];
             }
             else
             {
                 Right[i] = m-w[]-Right[i-];
                 Left[i] = w[i]-Right[i];
             }
         }
     }
     return Left[n-] == ;
 }

如家大神的比自己的简单诶。自己以后得学会简化算法：

bool ok(int m)
{
    Left[] = w[]; Right[] = ;
    for(int i = ; i < n; i++)
    {
        if(i%)
        {
            Left[i] = min(w[]-Left[i-], w[i]);
            Right[i] = w[i] - Left[i];
        }
        else
        {
            Right[i] = min(m-w[]-Right[i-], w[i]);
            Left[i] = w[i]-Right[i];
        }
    }
    return Left[n-] == ;
}

附代码：

 #include<iostream>
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>

 using namespace std;
 const int maxn = ;
 int n, ans;
 int w[maxn];
 int Left[maxn], Right[maxn];

 bool ok(int m)
 {
     Left[] = w[]; Right[] = ;
     for(int i = ; i < n; i++)
     {
         if(i%)
         {
             Left[i] = min(w[]-Left[i-], w[i]);
             Right[i] = w[i] - Left[i];
         }
         else
         {
             Right[i] = min(m-w[]-Right[i-], w[i]);
             Left[i] = w[i]-Right[i];
         }
     }
     return Left[n-] == ;
 }

 int main()
 {
     while(scanf("%d", &n) && n)
     {
         ans = ;
         for(int i = ; i < n; i++)
             scanf("%d", &w[i]);
         if(n == ) {printf("%d\n", w[]); continue;}
         w[n] = w[];
         int L = , R = ;
         for(int i = ; i < n; i++)
         {
             L = max(L, w[i]+w[i+]);
             R += w[i];
         }
         if(n%)
         {
             while(L < R)
             {
                 int M = L + (R-L)/;
                 if(ok(M)) R = M;
                 else L = M+;
             }
         }
         printf("%d\n", L);
     }
     return ;
 }