HDU 5430：Reflect 欧拉函数

Reflect

 Accepts: 72

 Submissions: 302

 Time Limit: 2000/1000 MS (Java/Others)

 Memory Limit: 65536/65536 K (Java/Others)

问题描述

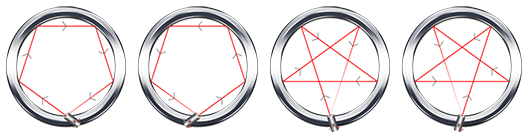
从镜面材质的圆上一点发出一道光线反射NN次后首次回到起点。
问本质不同的发射的方案数。

输入描述

第一行一个整数T，表示数据组数。T \leq 10T≤10
对于每一个组，共一行，包含一个整数，表示正整数N(1 \leq N \leq 10^{6})N(1≤N≤10​6​​)。

输出描述

对于每一个组，输出共一行，包含一个整数，表示答案。

输入样例

1
4

输出样例

4

如果k/(N+1)不是既约分数的话，即可以约分，说明该方案之前出现过，这次只不过所有的线跑了两遍，不符合题目中“首次”回到起点的含义。所以就是求有多少个k符合条件。

代码：

#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
#include <string>
#include <cstring>
#pragma warning(disable:4996)
using namespace std;

int euler(int n)
{
	int res = n, a = n;
	for (int i = 2; i*i <= a; i++)
	{
		if (a%i == 0)
		{
			res = res / i*(i - 1);
			while (a%i == 0)a /= i;
		}
	}
	if (a > 1)res = res / a*(a - 1);
	return res;
}

int main()
{
	int test;
	cin >> test;
	int n;
	while (test--)
	{
		cin >> n;
		cout << euler(n+1) << endl;
	}

	return 0;
}

版权声明：本文为博主原创文章，未经博主允许不得转载。