JavaScript图形实例:迭代函数系统生成图形
迭代函数系统(Iterated Function System,IFS)可以用来创建分形图案,它是分形理论的重要分支,也是分形图形处理中最富生命力而且最具有广阔应用前景的领域之一。这一工作最早可以追溯到Hutchinson于1981年对自相似集的研究。美国科学家M.F.Barnsley于1985年发展了这一分形构型系统,并命名为迭代函数系统(Iterated Function System,IFS),后来又由Stephen Demko等人将其公式化,并引入到图像合成领域中。IFS将待生成的图像看做是由许多与整体相似的(自相似)或经过一定变换与整体相似的(自仿射)小块拼贴而成。
IFS算法的基本过程是:
(1)设定一个起始点(x0,y0)及总的迭代步数。
(2)以概率P选取仿射变换W,形式为
x1=a*x0 + b*y0 + e
y1=c*x0 + d*y0 + f
(3)以W作用点(x0,y0),得到新坐标(x1,y1);
(4)在屏幕上坐标(x1,y1)处描点;
(5)令x0=x1,y0=y1,为下一次迭代做准备;
(6)返第(2)步,进行下一次迭代,直到迭代次数大于总步数为止。
例如,在一个二维平面中,有2种仿射变换函数,可以将一个点映射到另一个位置:
① x(n+1)= 0.5*x(n)-0.5*y(n)
y(n+1) = 0.5*x(n)+0.5* y(n)
② x(n+1) = 0.5 * x(n)+0.5 * y(n)+0.5
y(n+1) = -0.5 * x(n) + 0.5 * y(n) + 0.5
给定一个初始点 x(0),y(0),经过上面的仿射变换函数的映射,便可以得到平面中许多点,这些点构成的图形便是分形图案。这个系统就叫做迭代函数系统。
但是,一共有2个仿射变换函数,每次迭代要使用哪一个呢?因此,需要给每个仿射变换函数规定一个概率,按照概率来进行选择。
不妨设2个仿射变换函数的概率均为0.5(各一半),此时算法步骤为:
(1)生成一个0~1之间的随机数r;
(2)判断随机数落入哪一个概率空间,若r<=0.5,则使用仿射变换函数①;否则使用仿射变换函数②;
(3)根据仿射变换函数计算出新坐标(x1,y1),并在该坐标处画一个点;
(4)循环执行这一过程,直到达到规定次数。
按上面的算法步骤,编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>IFS生成图形(一)</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var ctx=canvas.getContext('2d');
ctx.fillStyle="#EEEEFF";
ctx.fillRect(0,0,600,600);
ctx.fillStyle="red";
var x0=0;
var y0=0;
for (i=0; i<100000; i++)
{
r=Math.random();
if (r<=0.5)
{
x1=0.5*x0-0.5*y0;
y1=0.5*x0+0.5*y0;
}
else
{
x1=0.5*x0+0.5*y0+0.5;
y1=-0.5*x0+0.5*y0+0.5;
}
ctx.fillText('.',x1*200+200,y1*200+200);
x0 = x1;
y0 = y1;
}
}
</script>
</head>
<body onload="draw('myCanvas');">
<canvas id="myCanvas" width="600" height="600" style="border:3px double #996633;">
</canvas>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出的C曲线,如图1所示。

图1 利用IFS方法生成的C曲线
如果将上面的映射函数改为:
① x(n+1)= -0.82*x(n)+0.16*y(n)+137
y(n+1) = -0.16*x(n)+0.81* y(n)+14
② x(n+1) = 0.44 * x(n)+0.32 * y(n)-3
y(n+1) = -0.07 * x(n) + 0.61 * y(n) + 70
对应的HTML文件如下:
<!DOCTYPE html>
<head>
<title>IFS生成图形(一)</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var ctx=canvas.getContext('2d');
ctx.fillStyle="#EEEEFF";
ctx.fillRect(0,0,600,600);
ctx.fillStyle="green";
var x0=0;
var y0=0;
for (i=0; i<100000; i++)
{
r=Math.random();
if (r<=0.5)
{
x1=-0.82*x0+0.16*y0+137;
y1=-0.16*x0+0.81*y0+14;
}
else
{
x1=0.44*x0+0.32*y0-3;
y1=-0.07*x0+0.61*y0+70;
}
ctx.fillText('.',x1*2+100,y1*2+100);
x0 = x1;
y0 = y1;
}
}
</script>
</head>
<body onload="draw('myCanvas');">
<canvas id="myCanvas" width="600" height="600" style="border:3px double #996633;">
</canvas>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出如图2所示的树叶图案。

图2 利用IFS生成的树叶
由图1和图2的生成程序可知,IFS方法中仿射变换的形式是相同的,不同的形状取决于仿射变换的系数(a,b,c,d,e,f),并且对于一个比较复杂的图形,可能需要多个不同的仿射变换来实现,并且每一个仿射变换函数被调用的概率P也不一定是等同的。因此,6个仿射变换系数(a,b,c,d,e,f)和一个概率p便构成了IFS算法最关键的部分——IFS码。
1.SierPinski三角形
SierPinski三角形采用的仿射变换函数为:
W1: x1=0.5*x0
y1=0.5*y0
W2: x1=0.5*x0 + 0.5
y1=0.5*y0
W3: x1=0.5*x0 +0.25
y1= 0.5*y0 +0.5
可以让3个仿射变换函数的调用概率相同或相近,即概率p分别取0.333,0.333,0.334,保证p1+p2+p3=1。
为程序设计简洁,将IFS码中的6个系数和概率p采用数组保存。编写如下的HTML代码(为了后面叙述方便,将这段程序代码记为“IFS生成图形(二)”)。
<!DOCTYPE html>
<head>
<title>IFS生成图形(二)</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var ctx=canvas.getContext('2d');
ctx.fillStyle="#EEEEFF";
ctx.fillRect(0,0,500,500);
ctx.fillStyle="red";
var a=[0.5,0.5,0.5];
var b=[0,0,0];
var c=[0,0,0];
var d=[0.5,0.5,0.5];
var e=[0,0.5,0.25];
var f=[0,0,0.5];
var p=[0.333,0.333,0.334];
var x0=0;
var y0=0;
for (i=0; i<10000; i++)
{
r=Math.random();
if (r<=p[0])
index=0;
else if (r<=p[0]+p[1])
index=1;
else
index=2;
x1=a[index]*x0+b[index]*y0+e[index];
y1=c[index]*x0+d[index]*y0+f[index];
ctx.fillText('.',x1*300+100,400-y1*300);
x0 = x1;
y0 = y1;
}
}
</script>
</head>
<body onload="draw('myCanvas');">
<canvas id="myCanvas" width="500" height="500" style="border:3px double #996633;">
</canvas>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出的SierPinski三角形,如图3所示。

图3 SierPinski三角形
前面介绍过,IFS的关键部分是IFS码,不同的IFS码生成不同的图形。
例如,“IFS生成图形(二)”程序中的IFS码定义改写为:
var a=[0.5,0.5,0.5];
var b=[0,0,0];
var c=[0,0,0];
var d=[0.5,0.5,0.5];
var e=[0,0.5,0.5];
var f=[0,0.5,0];
var p=[0.333,0.333,0.334];
则在浏览器窗口中绘制出如图4所示的直角SierPinski三角形。

图4 直角SierPinski三角形
2.蕨类植物
可以使用4个仿射变换函数来生成蕨类植物的图案,编写如下的HTML代码(为了后面叙述方便,将这段程序代码记为“IFS生成图形(三)”)。
<!DOCTYPE html>
<head>
<title>IFS生成图形(三)</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var ctx=canvas.getContext('2d');
ctx.fillStyle="#EEEEFF";
ctx.fillRect(0,0,600,600);
ctx.fillStyle="green";
var a=[0,0.2,-0.15,0.85];
var b=[0,-0.26,0.28,0.04];
var c=[0,0.23,0.26,-0.04];
var d=[0.16,0.22,0.24,0.85];
var e=[0,0,0,0];
var f=[0,1.6,0.44,1.6];
var p=[0.01,0.07,0.07,0.85];
var x0=0;
var y0=0;
for (i=0; i<100000; i++)
{
r=Math.random();
if (r<=p[0])
index=0;
else if (r<=p[0]+p[1])
index=1;
else if (r<p[0]+p[1]+p[2])
index=2;
else
index=3;
x1=a[index]*x0+b[index]*y0+e[index];
y1=c[index]*x0+d[index]*y0+f[index];
ctx.fillText('.',x1*50+300,550-y1*50);
x0 = x1;
y0 = y1;
}
}
</script>
</head>
<body onload="draw('myCanvas');">
<canvas id="myCanvas" width="600" height="600" style="border:3px double #996633;">
</canvas>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出的蕨类植物图案,如图5所示。

图5 IFS方法生成的蕨类植物(一)
将“IFS生成图形(三)”程序中的IFS码定义改写为:
var a=[0,0.21,-0.2,0.85];
var b=[0,-0.25,0.26,0.1];
var c=[0,0.25,0.23,-0.05];
var d=[0.16,0.21,0.22,0.85];
var e=[0,0,0,0];
var f=[0,0.44,0,0.6];
var p=[0.01,0.07,0.07,0.85];
可在浏览器窗口中绘制出如图6所示的蕨类植物。

图6 IFS方法生成的蕨类植物(二)
3.树形图案
将“IFS生成图形(二)”程序中的IFS码定义改写为:
var a=[0.387,0.441,-0.468];
var b=[0.430,-0.091,0.020];
var c=[0.430,-0.009,-0.113];
var d=[-0.387,-0.322,0.015];
var e=[0.2560,0.4219,0.4];
var f=[0.5220,0.5059,0.4];
var p=[0.333,0.333,0.334];
可在浏览器窗口中绘制出如图7所示的嫩枝图案。
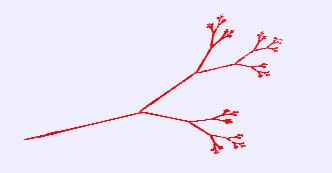
图7 嫩枝
将“IFS生成图形(三)”程序中的IFS码定义改写为:
var a=[0.01,-0.01,0.42,0.42];
var b=[0,0,-0.42,0.42];
var c=[0,0,0.42,-0.42];
var d=[0.45,-0.45,0.42,0.42];
var e=[0,0,0,0];
var f=[0,0.4,0.4,0.4];
var p=[0.05,0.15,0.4,0.4];
可在浏览器窗口中绘制出如图8所示的树形图案。
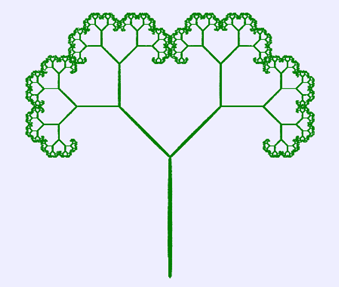
图8 树形图案(一)
将“IFS生成图形(三)”程序中的IFS码定义改写为:
var a=[0,0.42,0.42,0.1];
var b=[0,-0.42,0.42,0];
var c=[0,0.42,-0.42,0];
var d=[0.5,0.42,0.42,0.4];
var e=[0,0,0,0];
var f=[0,0.4,0.4,0.4];
var p=[0.05,0.4,0.4,0.15];
可在浏览器窗口中绘制出如图9所示的树形图案,并好像还有蝉在树上。

图9 树上的蝉
将“IFS生成图形(三)”程序中的IFS码定义改写为:
var a=[0.03,-0.03,0.56,0.56];
var b=[0,0,-0.56,0.56];
var c=[0,0,0.56,-0.56];
var d=[0.45,-0.45,0.56,0.56];
var e=[0,0,0,0];
var f=[0,0.4,0.4,0.4];
var p=[0.05,0.15,0.4,0.4];
可在浏览器窗口中绘制出如图10所示的树形图案。

图10 树形图案(二)
将“IFS生成图形(三)”程序中的IFS码定义改写为:
var a=[-0.04,-0.65,0.41,0.52];
var b=[0,0,0.46,-0.35];
var c=[-0.19,0,-0.39,0.25];
var d=[-0.47,0.36,0.61,0.74];
var e=[-0.12,0.06,0.46,-0.48];
var f=[0.3,1.56,0.4,0.38];
var p=[0.25,0.25,0.25,0.25];
可在浏览器窗口中绘制出如图11所示的树形图案。

图11 树形图案(三)
还可以使用5个仿射变换函数来生成树形图案,参照“IFS生成图形(二)”和“IFS生成图形(三)”,适当添加一个条件选择语句即可,这里不再给出源程序。
5个仿射变换函数的IFS码定义如下:
var a=[0.195,0.462,-0.058,-0.035,-0.637];
var b=[-0.488,0.414,-0.07,0.07,0];
var c=[0.344,-0.252,0.453,-0.469,0];
var d=[0.433,0.361,-0.111,-0.022,0.501];
var e=[0.4431,0.2511,0.5976,0.4884,0.8562];
var f=[0.2452,0.5692,0.0969,0.5069,0.2513];
var p=[0.25,0.25,0.25,0.2,0.05];
可在浏览器窗口中绘制出如图12所示的树形图案。

图12 树形图案(四)
4.雪花
将“IFS生成图形(三)”程序中的IFS码定义改写为:
var a=[0.255,0.255,0.255,0.37];
var b=[0,0,0,-0.642];
var c=[0,0,0,0.642];
var d=[0.255,0.255,0.255,0.37];
var e=[0.3726,0.1146,0.6306,0.6356];
var f=[0.6714,0.2232,0.2232,-0.0061];
var p=[0.2,0.2,0.2,0.4];
可在浏览器窗口中绘制出如图13所示的雪花图案。

图13 雪花图案(一)
还可以使用5个仿射变换函数来生成雪花图案,IFS码定义如下:
var a=[0.382,0.382,0.382,0.382,0.382];
var b=[0,0,0,0,0];
var c=[0,0,0,0,0];
var d=[0.382,0.382,0.382,0.382,0.382];
var e=[0.3072,0.6033,0.0139,0.1253,0.492];
var f=[0.619,0.4044,0.4044,0.0595,0.0595];
var p=[0.2,0.2,0.2,0.2,0.2];
可在浏览器窗口中绘制出如图14所示的雪花图案。

图14 雪花图案(二)
JavaScript图形实例:迭代函数系统生成图形的更多相关文章
- javascript学习笔记--迭代函数
概要 这里的迭代函数指的是对数组对象的操作方法,js数组共有五个迭代函数:every.fifter.forEach.map.some. 1.every every方法,返回值为Boolean类型,tr ...
- JavaScript图形实例:再谈IFS生成图形
在“JavaScript图形实例:迭代函数系统生成图形”一文中,我们介绍了采用迭代函数系统(Iterated Function System,IFS)创建分形图案的一些实例.在该文中,仿射变换函数W的 ...
- JavaScript图形实例:随机SierPinski三角形
在“JavaScript图形实例:SierPinski三角形”中,我们介绍了SierPinski三角形的基本绘制方法,在“JavaScript图形实例:迭代函数系统生成图形”一文中,介绍了采用IFS方 ...
- JavaScript图形实例:线段构图
在“JavaScript图形实例:四瓣花型图案”和“JavaScript图形实例:蝴蝶结图案”中,我们绘制图形时,主要采用的方法是先根据给定的曲线参数方程计算出两点坐标,然后将两点用线段连接起来,线段 ...
- JavaScript的迭代函数与迭代函数的实现
前言 如果对技术很自信,请直接看 实现的源码 如果想回顾一下基础,请按文章顺序阅读 说到迭代方法,最先想到的是什么?forEach还是map,迭代的方法ES5提供了5种方法 以下定义来自 Ja ...
- JavaScript中字符串分割函数split用法实例
这篇文章主要介绍了JavaScript中字符串分割函数split用法,实例分析了javascript中split函数操作字符串的技巧,非常具有实用价值,需要的朋友可以参考下 本文实例讲述了JavaSc ...
- C语言图形界面常用函数集锦
(以下函数均应在图形方式初始之后使用(initgraph(a,b)),在win-tc中使用BGI图形程序模板时,其中已经定义有一个initgr函数,在main函数中应在执行initgr函数之后再使用这 ...
- 混沌分形之迭代函数系统(IFS)
IFS是分形的重要分支.它是分形图像处理中最富生命力而且最具有广阔应用前景的领域之一.这一工作最早可以追溯到Hutchinson于1981年对自相似集的研究.美国科学家M.F.Barnsley于198 ...
- OpenGL学习进程(8)第六课:点、边和图形(三)绘制图形
本节是OpenGL学习的第六个课时,下面介绍OpenGL图形的相关知识: (1)多边形的概念: 多边形是由多条线段首尾相连而形成的闭合区域.OpenGL规定,一个多边形必须是一个“凸多边形”. ...
随机推荐
- Java实现蓝桥杯正则问题
题目描述 考虑一种简单的正则表达式: 只由 x ( ) | 组成的正则表达式. 小明想求出这个正则表达式能接受的最长字符串的长度. 例如 ((xx|xxx)x|(x|xx))xx 能接受的最长字符串是 ...
- java实现第六届蓝桥杯九数分三组
九数分三组 题目描述 1~9的数字可以组成3个3位数,设为:A,B,C, 现在要求满足如下关系: B = 2 * A C = 3 * A 请你写出A的所有可能答案,数字间用空格分开,数字按升序排列. ...
- java代码(6) ---guava之multimap
guava之multimap 上一篇说的是Multiset它可以对存入的相同元素做一个计数的功能,那multimap呢? 一.概述 1.基本介绍和案例说明 multimap和Multiset的继承结果 ...
- 记一次discuz修改首页图片路径问题
1.找到图片路径拼装文件 首先打开根目录下的template目录找到首页文件 打开后找到图片列表的拼装位置 // 链接示例: <!--{eval $imagelistkey = getforum ...
- mysql基础-新版5.7.10源码安装-记录(一)
0x01 MySQL 从 5.5 版本开始,通过 ./configure 进行编译配置方式已经被取消,取而代之的是 cmake 工具 引用一句话 cmake的重要特性之一是其独立于源码(out-of- ...
- zabbix 大流量断图
一. 环境介绍 系统版本:Centos7.4 zabbix-agent 版本:zabbix-agent 3.4.7 二. 问题现象 在使用zabbix的snmp方式的监控端口流量时,某一个图总是断 ...
- 华为EMUI在service中不能打印debug级别的日志
华为emui在service里面不能打印debug级别的日志,因为这个小问题调试了一上午,刚开始我还以为emui把系统service的启动流程都改了呢
- js 不同时间格式介绍以及相互间的转换
首先必须要提到的是 Date 对象,它用来处理时间和日期. 使用 new Date() 语句可创建 Date 对象,创建出来的时间格式如下(后面提到的标准时间都是指该格式): Wed Jul 17 2 ...
- 1.4 Spring 依赖注入(DI)和控制反转(IOC)详解
自己开发了一个股票智能分析软件,功能很强大,需要的点击下面的链接获取: https://www.cnblogs.com/bclshuai/p/11380657.html 1.1 Spring 依赖注 ...
- Python 3中,import win32com.client 出错
在 import win32com.client 时,出现了界面: Traceback (most recent call last): File "<pyshell#1>&qu ...
