【python深度学习】KS,KL,JS散度 衡量两组数据是否同分布

目录

• KS(不需要两组数据相同shape)
• JS散度（需要两组数据同shape）

KS(不需要两组数据相同shape)

• 奇怪之处：有的地方也叫KL
• KS距离，相对熵，KS散度
• 当P(x)和Q(x)的相似度越高，KS散度越小
• KS散度主要有两个性质：
  
  （1）不对称性
  
  不对称性尽管KL散度从直观上是个度量或距离函数，但它并不是一个真正的度量或者距离，因为它不具有对称性，即D(P||Q)!=D(Q||P)
  
  （2）非负性
  
  相对熵的值是非负值，即D(P||Q)>0
  
  

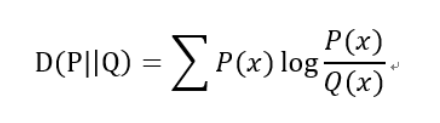
from scipy.stats import ks_2samp
beta=np.random.beta(7,5,1000)
norm=np.random.normal(0,1,1000)
ks_2samp(beta,norm)

• 原假设：beta和norm服从相同的分布。

JS散度（需要两组数据同shape）

JS散度基于KL散度，同样是二者越相似，JS散度越小。

• JS散度的取值范围在0-1之间，完全相同时为0
• JS散度是对称的
  
  

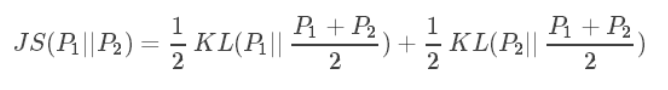
import numpy as np
import scipy.stats
p=np.asarray([0.65,0.25,0.07,0.03])
q=np.array([0.6,0.25,0.1,0.05])
q2=np.array([0.1,0.2,0.3,0.4])
def JS_divergence(p,q):
    M=(p+q)/2
    return 0.5*scipy.stats.entropy(p, M)+0.5*scipy.stats.entropy(q, M)
print(JS_divergence(p,q))  # 0.003093977084273652
print(JS_divergence(p,q2)) # 0.24719159952098618
print(JS_divergence(p,p)) # 0.0