求矩阵最少(或最多)路径和(python实现)
1.递归方式
求最短,最终状态即右下角
f(v, i, j) = min(f(v, i - 1, j), f(v, i, j - 1)) + v[i][j]
最长只需将min改为max即可
import numpy as np
# i:行
# j:列
# v:矩阵
def f(v, i, j):
if i == 0 and j == 0:
return v[0][0]
elif i == 0:
return f(v, i, j - 1) + v[i][j]
elif j == 0:
return f(v, i - 1, j) + v[i][j]
else:
return min(f(v, i - 1, j), f(v, i, j - 1)) + v[i][j]
v = np.array([[1, 3, 5, 9], [8, 1, 3, 4], [5, 0, 6, 1], [8, 8, 4, 0]])
print(f(v, 3, 3))
2.递推方式
注意到只能往右或往下,可以想象,每下一层是右方或下方,而矩阵中,可以想象是以平行与对角线方向为一层,一层层从左上角到右下角递推
即运行一半为如此:
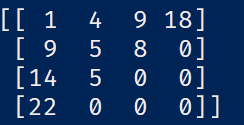
运行完全部为如此

而一层层,每层每一单元取左或上累计最少的数加上本身
即
f[i][j] = min(f[i - 1]f[j], f[i]f[j - 1]) + v[i][j]
因此:代码如下:
import numpy as np
# i:行
# j:列
# v:矩阵
def f(v, n):
s = np.array([[0] * n] * n)
for p in range(n):
for i in range(p + 1):
j = p - i
if i == 0 and j == 0:
s[0][0] = v[0][0]
elif i == 0:
s[0][j] = s[0][j - 1] + v[0][j]
elif j == 0:
s[i][0] = s[i - 1][0] + v[i][0]
else:
s[i][j] = min(s[i - 1][j], s[i][j - 1]) + v[i][j]
limit = 0
for p in range(n, 2 * n - 1):
limit += 1
for i in range(limit, p - limit + 1):
j = p - i
if i == 0 and j == 0:
s[0][0] = v[0][0]
elif i == 0:
s[0][j] = s[0][j - 1] + v[0][j]
elif j == 0:
s[i][0] = s[i - 1][0] + v[i][0]
else:
s[i][j] = min(s[i - 1][j], s[i][j - 1]) + v[i][j]
return s
v = np.array([[1, 3, 5, 9], [8, 1, 3, 4], [5, 0, 6, 1], [8, 8, 4, 0]])
print(f(v, 4))
最后统计出的矩阵的右下即为最少路径和(s[n-1][n-1])
而通过返回s[n-1],我们可以看到路径,从左上角开始,取每一层最小值(不可单独面对方向,可能会陷入陷阱,中途进入错误路径),代码实现如下:
def view(s, n):
string = ''
for p in range(n):
min = 0
for i in range(p + 1):
j = p - i
if min == 0:
min = s[i][j]
elif min > s[i][j]:
min = s[i][j]
string += str(min) + '->'
limit = 0
for p in range(n, 2 * n - 1):
limit += 1
min = 0
for i in range(limit, p - limit + 1):
j = p - i
if min == 0:
min = s[i][j]
elif min > s[i][j]:
min = s[i][j]
if p == (2 * n - 2):
string += str(min)
else:
string += str(min) + '->'
return string
原矩阵:

运行效果:
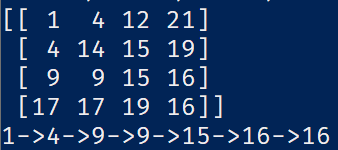
求矩阵最少(或最多)路径和(python实现)的更多相关文章
- 【python实例】要求输出字符串中最少一个最多八个的所有字符串组合(连续)
""" 题目:字符串str="ABCDEFGHIJK",要求输出最少一个最多八个的所有组合(向后连续字母) 输出如下: A [0::] AB ABC ...
- 市场清仓价格算法 python求矩阵不同行不同列元素和的最大值
问题描述 求矩阵不同行不同列元素和的最大值(最小值) 问题求解 1.通过scipy库求解 scipy.optimize库中的linear_sum_assignment方法可以求解 输入一个矩阵,参数m ...
- POJ 1151 Atlantis(经典的线段树扫描线,求矩阵面积并)
求矩阵的面积并 采用的是区间更新 #include <iostream> #include <stdio.h> #include <string.h> #inclu ...
- HDU 1828 / POJ 1177 Picture (线段树扫描线,求矩阵并的周长,经典题)
做这道题之前,建议先做POJ 1151 Atlantis,经典的扫描线求矩阵的面积并 参考连接: http://www.cnblogs.com/scau20110726/archive/2013/0 ...
- Comprehensive learning path – Data Science in Python深入学习路径-使用python数据中学习
http://blog.csdn.net/pipisorry/article/details/44245575 关于怎么学习python,并将python用于数据科学.数据分析.机器学习中的一篇非常好 ...
- MATLAB中求矩阵非零元的坐标
MATLAB中求矩阵非零元的坐标: 方法1: index=find(a); [i,j]=ind2sub(size(a),index); disp([i,j]) 方法2: [i,j]=find(a> ...
- POJ 1151 Atlantis 求矩阵面积并 扫描线 具体解释
题意: 给定n个矩阵的左下角和右上角坐标,求矩阵面积并(矩阵总是正放的,即与x轴y轴都平行) 思路: 扫描线裸题 http://www.cnblogs.com/fenshen371/p/3214092 ...
- 求矩阵中各列数字的和 Exercise08_01
import java.util.Scanner; /** * @author 冰樱梦 * 时间:2018年12月 * 题目:求矩阵中各列数字的和 * */ public class Exercise ...
- 求矩阵主对角线元素的和 Exercise08_02
import java.util.Scanner; /** * @author 冰樱梦 * 时间:2018年12月 * 题目:求矩阵主对角线元素的和 * */ public class Exercis ...
随机推荐
- Java为什么需要四种引用?
首先抛出一个问题:在闲暇时间收拾自己家里的时候,对某一件物件要不要丢弃的问题上,是否有过食之无味,弃之可惜的感觉? 同样的,JVM在回收Java对象的时候,是否对对象实例也有食之无味,弃之可惜的感受? ...
- C# 读取控制台的Console.Write
一个程序去调用另一个xxx.exe的时候,需要记录下这个exe里面的console.write的输出 public static string InvokeExcute(string Command) ...
- 关于javascript中的prototype
作为一个致力于前端开发的人员,能够熟练掌握javascript的原理和机制是每个小白的必经之路,这也是最痛苦的.有人说前端功力好不好最主要的就是看对js的掌握能力,有人说十年也啃不完一门javascr ...
- 【从刷面试题到构建知识体系】Java底层-synchronized锁-1
在技术论坛中,经常看到一种言论:面试造火箭,干活拧螺丝.我们平时写的大部分代码的确是CRDU,再提一个层次,也无非就是揉进去复杂一些的业务逻辑,把一堆的CRDU组合起来. 那么问题来了:我们提倡的研究 ...
- ASRWGAN: Wasserstein Generative Adversarial Network for Audio Super Resolution
ASEGAN:WGAN音频超分辨率 这篇文章并不具有权威性,因为没有发表,说不定是外国的某个大学的毕业设计,或者课程结束后的作业.或者实验报告. CS230: Deep Learning, Sprin ...
- css浮动产生和清除浮动的几种方式
浮动的语法:float:left/right; 浮动float的原本设计了作用初衷是为了实现文字环绕效果 浮动产生负作用: 1.背景不能显示 2.边框不能撑开父元素 3.margin padding设 ...
- 我的Java秋招面经大合集
阿里面经 阿里中间件研发面经 蚂蚁金服研发面经 岗位是研发工程师,直接找蚂蚁金服的大佬进行内推. 我参与了阿里巴巴中间件部门的提前批面试,一共经历了四次面试,拿到了口头offer. 然后我也参加了 ...
- python编程基础之三十六
文件处理:文件处理包括读文件,写文件 读文件: 1.打开文件 2.读取文件 3.关闭文件 写文件: 1.打开文件 2.写如文件 3.关闭文件 无论是读取文件还是写文件都时需要打开文件,和关闭文件 打开 ...
- MyBatis拦截器自定义分页插件实现
MyBaits是一个开源的优秀的持久层框架,SQL语句与代码分离,面向配置的编程,良好支持复杂数据映射,动态SQL;MyBatis 是支持定制化 SQL.存储过程以及高级映射的优秀的持久层框架.MyB ...
- Numpy数组解惑
参考: 理解numpy的rollaxis与swapaxes函数:https://blog.csdn.net/liaoyuecai/article/details/80193996 Numpy数组解惑: ...
