[算法模版]Tarjan爷爷的几种图论算法

[算法模版]Tarjan爷爷的几种图论算法

前言

Tarjan爷爷发明了很多图论算法，这些图论算法有很多相似之处（其中一个就是我都不会）。这里会对这三种算法进行简单介绍。

定义

强连通(strongly connected)： 在一个有向图\(G\)里，设两个点a, b 发现，由\(a\)有一条路可以走到\(b\)，由\(b\)又有一条路可以走到\(a\)，我们就叫这两个顶点（a,b）强连通。

强连通图： 如果 在一个有向图\(G\)中，每两个点都强连通，我们就叫这个图，强连通图。

分量：把一个向量分解成几个方向的向量的和，那些方向上的向量就叫做该向量（未分解前的向量）的分量。

强连通分量(strongly connected components/SCC)：在一个有向图G中，有一个子图，这个子图每2个点都满足强连通，我们就叫这个子图叫做强连通分量。

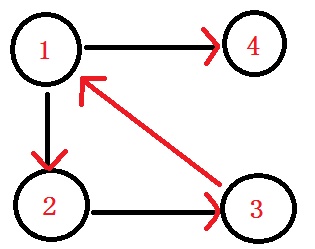
比如说这个图，在这个图中呢，点1与点2互相都有路径到达对方，所以它们强连通。

而在这个有向图中，点1 2 3组成的这个子图，是整个有向图中的强连通分量。

dfn[i]：指第\(i\)个点的\(dfs\)序。

low[i]：指第\(i\)个点的子树内的所有点通过反祖边能走到的点的\(dfn\)的最小值。

先行结论

• 在一个无向图上，跑一棵生成树。可以证明非树边只有反祖边，没有横叉边。

Tarjan算法求割点/割边（针对无向图）

割点

首先，一个比较显然的结论就是所有的叶子结点和根节点都不是割点。对于其他节点u来说，只要有至少一个儿子v满足low[u]>=dfn[v]，就证明v若不通过他父亲就回不去。那这个点就是割点。根节点只需要判断是不是有两棵子树就好了。实现起来可以当作有两个点满足low[u]>=dfn[b]。因为因为根节点\(dfn\)为1，所以一定满足条件。如果两个根结点儿子不通过根节点就能联通，那么他们一定在一个子树。

void tarjan(int now,int ff){
    low[now]=dfn[now]=++idx;
    for(int i=head[now];i;i=side[i].next){
        int v=side[i].v;
      	if(side[i].id==ff)continue;
        if(!dfn[v]){
            tarjan(v,side[i].id);
            low[now]=min(low[now],low[v]);
            if(low[v]>=dfn[now]){ans[now]++;}
        }
        else{
            low[now]=min(dfn[v],low[now]);
        }
    }
    return;
}
void output(){
	for(int i=1;i<=n;i++){
        if((ans[i]&&!root[i])||(ans[i]>=2&&root[i])){
            cout<<i<<' ';//输出所有割点
        }
    }
}

割边

和割点基本一样。只需要把\(low[v]>=dfn[u]\)改成\(low[v]>dfn[u]\)即可。同时需要判断，不能再次走刚刚走过的边。

如果点u的至少一个儿子v满足low[v]>dfn[u]。就证明不通过这条边无法走到上面。所以这是条割边。

Tarjan算法求点双/边双（针对无向图）

边双

和楼下的强连通分量很像，唯一的区别就是需要特殊判断一下，不能通过从父亲下来的那条边走上去。（因为强连通分量是有向图，走不上去，所以不存在这个问题）

实现起来也很简单，只用简单修改一下dfs函数：

dfs(u,f)其中u为当前节点，f为走到这个点通过的边的编号。

当在遍历u的所有边试图向下dfs时，只需要加一个if(现在准备选择的边的编号==f)continue;即可。

点双

咕咕咕

Tarjan算法求强连通分量（针对有向图）

stack<int> tp;
void dfs(int u)
{
    dfn[u]=low[u]=++cnt1;//初始化每个未访问过的节点
    tp.push(u);
    for(int i=head[u];i;i=side[i].next)
    {
        int v=side[i].v;
        if(!dfn[v])dfs(v),low[u]=min(low[u],low[v]);
        else if(!scc[v])low[u]=min(low[u],dfn[v]);//被访问过却没有SCC编号（在栈里），证明在同一个强连通分量。因为栈维护的是一条有一个节点到它儿子的路径。所以如果栈顶的点u到栈中任意一点v有边。就证明存在u到v的一个环。
    }
    if(dfn[u]==low[u])//如果这个点是它所在强连通分量中dfn最小的，则有它来承担输出整个SCC的任务
    {
        int s=tp.top(),id=++cnt2;tp.pop();
        scc[s]=id;
        while(s!=u)s=tp.top(),tp.pop(),scc[s]=id;
    }
}

参考资料

全网最!详!细!Tarjan算法讲解

割点和桥